zxy思维题乱做
有很大一部分来自于 zxy,课件等,一般都是很强的 Trick。
7和8月
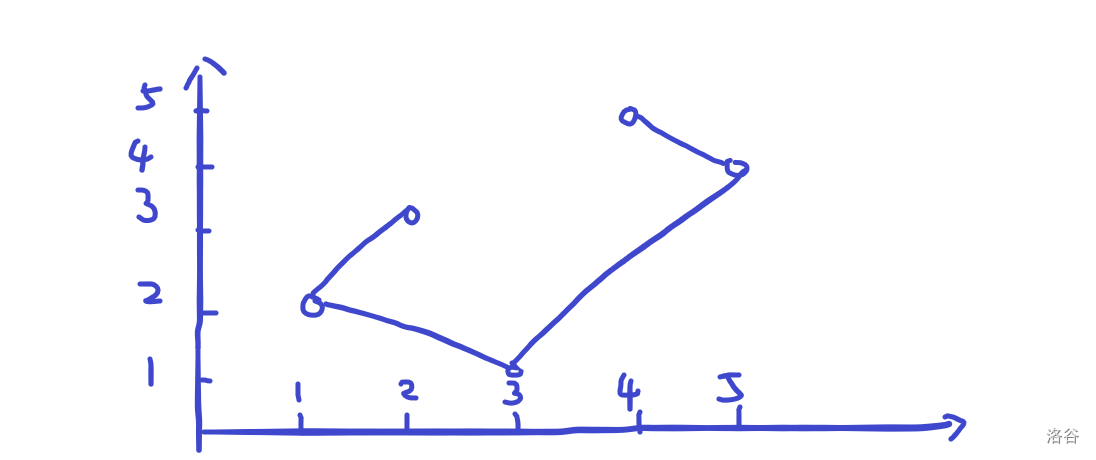
CF1476F
考虑 DP,设 表示前 个灯可以点亮的最长前缀,有转移:
- 朝右,若,则,若,则。
- 朝左:不难发现只要将前缀覆盖到 即可就行,设 为第一个 的位置,那么 的位置都可以朝右,那么,可以二分 加 ST 表查出。
反思:当我们要 DP 点覆盖的问题的时候,我们可以考虑覆盖一段前缀的形式。同时设计 DP 状态的时候一定要时刻考虑最小状态设计原则。
HDU6157 The Karting
权值是负的!不能贪心,直接 DP。
但是状态怎么设计呢?考虑记录路径,但是显然会算重一堆。我们可以只考虑断电,让后用前缀和记录回路的贡献。
用 DP 来处理端点,设 表示前 个点中,选出 个端点,其中从左往右的端点比从右往左的端点多了 个(),转移考虑当前点的贡献,一共四种情况:
- 不选这个点:;
- 选这个点但是只经过:;
- 选了这个点从左往右的端点:;
- 选了这个点从右往左的端点:$f(i,j,k)\leftarrow f(i-1,j-1,k+1) + a_0 + 2\times s_i $。
因为要走回去,那么答案就是,时间复杂度。
反思:对于匹配的问题,我们可以拆解贡献到匹配点,考虑到某一个匹配点时候带着贡献和需要匹配的记号转移,这样就能够保证转移的顺序性。
P6944 Gem Island
好题!
直接飞上去 DP 直接爆炸。考虑分析性质,首先这个过程过于庞大,我们可以分析末状态的性质。先看看对于一种最终状态 其发生的方案数,可以分为两个部分:
- 将 天分给 个人,钦定这 天是谁的手上的宝石数增加了:
- 对于每一天,计算当钦定的人手上宝石数增加的方案数,有:
不
那么我可以直接 DP 求方案数啦,但是问题在于我怎么求方案中前 大的 和呢?有一种 DP 方法,叫搭楼梯的 dp 方法。
通俗易懂的,我们要用 DP 维护下面的东西:
1 | *** |
设 表示当前最高的楼梯有 列,楼梯里头 * 的总数为 的方案数,上面这个东西就是 的一种方案。
转移很简单,考虑转移的时候在最高层加入一行,枚举这行里头有 个 *,让后从现有的 列里头选 列放到最左边,让后在这 行上面各加上一个 * 就是一种转移了。比如说上面的例子,枚举 的时候可以转移到,转移系数为,转移后的形态可以这么表示:
1 | ** <--- 新增的行 |
这种类似搭楼梯的逐层构造 DP,本质是对所有 “列高单调” 的状态等权枚举,将每一层的结构直接拆分贡献,凡是这类问题:
- 对象可以抽象为高度具有单调性的多列;
- 每一层的新增元素对目标量的贡献是可局部计算的(只依赖这一层的列数,而不依赖更复杂的全局信息)
那么我们就可以用这种转移做前 大(或小)的期望,总和,分布等。
回到本题,我们把宝石对应成 *,让后每一列对应一个人就可以啦。计算前 大的方案也就转化为了前 列的 * 的和,由于我们每次加入一行的那些列,不难观察出一定就是前 大的列,而且一次局部贡献只加入一个 *,所以可以直接计算。具体的,我们设 表示当前维护前 大,一共有 个宝石中所有方案数前 大的和,有转移:
其中 就是题目中所要的前 大。
答案就是。
反思:
对于这种多过程的题目,如果过程难以维护,我们可以考虑末状态有没有什么特殊性质。
学到了新的转移( •̀ ω •́ )y
哎我发现你过一段时间回来看这个题发现有些新的收获( •̀ ω •́ )y。
CF1442
想 DP,但是发现太难了耶。因为操作过于难了,并不是 DP 过于难了。
我们考虑如何简化这个问题,发掘以下性质。首先不难发现所有连在一起的同颜色的点可以一起删。也就是缩点。
让后怎么做?先从简单情况入手,把万能的灰点暂时禁言。让后考虑树是一条链的情况怎么做,因为没有灰点且已经缩点的情况下,这个链一定是黑白相见的,设链长为,那么答案就是,贪心策略是将出现次数较多的颜色删掉,让后剩下的连通块逐个删掉就可以了。
接着考虑树不是一条链的时候怎么做,发现上面的策略好像不太好去拓展,且有些情况下不是最优解。考虑再发掘一种策略,有一种策略:从最外层(度数为)把同色点一层一层删掉,设 为直径,那么次数就是。不难发现这个策略更优,可以用势能分析得出。
接着考虑有灰点的情况,问题可以转化为我们给每一个灰点选择一种颜色,使得再次所点后直径长度最短。这种情况需要我们进行 dp 了。设 表示 颜色为 的最长链, 表示 颜色为,经过 的最长路径,转移的时候把子树 合并上来:
,时间复杂度。
反思:在分析问题的时候,我们通过发掘性质让我们的 dp 有的放矢。从简单问题入手,一步步发掘真相,类似于侦探的过程,这种是常见的思维技巧。
CF1517F Reunion
直接统计十分困难,考虑转化问题,不难发现可以把问题转化为统计半径 的园的个数。但是如果你对这个进行计数 DP 的话你会发现这个极其容易算重,因为这个是存在问题。
我们考虑存在问题能不能转化为限制问题,这是计数问题中一个常用的思维技巧。不难转化为对于所有黑点周围 点的并集不是所有点,这个问题是一个染色问题,我们可以进行 dp。考虑状态中记录黑点往上覆盖的最远距离,或者是子树内最深的还没有被覆盖的点。这两个信息只有一个有效,因为如果子树内有没有被覆盖的点,设点 能覆盖这个点,那么点 的覆盖范围一定是子树内黑点往上覆盖范围的超集。
考虑设 表示子树 内, 则表明子树内黑点网上覆盖的最远距离是, 则表示子树内最深没被覆盖点的深度为,转移要分讨四种情况,时间复杂度。
反思:计数问题中所有限制问题优于存在限制问题。预计那这种会算重的存在性问题想一想能不能转化为限制性问题。
CF1368H1
一个显然的想法是建出来网络流的图,即 连蓝色接口,红色接口连,矩形内的所有点也建出来,向四周连容量为 的无向边,然后对原图跑最大流就是答案。
显然会炸掉,考虑不能跑最大流,那怎么办,利用最大流最小割定理,我们可以把原命题转化为求最小割,转化一下就是把矩阵的所有点染蓝或者染红(代表最后和起点还是和终点联通),求所有染色方案下的最小端点异色边数。
考虑 DP,发现直接 DP 没太大啥用。考虑发掘性质,我们发现如果考虑整张图都是红色的情况下,那么割就是蓝色点数,现在问欧体转化为我们要把矩形中一些点改成蓝色使得割最小。那么有一个想法就是改点一定要挨着边界,让后要改要么改一整行要么改一整列。
那么有结论:最优染色方案一定是一整行或一整列颜色相同。对行 DP,翻转矩阵后对列再 DP 就可以了,时间复杂度。
反思:从高复杂度算法开始,一步一步进行优化,这个和从简单问题推广到更难的问题一样。
最大流问题如果无法优化可以转化为最小割问题。手算最小割属于是一个常见套路。
acg009c
区间 DP,设 表示考虑到 个,第 划分到 A 或 B 的方案数。转移的话考虑 即可,但是要满足两个性质:
- 区间内部满足条件。
- 区间两端满足条件。
让后发现第一个的决策集合是一个 的一个后缀,第 2 个是一个前缀。用前缀和维护,第一个用分段 for 处理,第二个双指针。
CF573D
好题,但是田忌赛马。
有一个显然的想法就就是二分图带权最大匹配(或网络流),但是时间复杂度是 及其难受,考虑 DP 但直接 DP 十分困难,考虑发掘一些性质。
利用贪心思想,先对 和 进行从小到大的排序,一个基本思想就是对应位置的相乘,用调整法不难证明这是最优决策,但是本题目中存在第 个人不能骑自己的马,所以最优解可能不会取到。
考虑到这个限制只是限制自己不能骑自己的马,合理猜测 位置匹配马的决策是一个范围,有结论:匹配范围为。证明考虑反证法,设 的禁止匹配位置为。那么反证法,假设如果在这个以外的范围选,那么最多向前会造成两次 无法匹配,自行画图发现这种情况最劣情况下也只会在 的情况形成匹配。
借用 _sys 的图:
完美匹配至少有三个红线和黑线相交整法不难证明如果两条线相交那么交换这两个匹配会得到更优的解。
让后考虑交换的过程,我们如果前 个人和前 匹马匹配完全,那么存在,使得 这区间内的人和马匹配,可以用反证法证明。
故,设 表示前 个人和前 匹马完成匹配的最大全职,所以从 转移过来即可,同时改成矩阵方式维护 DP 做动态 DP 即可,时间复杂度,其中 是矩阵带来的常数。
反思:限制过松的题目,我们可以通过强化限制使得题目范围的解缩小,让题目简化。
AGC009E
我太拉了,还是看 大佬 的题解吧。
反思:在具有强烈过程性的题目可以往结果的方向猜性质,观察性质的时候可以观察操作是否具有什么特殊性质,例如本题的 叉树。
CF1481E 还有 abc201F
不难发现每本书最多移动一次,移动多次一定是不优的。
把每本书的状态定义为 0/1 表示移动或不移动,枚举这本书的状态,如果以最后一本不动书为界限,那么前面的书那么前面的书如果属于同一种类,那么一定同时移动或者同时不移动,否则这本不动书就会使他们不能相聚。
所以我们枚举最后一本不动书,它后面的数一定要动,现在要决策它前面的书,其实就是选出来书种类的区间不能相交,那设 表示前 本书中最大的不动书个数,预处理每本书左端点 和右端点 以及出现次数 就简单了。
反思:状态设计如果没有思路,可以尝试使用枚举法来设计状态,有助于思考。
同类型的题:abc201f
CF1474F
头脑风暴!
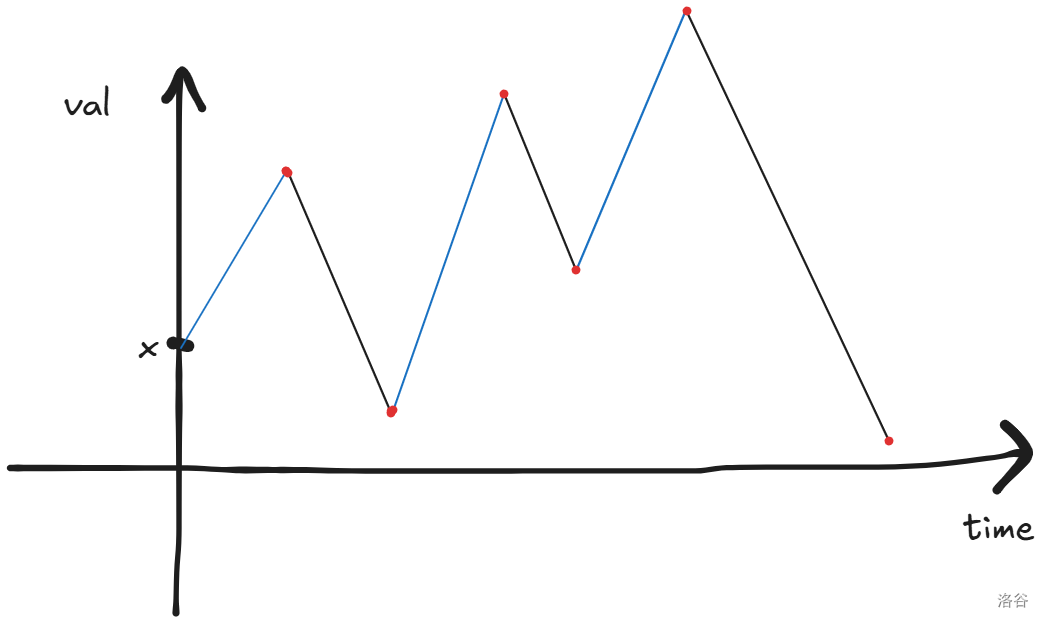
注意到 对答案一点用都没有,因为我们求的是长度,光一个 就能够确定答案了。
发现最长严格上升子序列的性质不太好刻画,我们考虑这个添加数的操作过程能不能以一种形式来表现出来。注意到每一个数具体取值只和最后一个数的变化有关,而且变化是连续的,考虑给它拍到二维平面上,横轴按照每一次添加一个数划分时间,纵轴为最后一个值的具体取值,原操作在二维平面上表现的是斜率为 1 或 -1 的一堆直线,如下图,红点表示一次插入操作的:
最长严格上升子序列的性质就很好刻画了,因为根据图来看其实就是最低点和最高点的极差就是我们的长度(因为斜率为)。让后我们考虑这个子序列个数怎么解决。发现直接 DP 求解答案十分困难,考虑发掘性质,首先不难发现一个性质:一个段不可能贡献超过一种答案,即一个点不可能成为最低点或最高点。
这个性质有什么用呢,也就是说,我们可以统计对段的答案进行贡献统计。然而注意到段数极小(数据范围),值域极大,有一个强烈的矩阵味道,但是我到现在连状态都没设计耶?
最长严格上升子序列可能从任意值拼过来,考虑在状态中加上这一个,设 表示目前计算到第 段,末尾值为 的方案数,哎这矩阵味道对了,转移:
矩阵快速幂优化,时间复杂度。
反思:状态设计中需要是可考虑当前状态能否刻画子问题,不要受限于定居思维。
CF1463F
容易发现以最优解应是以某一循环节重复多次的形式。
考虑对循环节求解,发现数 的躯体取值仅和前 个数的选取情况有关,注意到,考虑状压。因为循环节选取情况一样,所以我们只用遍历第一个循环节的数进行状压。
令,全集为。设 表示在第 个点,前 个数选取状态为 的最优解。
记 表示 不选的选取状态,那么有转移。
若选,则要满足 没有被选,那么有。
其中 表示 能产生的贡献,具体的:若,那么原串可以被分为多个长度为 的循环节,个数不妨设为 个,和最后的 的遗留串,不妨设长度为。
若,那么,反之则为,故可以直接做。
MLE 了记得滚动数组。
反思:若状态转移过大的时候,考虑找规律,矩阵快速幂,或者找循环节。
Cf1188D
题目要求的就是求:
其中 表示二进制位中 1 的个数,为了方便不妨令。
考虑如何求解这个式子,我们考虑按位规划,我们考虑以下信息:
- 在这一位规划的代价。
- 所有 在这一位的出现情况。
- 是否在之前的规划中出现过进位。
如果我们直接暴力状压进位的话,时间复杂度是,及其难受,但是,我们考虑到如果只保留前 位,越大的 约有可能进位,如果我们把所有 排序后,那么发现进位的一定是 的一个前缀。故设 表示考虑到第 位,有 个数发生仅为的最小代价,时间房租啊都。
反思:我们在 dp 优化过程中可以考虑只保留我们需要计算代价相关的状态,这是一个常见的 dp 优化方式。
CF1539E
首先答案可以抽象为 0/1 相间的串,进一步,可以把答案看作 0 一段,1 一段的串。
如果说,我们答案串里面有一串 0,区间在,那么这一段给出的每一个数一定满足:
考虑到操作对后续有影响,而对前面没有影响,考虑倒着确定每一个数,倒着扫。维护 0 一段 1 一段的合法区间,每扫一个位置看看上面第二个条件是否满足,如果可以就转移。对于转移是否合法可以用布尔加与运算维护。时间复杂度。
反思:对于答案是 01 交错的题目,要有把答案切成许多全 1 或全 0 串的思路。对于值要满足后面会出现的限制条件,可以考虑倒着扫。
CF375E
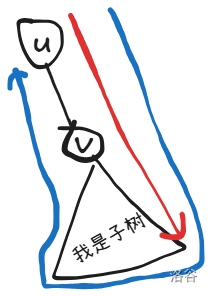
注意到红色位置没有一丁点用,而且交换操作是很难记录的。注意到黑点总数是固定的,而且交换时任意位置进行交换,不妨考虑让子树内钦定放了几个黑点。
但是这个转化还没有解决 的问题,可以满足子树内(不包括)的点满足条件,这么设计状态是可以的,但是如果包括 了就得直到谁给 产生贡献。如果第三维度加上距离 不好确定,因为贡献不唯一,但是如果我们钦定谁能解决 的问题的话那么问题就很好做了。
即,设 表示 子树内放 个黑点,用 点解决 点距离的问题。满足的最小代价。
转移考虑枚举第三维这个点具体是什么,从儿子合并上来,有分类讨论:
- 若儿子 第三维:那么有
- 若儿子 第三维:考虑到父亲肯定不会选儿子 子树内的点,孩子也不会选子树外的,证明可以考虑调整法。 那么我们合并完 之后直接找到对于每个 子树内 对应最小的 转移即可,时间复杂度。
反思:问题前后相互影响的时候,或者操作是全局的,可以尝试把操作部分定义到局部变量里面跟翻遍我们去处理。
卡空间,用 short 即可:
P5289 皮配
题面过于复杂,有一个显然的想法就是让导师们去找学生,设 表示四个导师选的人数状态下的方案数,转移判断满不满足题目中所给的派系和阵营限制即可,时间复杂度,不难发现只需要确定三个即可,时间复杂度。然后就不会了。
观察这个 DP 及其难以优化,因为如果我们缺任何一个信息都无法描述完整的子问题,而且复杂度要求的可是,你只知道一个信息那么肯定啥也导出不了啊。我们考虑发掘几个性质:
- 确定一个派系和一个阵营可以唯一确定一位导师。
- 题目中 ban 导师的相当于不选钦定的派系和阵营。
上述性质启示我们让每一个学生去确定它们的派系和阵营,而不是导师去确定学生。但是还有我们的 “坏” 学生,不喜欢选的。我们先丢掉它们,先考虑 的部分分。
有一个显然的 DP 就是 表示 个蓝阵营的人, 个鸭阵营的人的方案数,剩余两个可以由这两个状态唯一表示出来,时间复杂度,仍无法通过。正解启示,考虑进一步发掘性质:
- 题目中学生来自的城市限制,和学校限制是互相独立互不冲突的。
这个性质启发我们分离上面状态设计中的。那么不妨设 表示蓝阵营有 个人的方案数, 表示鸭阵营有 个人的方案数,两个答案可以通过乘法原理分别算出来之后乘起来即可,时间复杂度。
现在考虑,一个重要的观察是。状压、枚举?都不对。我们上面的计算答案过程中体现了乘法原理的思想,也就是说我们也可以分离 “坏学生” 和 “好学生”,好学生单独做,坏学生单独做,最后乘起来即可。
坏学生的限制怎么处理,我们肯定不能用 的算法了,这个算法肯定是无法处理我们的限制的。回看我们之前 的解法,这个就能够很好的处理性质,因为状态能够表示所有派系阵营选择人数,我们可以用这个算法处理坏学生就可以啦。时间复杂度做的话是 的。
那么时间复杂度就是。
总结:
- 我们在设计状态的时候,应当尽量个限制紧密贴合。在优化 DP 的时候我们要考虑我们计算贡献具体需要什么信息,我们需要什么信息就足够了,去掉冗余的无用信息。
- 题目可能会故意引导你走向死路,如果一个方向想不通,不妨正难则反或换一种方法想,这里体现的是正难则反的思路。
P7214 治疗计划
把未感染和感染抽象为 0/1,那么原问题可以转化为初始有一个全为 的序列,可以在特定时间进行一次区间覆盖操作(有代价), 会向左右扩散,问能不能将整个序列全部覆盖为 0 且使得操作代价最小。
对于选择区间进行覆盖的问题,这一类经典问题有一种状态设计就是设 表示将 这个前缀进行覆盖的最小代价。但是问题在于这样转移是 的不太好搞,考虑这个 的瓶颈就是在于我们需要知道每一个覆盖区间右端点在哪里。考虑切换一下 dp 状态,设 表示将 覆盖的最小代价,转移通过 的偏序关系进行转移:
时间复杂度还是,无敌了。而且还自带两个偏序关系更是逆天。但是观察这个 DP 是一个类似于最短路形式的转移(说人话就是转移代价只和目标的代价有关),考虑用 Dijkstra 优化这个 DP。让后绝对值可以通过对 排序去掉,对于转移可以用线段树优化这个最小值转移,势能分析有时间复杂度。
总结:
这个题目有一个巨大的卡阻就是在于 DP 容易选择会以时间作为主体,这样的话你无论怎么都无法优化掉时间这一维。一开始想的就是 添加了时间 这一个维度,但是发现这个枚举时间反而成为了瓶颈。这个时候,我们需要分析,我们知道什么就够了。分析下来 反而可以从转移中天然的去掉,这样我们就做到了优化 DP 的过程。
CF553E
考虑倒着 DP,设 表示第 个点走到,当前时间为 的期望。有转移:
末状态,
时间复杂度,无法通过,考虑优化,发现一堆优化板子都套不上去,但是发现 FFT 可以套上去。考虑 FFT 优化,但是注意到这个玩意差卷积不能卷因为这玩意是半在线的。考虑分治 FFT,但是对什么进行分治呢?考虑分析转移方程,注意到方程中时间的转移时具有顺序的,可以进行 CDQ。不妨对时间一维分治。
具体的,记 来表示,用,在分治底层计算出,时间复杂度。
好消息是又学会了一个科技。
反思:DP 优化不仅仅可以从状态优化和一类特殊的转移优化,也可以通过转移的顺序进行优化。
P3226 集合选数
纯纯构造题,首先 可以通过状压枚举子集做到,通过高位前缀和有。当然这都不是重点,问题是。
考虑分析性质,先简化问题,从只有 的性质。考虑转化模型,让 连边。那么分析图性质不难发现图形成了一条一条的链,那么原命题相当于在上面求解独立集。
接着考虑 的性质,让,发现图转化为了如下的形态:
那么不难发现图形成了网格图的结构,但原命题相当于还是在上面求解独立集问题。分析这个网格图,发现行数大约为,列数大约为,数量极小。考虑状压求解独立集即可。设 表示考虑到第 行,一行选取数状态为。预处理合法状态转移即可。
总结:
我们可以通过图论等模型来对题目性质进行进一步转化,同时从简单问题出发,一步一步添加限制也是一个思维角度,在添加限制的过程中会发现一些奇妙的性质。
CF830D
这玩意好像直接 DP 求发现我们无法确定这个转移顺序和 DP 主体,有可能是路径长度或者树本身。考虑从这个图发掘一些性质,手摸几个小深度的不难发现一些小性质(仅对正解有启示作用):
- 一定存在经过所有点的路径(即哈密顿路径),且路径起点终点一定是叶子,这个路径一定算入答案中。
- 树的两个孩子由 树构成,同理 两个孩子由 树构成 ,以此类推。
- 路径可以看作一条有向链。
由于仅对正解起启示作用,故不给详细证明。性质 1 的证明可以归纳法证明,由叶子到叶子的哈密顿路径可在每个父节点处用左右子树的哈密顿路径路递归拼接得到,因此总能存在经过所有顶点的简单路径。
同时结合性质 2,任一节点的子树在哈密顿路径中必须整体连续出现,且路径端点必是叶子,因此全局路径只能自底向上由叶子路径块依次合并成更大的块,否则无法覆盖所有组合且会漏算。启示我们 DP 的主体以树为主体而非路径长度,顺序为自底向上合并。
让后设 表示 树的贡献,但是发现合并贡献的时候不知道信息,考虑添加一维 表示有 条路径链的方案数。转移如下:
时间复杂度。
总结:
DP 顺序和方案顺序是不一样的,这道题通过类似于自底向上的合并顺序将若干条(有向)路径合并到一起。
有的时候不好确定 DP 主体和顺序的时候,可以考虑发掘一些小性质,通过小性质将不合法的转移顺序排除。
路径问题可以看作几个有向链的合并过程。
gym102538H
这道题和上面一样,也是路径计数问题并且考虑的是有向链的合并过程。
首先考虑转移顺序,分析性质发现:
- 成环的部分一定是 所覆盖的。
- 环可以拆成两个有向链。
考虑 DP,首先对 排序从小到大覆盖区间,简化问题。每次增量一个左部的点,然后考虑它连出去的两条边,达到的效果就是合并两条路径。
设 表示当前考虑前 个点,形成了 条路径,转移有两个:
- 添加 个右部单点:。
- 取两条路径合并:。
时间复杂度。
总结:上面两道题给我们了对路径计数问题的一种新看法:有向链的分散与合并。DP 的顺序和方案顺序可能并不一致。
CF235D
首先很难发现这玩意就是让你求概率而并非期望,因为递归次数可以分配到每个点上,权值为 1,所以答案就是概率求和。
让后考虑概率怎么求,先定义概率是什么,我们发现如果一个点 要想给另一个点 组合,即选取点 为点分治中心,中心与 联通的概率。贡献的话,那么必须要保证 的路径上必须没有点被删,即 是第一个被删的。大胆猜想概率就是,考虑证明用归纳法证明:
- 若直接删除,概率就是。
- 若没有删除,那么贡献必须保证删除点之后 联通。删除一个点的概率为,子图内概率为,故这种情况概率是
不难发现加起来就是,暴力枚举点对时间复杂度。
考虑放到基环树上怎么做,发现这个 会出现环上两个路径的问题,概率上这两个路径的权重是等价的。考虑如何同时统计两个环上路径的概率,发现很难统计会算重。正难则反,考虑不遍历环,我们直接容斥,设两个路径长度分别为,令 到自己树根的距离为,那么容斥就是,即多算了两个路径都联通的贡献,时间复杂度。
总结:
合理利用期望的线性性,要分清是求期望还是概率,别一上去发现求的是概率就搞笑了。
从简单往难推是一个合理的思考思路。
CF1608F
有一个显然的想法就是状压所有我们选过的数,发现时间复杂度是,及其难泵,考虑分析 mex 运算的性质。
- 当前 选的数比 mex 大,mex 取值不变,同理选的小,不过我们不考虑小的情况从小到大选。
- 每个位置 mex 的取值是具有限制的。是一个值域范围。
我们考虑我们的状态设计,我么需要在规划完前缀 的时候得到它的 mex,也就是我们的状态必须有这两个维度。除此之外我们还需要所有大于 mex 的值才能让我们转移 mex,但是这不又回到了状压了吗?
我们考虑寻找大于 mex 的等价性,如果我们在一个数对 mex 产生贡献的时候再去计算的话就可以啦。设,表示目前到第 个,大于 mex 的数为 个,但是我们未确定这些数,mex 为 的方案数。
- ,对 不会造成影响:
- ,对 不会造成影响,但是要考虑它是归入已有的未确定的值中:
;
还是新增一种未确定的值: - ,我们改变 变成(),那么需要用卡未确定的值来填补 的这一段,
方案数就是排列数
时间复杂度,考虑优化,我们把最后一种转移优化一下,把状态偏移:,最后一种转移可以对第三维做前缀和,其他转移同下:
时间复杂度。
总结:
- 能需要根据限制的特性,提前或延迟确定一些元素的过程。
HDU 6566
有一个 表示 子树内权重和为,当前点选不选的最大权值。时间复杂度 无法通过。考虑优化,我们用 dfs 序转移来进行优化,但是发现 dfs 序从 的时候进行转移,若 对应的节点在 对应的节点的上方时,就可能不知道 选取的情况,而且暴力状压是不行的。
发掘性质,dfn 相邻的点的移动轨迹一定是往上跳若干步然后往下走一步(这个性质很有用),官方题解告诉我们先进行轻重链剖分 然后划定 dfs 序的时候最后遍历重儿子 这样你在 的时候会直接跳过上面的一段重链,我们发现对于每个点只需要记录每个重链的链底就好了,由轻重子树剖分性质不难有状压状态数为。
设 表示考虑到 dfn 为 的点,当前根的链底的点状态为,已经用了容量为,转移可以写成,时间复杂度。
反思:头一次见树形 DP 还可以转到 DFS 序上进行操作,属于是切换了转移顺序。发现就是如果你切换转移顺序可以利用切换至后带来的特殊性质,使得状态是可以减小。
P7213
这题真是无敌了,想 30 分钟结果连状态都没设出来。
直接 DP 发现没有什么好玩意,考虑发掘一些性质,发现性质是真 dmt 的难找:
- 序列 A 所代表的末状态 所构成的集合其取值一定是一个 的排列。
- 震柱子从 2 到 1 一定是值域从大到小震。
- 操作造成贡献是对值域上位置最靠后的值操作。
由上面三个操作可以一个操作的导出:从值域上从大到小,我们将两个位置位置靠前的减。发现这个没有什么前途因为我试了 www。
考虑性质都是从位置靠后的值操作,有一个操作直接导出就是位置从后往前扫,维护当前值最后一个出现的位置,如果没有出现过,就维护不变,否则减 1。
让后发现每一次都要执行这个操作,如何做到 而不是 操作,发现如果当前柱子之后有高度为 的柱子各一根,那么当前柱子及之前的柱子,如果高度 ,都会被直接震没。
发现这个玩意及其有用,我们考虑在这个上面 DP,借鉴 CF1608F 的思路,设 表示进行到第 个,取出集合最大值为 的方案数。
方便转移,我们需要设定几个参数:
- :表示后 钦定消失的数量。
- :表示后 钦定存在的数量。
此外需要区分一下同样高度的两个柱子(比如染色)以便转移,最终答案就需要除掉 。
分类讨论:
- 如果 钦定消失,那么 不变,从 转移,此时有 个可用高度,而 个给了取出集合,还有 个已经钦定,那么系数就是。
- 如果 钦定保留,我们同样考虑它的 取值:
- 如果,我们只能稍后进行确定,从 转移系数为 1。
- 若,有些标准柱的高度还未确定,所以我们需要考虑接起来之后的高度阈值。我们枚举一个最大值,此时从,计算系数有:
- 选定位置。
- 确定当前长度。
- 考虑 的形成方案数,令其为。
乘起来即可。
现在考虑 的转移,我们枚举最后产生的高度,那么有:
- 和,显然不会互相产生影响。这部分的系数为。
- 和,排列总方案数。
- 考虑 的方案数,共 个高度可以选择,但是 已经被选了,所以还剩下 种方案。
转移乘起来即可,时间复杂度。
总结:
这个题实在是太复杂了,即运用到 CF1608F 的延后确定值的思想,又有许多的特殊性质,这个题提取出的精华就是这种延后确定值和钦定值的思想。
P2048 [NOI2010] 超级钢琴
不难发现答案要求的就是前 大。
先考虑 如何做,有一种做法先前缀和,让后固定左端点,那么其对应的右端点区间就是,用 ST 表查这个区间对应的最大值前缀和就可以取到多大就可以了。对每一个 做一遍时间复杂度是,瓶颈在 ST 表预处理。
接着考虑 如何做,考虑求前 大的一个经典技巧:用堆维护状态,但要保证堆内情况能做到不重不漏遍历所有情况。
发现每一个左端点对应唯一一个大根堆(以前缀和权值)笛卡尔树,我们可以考虑类似于遍历笛卡尔树的过程进行操作。具体的,先遍历所有,都做一遍 的操作,让后设定状态 表示左端点在,管辖区间为,当前状态点最大权值为,决策取在 这个右端点。把所有左端点的答案丢进以 决策的大根堆,让后取出堆顶,记录答案,让后类似笛卡尔树一样,把这个以 劈开成,重新求 加入堆里面,重复做 次即可。
大部分题解的做法可以归类到笛卡尔树的结构,但是我在课上说这个大概是一车人没听懂。
总结:前 大/小 的权值可以通过用堆来维护状态,但是我们在用堆来进行维护的时候要做到不重不漏的遍历所有情况,状态的设计是一个重要思路。
CF1060F Shrinking Tree
这题状态涉及真有点巧妙和困难吧?
直接飞上去树形 DP,发现坠机了。考虑发掘一些性质能够,首先规划一个复杂度目标是。
- 根不固定,答案一定和子树大小有关。
- 进行边缩点操作,不妨最后得到的点为,那么 的儿子会全部接到,产生新的限制。
- 操作是全局的,如果我们无法确定子问题操作顺序的话我们无法确定合理的 DP 顺序。
先确定 DP 主体,我们要对断边的顺序进行概率 DP,将这些概率求和之后除掉 就可以啦。
让后解决性质带来的问题,对于第一个性质(问题)的解决,我们可以考虑通过枚举法枚举树根给他固定下来,让后钦定这个点是我们最后缩点剩下的点,让后在进行 DP。
发现第二个性质和第三个性质是绑定在一起的,因为如果我们不知道操作顺序的话我们也无法知道缩点之后产生了多少新的限制。先考虑第二个性质,断边之后会带来新的限制,我们可以规划到 的子问题,就是单独考虑 的时候这些边不能让 被消掉。
而对于第三个性质,有一个 Trick:全局操作可以将操作设进局部状态内。具体的,这里的新限制一定是在删除 这条边之后产生的,我们状态中需要记录操作的时刻。设 表示 子树内,删除顺序中后 条边不让 点被消掉的概率。同时记 表示只考虑子树 和边 的概率。
转移考虑枚举 断开的时间:
- 若:那么我们必须要乘上 的概率,后面的 条边需要改接到 上。转移就是。
- 若,那么 和我们没关系,这条边会提前断开,但是仍然需要考虑那些改接到 上的边,所以。
求出辅助 之后我们可以背包得到新的。因为我们还需要规划断边的顺序,而子树间的断边是互不影响的,所以可以直接用组合数计算方案数,保证考虑到的边和没考虑到的边之间的顺序即可:
答案就是,时间复杂度,优化是前缀和优化。
总结:
全局操作可以通过转化例如本题的记录时间转化到局部状态内部。
对于变量我们可以通过枚举法帮助我们进行决策,同时寻找状态之间的不动点。
寻找子问题最重要的是找状态之间的相似性,所谓相似性的含义就是信息记录在子问题中的一部分的占比,本题目中我们通过构造不动色这一相似性来让我们的子问题可以刻画。
WC2022杂题选讲 stars
为什么我搜不到题啊?
一颗星星可以抽象成 维空间中的一个整点。称若干星星构成的集合 是奇妙的,当且仅当在 维空间中的整点, 与 中的每颗星星存在至少有一维坐标相同。
有一个长度为 的星星序列,请你求出所有奇妙子区间的个数之和。
触发敏感词 “存在”,联想到 CF1517F 战败经历直接哈气转限制问题。首先 很小,可以暴力枚举法来确定我们坐标的相同的限制。
有了这个思路,我们来判断 中集合是否是奇妙的。我们首先把 拿出来,暴力枚举我们钦定的第一个相同的位置。让后接着往后遍历,遇到一个不符合相同的,就在暴力枚举一个,一直往后做直到方案可行即可。
发现上述的过程就是在枚举一个 的排列,按照这个排列钦定即可(也可以不用全部都用),让后我们要把他搬到计数上,首先发现排列数级别在,数量 120 极小,可以直接加进 DP 状态内。
倒着扫更方便我们处理,设 表示我们扫到第 个,钦定顺序为 的情况下,最远能拓展的距离。发现直接转移是十分困难的。
写出转移需要强大的观察能力,我们可以观察子问题之间的相似性来进行转移,我们考虑 和,其中 为去掉 的排列。只是对于 第一个需要新增元素但是可以被 解决的位置是不需要新增的,我们可以让 去解决,所以我们把 插入到当前最后一个锦囊的下一个位置就得到了 的等效子问题,也就是对于以后的影响都等效地传递下去了。
时间复杂度。
总结:
发现之前 DP 的做法顺序有一定的问题,我自己在做 DP 的问题在发掘完性质后就直接开始设置状态,我们在这些过程中融入了一个看似缺失的步骤:寻找子问题。
状态是对子问题的抽象描述,而子问题是状态所对应的具体计算问题。
为什么说是抽象地描述,前面我们所一直重复提及的 “最优最简状态” 的状态优化,就是在设出状态后要通过一系列的抽象化将状态变得简洁且更易计算。而我们状态的抽象化的前提是你的抽象化能够完整导出整个子问题才可以。
那么如何刻画子问题,需要把已经被当前处理的影响“消除”或封装好,让子问题状态只包含“未来的必需信息”,不受当前操作遗留的后效影响。我们将其简称为:“消除后效性”。
而寻找子问题最重要的是找状态之间的相似性。所谓相似性的含义就是信息记录在子问题中的一部分的占比,相似性越大你写转移就越容易,换句话说就是两个状态在未来计算中共享的“信息/行为”比例。
意义在于:高相似性可以让转移方程更统一、简洁,相似性越大你写转移就越容易,而低相似性转移方程复杂、需要处理很多特例。这也就是为什么转移方程有的时候及其难写,根本原因就是在于相似性程度低,状态太细,信息的共性没有利用,未来影响无法统一处理。
这需要强大的观察力和性质分析来分析这个相似性。
回到本题,为什么我们无法写出来转移方程,因为我们没有发现相似性。等效子问题就是一个关键相似性,等效子问题把复杂的状态差异“折叠”掉,只保留对未来影响的核心信息。
于是可以总结一个关键操作:当某个元素的决策影响很远,但 DP 每次只能一步更新时,通过找到一个当前问题的等效子问题,可以把这个远程影响一次性传递给下一步,实现高效转移。
求"满足某种条件的子串/子序列"的长度和、个数。
若无思路可以先考虑如何判断合法,再试图通过 DP 求得答案。
收获的地方就是在于遇到转移方程难写的时候,我究竟应该干什么了。还有等效子问题的优化方法。
CF1439D INOI Final Contests
我们是对 进行计数,发现没有空位的情况下是十分好做的,思路就是把人分配到空位置里。但是有空位的情况下就不太好做了,但是借鉴之前的思路,将位置分配给人。
设 表示考虑 个位置, 个人情况下的贡献,同时需要方案数方便进行转移,设为,定义同前。转移考虑分类讨论,有两种情况: 和。即有空位和无空位:
- :有一个想法就是我们可以通过空位划分子问题,考虑边缘的空位是限制最小的,枚举空位,划分为 和 的子问题。有转移:
- :这个时候就不能套用上面的做法,但是我们枚举最后一个人的最终位置,同时通过这个划分为两个子问题,令,有:
时间复杂度。
总结:
这道题就是枚举法划分子问题的巅峰神作之一,总和运用枚举法划分子问题。本题目就是通过限制设置分界线,将一个子问题划分为两个子问题,最后是转移的时候选限制最小的方式转移。突然发现枚举最大值 DP 这玩意和这个极其类似,通过枚举最大值划分子问题。
CF461E Appleman and a Game
神仙题,不是思路神仙,而是带来的收获很神仙。
先考虑我们直到 的情况下如何求最小,一个显然的想法就是建出 SAM,让后把 丢到 匹配,如果新加入字符使得当前状态不是子串,直接回到根节点,让后添加 1 的操作(SAM 能表示 的所有子串)。
让后我们对 计数,当然也可以这么做,设 表示当前进行到第 个字符,SAM 自动机状态在 的最小方案数。转移枚举新插入的字符,让后考虑状态 的变化。时间复杂度 直接爆炸,考虑优化。
发现及其难以优化,因为这玩意瓶颈就是在于枚举字符了,于是,我们使用刚刚学到的新技巧:“大步小步转移”
那么什么是大步小步转移呢?
- 小步:每次转移只做最细粒度的一步,比如一次只加一个字符、只处理一个元素、只走一步图边。小步适于考虑转移,但是可能会消耗更多时间
- 大步:一次转移跨过多步,把若干个“小步”打包成一个“段”直接跳过去。例如矩阵快速幂,倍增优化 DP。大步常常会很复杂,但是可能起到加速的效果。
我们尝试增大转移跨度,我们考虑操作次数为 的时候,能解决长度 以内的所有字符串,这个 最大时多少。
我们发现这个玩意毕竟和原命题不太类似,但是我们可以通过二分答案,若 则 合法,最后的答案就是。
虑这个新问题怎么设计状态,一次操作对应着一段字符串,要满足相邻两个字符串之间不能产生 的子串,充要条件就是前面一个字符串在末尾添加上下一个字符串的第一个字符不能是 的子串。
这说明我们只需要记录开头一段的第一个字符,设 表示 次操作,开头段的第一个字符是。能构造出来的字符串最短时,设 表示字符 开头,末尾为 之后就不再是子串 的最短子串。那么转移拼一段上去:
通过矩阵快速幂加倍增二分可以做到。
总结:
移的大步小步。小步适于考虑转移,但是可能会消耗更多时间;大步常常会很复杂,但是可能起到加速的效果。我们经常先用小步确定规则,再用大步优化效率。在大步小步之间切换,才能写出合适的转移。
CF559E Gerald and Path
wc,这题 3 个解法简直就是层层递进,一步一步接近真相。
这题完全有必要我单独写一篇题解。
解法 1
我们发现这个线段既可以向左延申,也可以向右延申。但是有一个问题就是重复被覆盖的,我们不能把他计入贡献,例如下面三种情况:
- 两个线段 不交。
- 线段 只交一部分。
- 把 完全包含。
由于这道题覆盖多次只计入单次贡献,所以转移顺序不能混乱。
先把状态设出来,发现长度延申只和处于最右端的线段决策有关,故设 表示前 个线段,右端点最靠右的线段是,朝向为左或右,所得到的最大覆盖长度。
考虑转移,转移我们要从状态向后拓展,考虑下一个产生贡献的线段,新增的贡献长度为(它最多能延伸自己长度,但若它和前面线段有重叠,只能算到不重叠的部分)而中间线段 的处理,如果这些线段如果完全在 的范围内,我们钦定它们方向让它们被覆盖,相当于忽略它们的贡献。 ——这步是本题的关键:否则你会担心“是不是算少了”。但实际上算少不会影响正确性,因为最优解一定会被统计到;而乱算反而会导致重复覆盖。
转移时间复杂度。
总结:思考转移顺序是十分重要的,在覆盖 / DP 问题里,很多时候覆盖多次只算一次,或 顺序影响贡献。如果顺序乱了反而会把贡献重复统计,所以要设计合适的转移顺序。
忽略思想是转移顺序中的一个重要一环,同时也可以将一些不优解算入答案,只要不影响最终答案即可。
解法 2
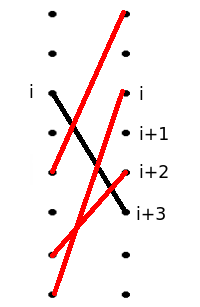
大家还记得 Lantern 把,那么覆盖一段前缀的设计。
这里我们先把 这些位置都离散化,考虑最终点亮的情况一定是若干个不交的段。转移的关键就变成了判定段是否合法,用 Lantern 的方法求出 表示用点 之间的线段是否能够覆盖 这些点,用 表示前 个点的答案,有转移:
转移条件 为真,时间复杂度。
总结:思考最后答案的形式,可能会帮助你把最优化问题转化为判定问题。寻找子问题要考虑消除后面操作的影响。
解法 3
既然覆盖条件不好求,正难则反,直接计算不被覆盖的区间付出代价,现在目标变为用尽量少的“代价边”覆盖所有点。
设 表示用前 个点的线段覆盖前缀长度 的最小代价。
如果线段向右覆盖:
如果线段向左覆盖,需要加一个 表示第 条线段向左倒。通过前缀最小值优化转移。
另外还要加上使用“代价边”的情况:
时间复杂度。
【UER #6】逃跑
答案求的是,可以写作,用线性性拆括号即可做到,这个 就是我们新经过的点数,而 表示两两配对。
考虑预处理 表示过了 的时间走到 的期望,可以 简单递推,这个玩意是基础我们先求才能地推出其他东西。同时令。
考虑求解 需要我们求单点对期望的贡献,而且是对每个时间都要求值,考虑设 表示第 时间新经过 的期望求和,有转移:
而 就是:
接着考虑,我们要处理点对之间的贡献,设 表示时间 内对所有坐标 的方案数,转移考虑容斥原理,总的方案数是先第一次走到 ,然后任意走到 。需要减去经过 的方案和完成目标后在原地打转的方案。总转移方程:
因为我们按照顺序计算的贡献,直接求和求出来的是,那么求答案可以这么写:
总结:正难则反是一个重要的技巧,通过正难则反,减去的东西就规约到了子问题。
而本题状态定义相当于将等价类定义到了状态中,大大减少了不必要的状态,这是因为它们的总方案易于计算,而容斥的方式是本质相同的,最后的答案也只需要求和,所以可以压缩在一起。这种涉及等价类的状态我们可以学习,这一类题也同样在皮配出现,寻找等价类是就是找它们的共同点。
P1721 [NOI2016] 国王饮水记
直接 DP 发现不会转移难泵了。
考虑发掘性质:
- 不会贡献答案,显然可以去掉不会影响答案。
- 一个水站最多会被除 之外合并一次。
- 若操作次数管够,一定是将 从小到大,一个一个和 进行操作。
我们发现第三个性质很 ok 啊,我们考虑给它拓展有拓展次数的情况,那么我们观察样例解释发现他们会通过把一些数取平均数后,然后和 整体操作。
那么就好说了,我们有一个策略,就是如果有操作次数的情况下,我们将这个 从小到大,让后我们将它们划分为几段,让后我们一个一个和 进行操作。这其中要满足段数单调不增。
现在可以 DP 了,设 表示进行到前 个,划分了 段, 的最大取值。转移枚举下一个划段:
转移是,可以通过前缀和优化,设,有:
时间复杂度,考虑优化,这个分式有点奇怪,考虑变形:
这是一个不是很典型斜率优化,考虑把转移的含义看成最大化斜率。具体的,平面有一堆 的转移点,要求 到选定转移点连成直线的斜率最大。
我们要维护的是转移点的下凸包,可以用单调队列优化至。
最后的分数需要发现非 的段只有 个,也就是说我们只需要 dp 大概 14 层即可,后面的的拿单个补齐,层数很少的时候 dp 可以直接用 double,让后得到转移点之后用高精度计算即可,时间复杂度。
总结:这种是不常见的斜率优化式子,是要求我们变形出斜率的形式,来去维护凸包。
2025牛客多校第一场(模拟赛T2)
分析性质,发现这个切割可以看作一个树形结构,将区间树选择一个地方劈开,让后会分裂为左右子树,而左右子树也可以继续递归直到叶子,而叶子我们是直到答案的就是 0。启示我们进行类似于区间 dp 的操作
设 表示将 整段切开的最小代价,设 表示 切第一刀的决策点在哪里,转移枚举分界点通过 转移满足限制即可,时间复杂度。
很遗憾,这是错的,只有 20 分,为什么?因为我们的状态无法满足题目的限制,放到树上相当于就是父节点的不平衡值大于等于子区间所有不平衡值,但是我们 DP 在计算过程中低代价方案可能被剪掉(即本来有代价更大,但是满足限制但是因为 DP 没有记录导致错误),导致有解的方案输出无解。
故设 表示 但是分割点在 的阈值 和最小代价(二元组)。
转移考虑先枚举切点,左右和,那么不平衡度就是,代价就是。
转移即为:
其中 表示一个函数,支持查询区间 能在最大不平衡 的条件下实现的最小总代价。可以通过前缀 加二分实现。
时间复杂度。
总结:
在设计状态的时候,要考虑情况完全,要保证设计的状态能够导出整个子问题。本题错点不再子问题寻找,而是在于状态的设计出了锅。以后 DP 转移一定要列全,跟着 OI BIG Trick 的步骤一步一步做。
P11085 [ROI 2019] 学生座位
考虑发掘性质:
将学生按升高排序之后相邻两个配对最优。
把课桌升序排序之后按顺序分给学生最优。
性质 2 是很有用的,但是后面再说。
既然这么说了,我们可以把 组同学相邻同学绑到一起,一共一组最多 块。而计算课桌的代价的时候因为课桌升序排序之后按顺序分给学生最优,可以通过单调性双指针,时间复杂度,无法通过。
我们没有很好的利用单调性,第二个代表决策单调性,每次求第 的最优匹配点,然后左右的决策点范围是,用 CDQ 分治容易有。
CF1562E Rescue Niwen!
2500* 没做出来。
考虑最长上升子序列有什么性质,遥想当年 DIV3 模拟赛 LIS 的一个解法:维护末尾元素的转移。这里我们同样的,维护结尾子串的转移。但是还不能进行 DP,考虑发掘性质:
- 对于子串,字典序大小有。也就是说一旦选取,那么 一定会被选。证明考虑反证法,我证明了 5 万年。
这个性质很有用,考虑直接对末尾进行 DP,设 表示结尾为 的子串的最长上升子序列,转移考虑枚举新后缀,求它们之间的最长公共前缀,只要 即可转移,转移方程如下:
时间复杂度。
总结:
考虑有效状态又多了一种思路:只求出跟答案相关的 dp 值即可,只用于转移的 dp 值可以考虑其性质。
CF708E Student’s Camp
这个题好像每太那么多的性质,那么直接 DP 发掘性质吧。设 表示 天过去了,第 行, 还在的概率。但是我们发现我们都钦定第 行谁还联通,不如大胆一点,直接把天数去掉!设 表示第 行, 还在并且前 行还联通的概率。
然后考虑转移,发现转移有些困难,但是在这之前我们需要预处理一个玩意 表示一行掉了 个格子的概率,这个玩意可以 做:
然后回到主题转移,发现转移时真的困难,因为转移的时候我们需要保证 连通,正难则反,考虑容斥减去不连通的方案数。
不难后面的东西可以前缀和优化,令:
优化即可时间复杂度,然后就不会优化了。
事实上当然是可以的啦,考虑后面的求和式子,一个关键观察式子只和求和有关而没有其他的式子,考虑以这个突破口,考虑到答案只需要整体求和,我们可以把状态也定义成和式。设,考虑写出这个和式的转移:
把 有关的部分提出来有:
用前缀和维护 和 即可,而 的计算可以用对称性用 计算,这是因为左右是等价的,所以翻折之后对应的值是相等的。
时间复杂度。
总结:
这里给出了 DP 的一种的新的优化方式,如果 DP 式子只和求和有关,我们可以将状态定义为和式来进行计算。
ARC160FCount Sorted Arrays
邦邦卡邦!学会了新的排列双射方式!
一个新的排列双射方式就是将排列 拆成 个 0/1 串,其中,那么 与 构成双射。而一个排列合法当且仅当分成的每个 01 序列最后操作完都是有序的。
同时分析题目的操作,因为逆序对数最多是 个,所以交换最多也只能是 级别的。
我们回到这题,我们考虑让,其中 从 一次下降,每降一次阈值,就恰好有一个位置(值等于当前的)从 0 变成 1。因此得到的 01 串序列是:
- 起点:全 0(可以看作)
- 每一步把某个坐标从 0 翻到 1
- 终点:全 1()
这正是一条在 上 “只增不减” 的单调路径。
并且“哪一个坐标在第 步被翻到 1”,恰好是“值为第 大的元素所在的位置”。
故每个排列对应一条唯一的单调路径,双射成功!问题转化为格路计数问题!时间复杂度,同时操作数是 级别的也是可以特判的,只有存在至少一个 01 排序后还有 时 操作才是有必要的。
更新操作必要性状态即可,时间复杂度。
总结:
计数问题当我们无从下手,我们可以借助一些已有的知识与原命题构成双射。简化问题。
CF1387B2 Village (Maximum)
发现这个就是点之间进行配对,有一个 Trick 就是将点对之间贡献分摊到边的贡献上。我们考虑边的贡献,也即是这条边究竟被经过了多少次,这个次数有一个显然的上界就是,其中 表示子树大小。
考虑如何构造使得经过次数最大,考虑式子 与取 有关,也就是说我们应当尽量让这个 大。考虑这个 上界是多少,有 不难证明 上界就是。这个上界什么时候取到,当然就是在树的重心。
考虑以树的重心为根,下面挂的子树大小都不超过。那么子树里面的点贪心策略一定是跨子树配对,故我们可以将所有节点按照 DFS 序后,第 个节点配对 个节点即可在另一个子树配对,时间复杂度。
总结:这道题的一个小 Trick 的就是将点对贡献分摊到边上,同时我们在最大化链的长度的时候要尽量跨子树。同时这个循环移位配对也是很好的思想。
CF516D Drazil and Morning Exercise
首先我们分析 怎么求,不难想到这个 一定和直径有关,那么 其实就是到直径两点中最长距离的那一个,证明利用直径为最长链的性质即可证明。
然后考虑 怎么做,有一个显然的想法就是暴力枚举最小值,固定的点,让后从这个最小值的点向外进行拓展,直到拓展到 的限制。
然后考虑如何优化这一过程,我们发现瓶颈首先在于枚举最小值,考虑优化这一步骤,我们发现最小的 一定在直径上取到,考虑直径上取 的点为根作为树。这个树有一个性质就是从当前点往下走, 单调不降。也就是说从该点到祖先的链上 具有单调性,我们可以在遍历这个树的时候维护祖先链,然后二分查找连通块大小即可,这个玩意直接做还是,通过树上差分有。
总结:树上最远点问题可以转直径端点
CF1622F Quadratic Set
平方数没看懂,换成完全平方数就看懂了。连夜将 OI BIG TRICK 中的完全平方数的性质改为平方数的性质。
性质:
- ,也就是说 不同奇偶的时候是一个完全平方数。
- 打表发现答案下界为?
我们考虑这个连乘阶乘能否分析:
后面是完全平方数,考虑前面的式子。
- 当 为偶数,也就是说。
- 当 为偶数,构造考虑将 去掉即可。
- 当 为奇数,构造将 去掉即可。
- 当 为奇数,把 去掉就可以变成上一种情况。
然后考虑完全平方数的性质如何满足,注意到完全平方数的本质就是质因数上次数都为偶数,注意到我们只关心就行即可,我们考虑异或哈希,设 表示 的哈希函数,若 为质数则随机赋权,反之为质因数异或和。然后利用异或哈希模拟上述过程即可,时间复杂度。
总结:
当性质不好发现的时候,考虑打表发掘性质,尤其这一类数学限制题。
当答案很小的时候,我们可以通过分类讨论,用讨论法解决问题,排除掉所有简单情况之后剩下的就是那种较复杂的情况。
P9520 [JOISC 2022] 监狱
考虑分析性质,本题只有有无正解,考虑无解的情况:
两个囚犯路径有重合,且相向而行。
两个囚犯路径呈包含与被包含关系。
两个囚犯路径有重合,但处理不当,使其在中途相遇。
在分析第三条的处理,我们考虑一个合法的处理顺序是怎样的。囚犯们当然可以先安排一个囚犯走完他的路径,再同理安排另一个,这是因为每个囚犯的移动路径是独立的,要想判断最终情况是否合法,这要知道先后顺序,这与囚犯们谁先走完路径是无关的,故这种移动策略是合理的。
所以我们取思考囚犯的一定顺序,有性质:
- 如果 A 的起点在 B 的路径上,那么 A 必须比 B 先走。
- 如果 A 的终点在 B 的路径上,那么 B 必须比 A 先走
这表现了一个决定关系,可以利用拓扑排序判断关系是否成环,发现边数达到 级别用线段树优化建图即可。
总结:
分析只输出有无解的情况可以从什么时候会无解,让后分析无解的条件,通过条件导出问题。
AT_agc012_eCamel and Oases
这个就不写代码,就写题解了。考虑分析性质:
- 一个位置能够走到的位置是是一段连续的区间。
- 根据贪心,每次跳都是灌满水后再跳,最多 次。
上面两个性质,问题就变成了:在每层选一个线段,将整个区间完全覆盖。其中第一层选择的线段是钦定的(因为要对每个出发点求是否有解)由于层数是 级别的可以暴力预处理和状压 DP,状态 为 1 表示第
层已经选了一个线段。我们要 dp 出两个东西: 表示状态 下,从左到右能完全覆盖的最右边位置; 表示状态 下,从右到左能完全覆盖的最左边位置,转移通过预处理区间即可做到转移。
但是上述转移是要枚举状态和枚举线段的,复杂度会不会爆炸呢?不会。显然的,若第一层线段多于 个,那不可能有解,在这种情况下直接全部输出 Impossible 即可。
CF1658F Juju and Binary String
考虑发掘性质,对于可爱度换一个定义:
那么问题要求子串拼接起来后仍和整个串满足上面这个式子,而且要求分出来的段数极小。
考虑从 0/1 个数入手,发现选取子串 1 的个数和为,那么有 则无解。但这是必要条件。
搞笑的是,将原串首尾成环,必然存在长为 的子串满足条件。考虑若所有子串都大于/小于整串密度,显然不可能。若存在一个子串大于,一个子串小于,由于一个子串删头添尾之后 1 的个数增加量绝对值,所以中间必然经过一个子串密度等于原串密度。
前缀和判断答案为 1 即可,否则为 2。
总结:
把题目中的链性质转化为环,会有意想不到的性质。因为在环上,每个位置是等价的。但在链上每个位置是不等价的。
同时环上长度为 的子段和的和,每个点会贡献 次,所以答案是环上所有点的和乘。
CF1097G Vladislav and a Great Legend
考虑发掘性质,首先把这个 次方但是 不大,套用经典技巧斯特林反演不难转化有:
现在问题转化为求解,考虑发掘性质。
首先 是虚树的边集大小,而众所周知,唯一确定点集就可以唯一确定一颗虚树。而且虚树于 LCA 强相关,可以以 LCA 为根,其左右孩子又能划分为另一个 LCA,即另一个子问题(子问题刻画完成)。换一种角度,如果我们知道左右孩子,我们也可以通过合并左右孩子虚树得到其父亲的答案(子问题合并)。
同时回顾题目答案求解,即让我们在所有虚树的边集中选出恰好 条边的方案数。考虑这个上面虚树计数是独立的,可以合并到 DP 里面做。故设 表示 子树内选了 条边的方案数。合并的时候两颗虚树如何合并,我们知道 选 条边的方案, 选 条边的方案,那么合并相当于将 的情况相乘让后累加即可。
即转移,设 为 的辅助更新数组,有:
还有一个部分是考虑点的状态,在合并完之后我们考虑算出 以内的虚树加 以内的虚树加 的合并虚树 即可。第一三种情况好算,第二种情况讨论一下父边的是否选即可。
所以计算答案时必须要在合并时计算(要保证我们考虑的边在点集的作用下都可以生效),这样一种方案会在点集的 LCA 处统计到。
但是时间复杂度是多少,合并边界是。时间复杂度。
总结:
观察这类 的次方式子但是 不太大的时候,考虑斯特林反演。
树背包真正的复杂度是第一维大小乘上第二维大小,特别是第二维很小的情况,要时刻注意计算。
AT_agc026_d
首先看到柱状图的形式,考虑建出广义笛卡尔树,然后在上面进行 DP。
首先将原题目的红蓝色转化为黑白色这样就能看懂,然后考虑一列染色方案有哪些:
- 黑白交替;
- 全白或全黑;
第一种方案可以直接延续或者翻转后延续,而第二种方案只能进行翻转才可以,启示在状态中分类讨论。
令 表示 这一段的长度, 表示 这一段的高度。
设 表示 这一段总方案数, 表示 这一段非 01 交错方案数,而 表示 这一段 01 交错方案数。
先不考虑高度:
再考虑高度:
即为所求,时间复杂度。
总结:
对于柱状图和多边形一类的 DP 问题,我们可以通过笛卡尔树结构作为 DP 主体。
当限制特殊情况很少的时候,可以考虑分类套路怒,并将分类讨论的情况融入 DP 的设计中。
树形不仅有自下往上合并,也有自上往下递推的写法,这一类经常在笛卡尔树分治出现。
P7163 [COCI 2020/2021 #2] Svjetlo
这是困难的,但也是好的,第 299 道紫。
原命题叽里咕噜可以转化为树上路径问题。有起点和终点不固定,每经过一个点就可以置反当前状态,问最短路径使得所有状态为。
显然考虑 DP,但是我们 DP 的顺序,考虑枚举法确定我们路径的起始点,令我们枚举的点为。那么将这个枚举的点 作为有根树提起来。然后考虑如何在这个有根树上进行 DP。考虑一条路径会有如下两种情况:
一个直下,一个绕一圈在回来(南下和北上)。考虑 DP 状态中我们需要融入这个状态,设 表示 子树内都为,是否返回 点,当前最终状态是 的最短路径答案。
转移不太好直接转移,考虑合并子树答案,以下令 为转移临时存储更新后答案的数组, 运算代表异或,转移考虑枚举最终状态,以下转移按顺序进行:
以下解释转移方程。根据上面的图,我们有两种路径模式:直下和绕圈返回。贡献我们可以分摊到边的贡献,对于 的第一部分就是在绕圈进行分讨:
- 常数 代表回路一条边经过两次,固定贡献。
- :我们把 子树当成一个完整的回路,然后我们将两端连接,由于绕了一圈 一开始就是被置反过的,所以为。
- :依旧是回路,但是 这里最终状态变了,因为经过路径会使得 被取反两次,为了使得贡献能够匹配上,我们要把内部在做一次回路改奇偶的操作,这个返回使得 子树内边经过 次。
第二部分是直下:
- 常数 代表边经过一次。
- 代表 需要返回而 必须要,我们两部分用路径穿起来即可。
- :同样是穿越,但是我们也要和上面一样来通过做一次改变奇偶性的操作来使得贡献能够匹配上。
对于 的同理,这里不再细说,但是只用分讨回路的情况即可,因为因为要回到。
对于合并当子树已经保证全为 的时候可以不用合并,对答案无影响。直接做,时间复杂度。但是注意到转移只有和式,可以通过换根 DP 来进行代替枚举法的决策。具体的,我们需要维护一个 表示前缀儿子 合并后的数组和后缀 合并后的数组,转移利用 和 即可,具体见代码,时间复杂度 但有巨大常数难泵。
总结:枚举法可以帮助我们确定决策,虽然我们可以在后面优化掉,但这是一个优秀的决策确定方式。同时对于树上路径 DP 问题(不要和点分治搞混了)可以考虑枚举起始点,然后通过换根 DP 确定。
P6773 [NOI2020] 命运 - 洛谷
为什么上一题不是黑?我没有对这个题有意见这个题很好但是上面这个题是紫这也太炸杠了吧。
发现最近做 DP 题已经养成一个完整的流程了,这是极其好的。
首先考虑发掘性质,题目叽里咕噜看不懂,但是有几个性质挺好:
- 对于一个 及其配对祖先,我们只需要选择最深的 即可满足限制。
- 一个点 将其下属边置为,会影响其子树内部分点的限制,但这个限制影响当且仅当范围包含(即最深祖先仍在 上方)。这个操作一开始看见有 “存在” 我就哈气,直接就转为钦定边为。
第二个性质是第一个性质的推论,其本质就点明了子问题的设计,即限制影响的设计。
两个性质启示我们 DP 状态的设计应当包含这个限制影响范围。设 表示 子树内限制祖先深度最远到了深度为 的祖先,其他我们都保证合法的方案数。
转移考虑一个一个子树合并,利用性质 2 我们可以枚举边权设置为为 转移。
- 边权为:我们把儿子一些不合法的情况清楚,如果比 还大那就没法解决,统计为。
- 边权为,考虑合并并且讨论大小关系:
- ;
- 。
时间复杂度为,但是发现转移是一个区间形式的转移,考虑用线段树优化这一过程,第一个式子是全局乘,第二个式子是前后缀乘法,可以利用线段树合并优化这一过程。时间复杂度。
总结:
本题目的精髓在于状态设计的方面,在很多带限制的树形 DP中,我们会遇到一种现象就是子树内部能解决一部分限制,但有些限制不能在当前子树内解决,只能依赖于“更高的祖先”去兜底。本题目的限制 说明的就是这一点。
所以 DP 状态不能只描述当前子树内部已经解决的情况,还必须记录子树内尚未解决、但需要祖先去兜底的“残余需求”。
这是一个经典模型,以前没记录过只在脑海中有影响,现在把他记录一下,即树形 DP 留一部分问题给祖先考虑的特征状态设计。
同时像这种具有前后缀和转移关系的 DP,我们可以通过线段树合并进行优化,另一个题用到这个技巧的就是 P5298 [PKUWC2018] Minimax - 洛谷
Gym102798K
这玩意我是真做不出来,少一个性质都做不出来,而且关键是掐死在我不了解的地方。不过这个性质刻画真挺好的吧?
给出一个长为 的排列,现在要把这 个点按照下标顺序依次建立 BST。给定区间,问把 区间重排(顺序随意)后使得 BST 最小深度和是多少。
。
接下来,你将看到看起来比较简单性质。
考虑这玩意怎么建树,BST 我看不懂,但是我换成笛卡尔树就看懂了。换成笛卡尔树就是以下标作为堆键值,以 作为满足二叉搜索树的值。
然后,考虑如何刻画这个笛卡尔树,注意到这个笛卡尔树子树管辖区间从下标区间变成了值域区间。但是我们以值域区间来刻画的话发现没有什么深度和的性质。
我们考虑把它放到坐标系(没错这个我用了将近很长时间才想出来),坐标为,那么笛卡尔树的形态在坐标系上表现如下,以下为 的形态:
我们考虑操作,操作 重排就是任意交换 这些点的 坐标。
考虑设这些点为关键点,然后我们手摸几个交换操作不难发现一个性质:
- 关键点所形成的极大连通块进行重排操作只改变内部的结构,而且不会相互影响,其他连通块的结构都不变。原因就是因为不改变其他点和关键点之间的偏序关系。
我们考虑借助这个来进行重排过程,我们 DP 的主体就可以对连通块进行考虑了,但是深度和怎么刻画,接下来我们就要用一个我不知道的二叉树性质:
当且仅当,若为 需要额外加。
现在问题转化为最小化关键点的子树大小和,我们设连通块大小为,我们把这个连通块内接的 个子树全部都取出来,让后将里面所接的 个子树全部都取出来,然后将它们的 按照中序遍历排列成,让后次拿一个根然后把区间划分成两部分。这是区间 DP,设 表示区间 所得最小子树和:
时间复杂度。
总结:
深度和学到了可以用子树和上进行规划来转化。
二叉搜索树可以转成笛卡尔树建立,这启示我们简单结构可以从复杂结构反推。
树重排规划问题联想区间 dp,因为它的枚举断点过程其实就是树枚举根的过程。
P11364 [NOIP2024] 树上查询
人生中第 300 道洛谷上的紫!
一眼数据结构题,但是我们做题步骤也可以借鉴 DP。考虑发掘性质,首先这个 操作如何刻画呢,考虑所有操作都是 LCA,多次涉及 LCA 考虑往虚树考虑。
然后发现这玩意其实就是。证明用虚树逐渐加点就可以证明。至此,我们可以解决 B 性质,B 性质的本质就是在问上面,可以 预处理 LCA 加线段树求得,这样我们就有了 12 分可以做啦。
接着我们考虑有了这个段如何做?考虑发掘继续发掘性质:
- 题目所有询问的区间都是编号连续的区间,且询问可以离线。
- 固定右端点,延申左端点 单调不降。
首先定个目标时间复杂度为。
然后根据题意模拟将询问离线下来,我们可以暴力根据 预处理询问,然后暴力处理,时间复杂度,无法通过。考虑优化,发现优化不动,因为无论怎么着我们都需要把询问都提前暴力预处理出来。
正难则反,考虑反着做,但是对什么反着做?考虑我们是根据 预处理段,然后询问答案。但是我们已经有的信息就是 LCA*,能不能枚举答案,然后询问有没有长 的段呢?
这样做或许可行,先简化问题,将上面区间的性质拆为,但是答案很难搞,我们把这个答案拆分贡献,将贡献拆到每个点上。即这个点贡献 LCA*。
我们有长为 的序列,值为,另一个 的 01 序列初始全为 0。 考虑在答案值域上从大往小扫,那么从,就会出现几个点被设为 1,而询问要求问的是有没有 长度的极长连续段。可以通过线段树维护最大子段和或并查集来做到。
接着考虑有了区间限制,考虑这个区间限制如何合法,,不难分讨四种情况:
- ;
- ;
- ;
- 。
最后一种显然合法,第一个可以拍入到其他方案,而第二个第三个需要对 单独计算,是一个二维偏序,可以用扫描线做,但是直接做是三维偏序,很难维护,考虑进一步发掘性质。
我们考虑从大到小扫描,将 的询问拆成左端点询问到,右端点询问到。
时间复杂度。
总结:
本题目作为 NOIP T4 完全合理。部分分不知道链有什么性质。
正难则反什么时候会用到,你需要考虑正着做是没有前途(即无论如何都无法简化问题),那么可以考虑正难则反。
从简单情况入手,一步一步思考。同时数据结构能离线则先考虑离线,离线能够将算法卡死在一定范围内帮助思考。
在题目多次涉及 LCA 的时候往虚树思考,利用虚树来去刻画题目的限制。
AT_abc216_h
好题,以后看到不相交路径可以直接开始哈气了。
首先假概率,实际上。
那么现在问题转化为求解上面的东西,注意到这玩意有一套成熟的东西叫做 LGV 引理。但是我们知道的是 LGV 引理是有起点和终点的,但是这里只有起点没有终点。显然不能直接做,那么回归老本行,考虑发掘性质:
- 。
- LGV 引理的本质就是行列式求路径计数问题,是进一步的引理推论。
首先第一个性质至关重要,由于没有不相交路径,我们可以考虑枚举终点,那么从起点走到终点的方案数简简单单就能够算出来就是。第二个性质表明路径计数的本质逆序对计数,可以转化为以下式子:
其中 还是行列式那个奇偶性的容斥系数。显然可以用行列式计算,但是枚举 的成本过大。
注意到 且值域极小,考虑状压 DP。我们主体在 的值域上进行规划。设 表示目前处理到坐标,目前已经状态为 的起点确定了终点的合法方案数。转移就是枚举是否有一个起点选择位置 作为终点(显然合法方案不会有两个起点走到一个位置作为终点)。
枚举哪个起点选择 作为终点,有转移:
答案即为,其中 为值域,时间复杂度。
总结:
路径不相交问题首选逆序对容斥,然后分为两种情况:如果终点确定那么可以套用 LGV 引理;如果数据范围小那么可以 dp 计算容斥系数。
状压 DP 当然也可以用于确定序列,这个技巧同样在确定排列插入法的时候用过,时间复杂度会贡献。
AT_arc121_f
好题,因为这个题我直接在性质就翻车了。
对于这种构造操作顺序的题和合并问题可以从叶子开始考虑。
分类讨论叶子和连边情况:
- 叶子为 0 且边为
AND:操作这个点会让父亲为 0,优先操作一定最优。 - 叶子为 0 且边为
OR:可以省略无影响。 - 叶子为 1 且边为
AND:可以省略无影响。 - 叶子为 1 且边为
OR:叶子以外的部分任意操作,最后都能合法。
除了第一种情况剩下的我们都可以无脑操作。根据上面的结论我们可以暴力讨论写50行转移方程。但是官方给出更方便的做法,设 表示子树内不存在 1 or 的情况, 表示 中合法情况个数。转移:
- 考虑边是
and或or,我们把1 or的情况除掉:。 - 考虑是
1 and或0 or:。
答案考虑容斥原理,就是。
总结:对于这种构造操作顺序的题和合并问题可以从叶子开始考虑。因为叶子是树中最灵活的部分,就像质数在数论构造中的作用。可用于保证某个相关数值“能够调整至任意一个 内的值”。从叶子自底向上考虑是一个很好的思路。这个是我第一次见在其他地方运用这个技巧。
P8392 [BalticOI 2022] Uplifting Excursion (Day1)
背包好题?
考虑发掘性质,注意到本题是多重背包,但是炸杠的是背包容量过大。考虑发掘性质,注意到背包物品容量极小,但是数量极大。考虑多重背包的做法有一个叫二进制拆分的做法。看一下能不能行。
首先将所有物品都进行二进制拆分,形式会如同。我们考虑将这个剩余大小完整拆分到二进制,然后将物品分配到对应的二进制位。
然后从低位到高位跑背包,设 表示当前考虑到数位,容量为 的最大选取个数。但是注意到这样容量这一维度显然会炸掉。但是我们发现我们数位就是在容量的二进制数位上进行 DP,考虑利用 进行优化,重设状态,设 表示考虑到二进制瞎数位,容量为 的最大选取个数。
但是如果直接做的话还是不太行,因为我们贡献是累加到 的,继续优化,考虑一个动态的状态设计(Desant 后遗症),我们到下一个数位的时候可以将上一个的数位贡献去掉,那么这样第二维的状态数量就在 级别。时间复杂度为。
总结:
总容量大,但是物品重量很小的背包,可以按二进制位考虑压缩有效状态数。这种动态的状态设计可以优化掉一维度很大的方法,是一个不太常见的优化方法,类似的题目在 P5972 [PA 2019] Desant - 洛谷 出现。
CF1239E Turtle
一巴掌给我扇飞了,好题但是我是 zz。
首先考虑给定矩阵,如何刻画乌龟的路径,有性质:乌龟走的一定是第一行从开头的一段的连续路径,然后下去走到头。故设 表示第一行的前缀和, 表示第二行的后缀和。那么答案就是。
考虑重排操作有没有什么性质,有一个贪心的想法,我们让第一行从小到大排序,第二行从大到小排序,这样列列操作一定是最优的,证明考虑从逆序对入手进行反证法即可。然后问题转化为行行之间刻画,可以考虑利用 DP 进行计算,但是代价计算是。我们没法进行转移啊!
考虑简化代价,我们考虑排序的会对乌龟的决策带来什么决策,关键性质:乌龟要么在开头就往下走然后走完第二行,要么走完第一行然后往下走走到终点。
那么代价可以简化成:。前面是固定的,后面是不固定的。直接飞上去 DP 进行决策:设 表示考虑到第 个数,第一行一共选了 个数,选出数的总和 是否可能。最后让总和尽可能对半分即可。
注意到这个是可行化 DP,但是值域和 极小,可以用 bitset 优化,时间复杂度。
总结:
本题目创飞我一点就在于简化代价计算,比如取最大值的代价可以考虑会在那些地方取得(相当于拆分贡献思想),如果代价复杂 dp 是转移不动的。
同时本题目也体现了一个背包组合的约束现象,很多时候背包会存在(隐藏的)拓扑关系,这时候的结论可能是选了小价值物品就必须选大价值物品。
CF1481F AB Tree
很可惜我不是来这里学二进制分组加 bitset 优化多重背包。我是来这里学完全背包优化可行性多重背包的。
注意到答案很奇怪,写个暴力(自从那个构造之后就有写暴力发现性质)发现答案上界在最大深度和最大深度加 之间徘徊。
考虑分析最优解构造,注意到答案和深度有关。考虑按层构造,每一层我们尽量填入相同的字符,设出现次数较大的字符为 ,因为要降低对儿子的影响,所以把非叶节点填入颜色 ,设 为未填写的字符,因为非叶节点的出现次数,而,所以一定能填满,然后把 填入这一层的叶节点,剩下的就只有另一种颜色的,填入到其它点中,不难发现只有当前层会多一种不同的字符。
那么现在问题转化为能不能每一层都能填写相同字符,若可行输出用 DP 求解答案并输出方案,否则贪心按照上述方法构造即可。
不难发现这个 DP 可以当作背包 DP,把每一层的节点数量当作物品,那么这就是一个多重背包可行性问题。直接做是 的,但是发现物品种类数最多 级别的(。可以通过 bitset 加二进制分组优化到,输出方案可以加个回溯也是 ok 的。但是问题在于我不是来这里学这个的。我们换个思路,因为多重背包求解的是存在性问题,可以转化为类似完全背包的模型。
具体的我们通过背包维护剩余数量,设 表示用前 种物品凑出 总和。若 则不可能凑出。若 表示第 种物品还剩下 种没用。
转移考虑分类讨论,令当前物品重量为,数量为:
- 不使用第 种物品,当且仅当。则。
- 已经用过第 种且 可行。则。
实现中转移需要 从小往大遍历。这种用完全背包把数量限制转化为记录剩余数目的技巧有点常见。
总结:
一类不关乎价值只关乎重量的可行化多重背包可以用完全背包把数量限制转化为记录剩余数目。将空间简化。
P3780 [SDOI2017] 苹果树
这是什么背包?
咨询 CatGPT 有一个我没理解的题意:选取了一条节点,那么从这个节点到祖先都要取。这个性质很好,问题相当于选择从根到某个点的路径,免费选一个苹果,再做树上依赖性背包。这个点肯定是叶子,因为多选免费苹果一定更优。
然后考虑 有什么用,简单变形为。注意到 就是最长深度。通过枚举法我们钦定一条到叶子的链作为最长深度(显然在上面)。然后剩下的就是简单的树上依赖性背包,直接做的话时间复杂度,无法通过。考虑优化这一过程。
首先枚举法不能丢,我们发现对每个节点都重新求答案还是太超标了。能不能利用一些共性答案,我们发现如果以这个链把子树劈开,会分成左右两边,左边和右边是独立的与链无关,可以通过树上依赖背包算出来然后合并答案到一起。具体的,类似序列上的前后缀背包合并,我们求出正 dfn 序的背包和逆 dfn 序的背包,然后把它们合并起来就可以得到答案。
求解正序背包时,我们把必须选取的点(指选某个点导致其链上的点必须选取)和随意选取的点分开。进入一个点的时候加入随意选取的点,递归时把当前背包复制给儿子,然后从儿子回溯时加入当前点。
向背包中加入随意选区的点可以用单调队列优化,而逆序把建边从大到小编号建边即可。
答案合并就是 当前链长度,时间复杂度。
总结:
枚举法真的很好用!可以帮助我们确定决策,最好用的一集!
这种 DFS 序的多重背包其实正式名称就叫树上依赖性背包。树上依赖性背包形如在树上选出若干个物品做背包问题,满足这些物品连通。由于 01 背包,多重背包和完全背包均可以在 的时间内加入一个物品, 的时间内合并两个背包,所以不妨设背包类型为多重背包。是前后缀背包思想的运用。
CF917D Stranger Trees
等会,题面这个图还有题目背景,莫非是?
咳咳,回到正题,首先看到 “恰好” 直接哈气。用二项式反演反演成至少,有:。其中 为答案, 为至少 条边相同的方案数。
然后考虑 怎么算,发现这玩意我们把钦定的 条边断开,会形成 个连通块,而这些连通块都是独立树计数的。根据 Prufer 定理有任意连边方案数:
为连通块个数,其中 还是连通块大小。
然后考虑如何快速计算,发现如果直接做因为边不确定状压直接爆炸。数据范围,考虑发掘性质。
我们考虑把 的组合意义拆分,前式子可以随便计算,而后面却要求我们快速不用状压计算。考虑 DP,设 表示 子树内,分成了 个连通块,当前 所在连通块大小为 的方案数。时间复杂度 可以 转移但是我认为是 就很难泵。
但是我们显然有更好的做法,考虑我们只是在计算,考虑复杂度瓶颈就是在于这个 这一维度让我们的优化没有前途。考虑切换组合意义,发现 的本质就是给每个连通块内部任意定根的方案数,把根是否确定放进状态中即可。
那么这很好考虑设 表示 子树内,分成了 个连通块, 所在连通块是否定根的方案数,转移用背包对子树合并即可,时间复杂度。
总结:
- 当我们组合意义出现嵌套的时候,方法就是给我们的价值函数确定一个组合意义。常用的技巧是拆分法,把复杂的价值函数拆成几个可独立处理的部分,然后分别计算再合并。这个时候 dp 就需要同时完成确定局面和组合计数的功能。
- 当我们在对具有组合意义的价值函数进行 DP 的,如果我们发现优化不动(确定没有前途)那么我们可以考虑切换组合意义,来达到优化的效果。
8.22 模拟赛 T3
2025 牛客多校 Ghost in the Parentheses
全场唯两个可做题。首先这个概率又是假的,直接拆成。
首先考虑什么时候括号序列可以唯一确定,由 GF 惨痛经历我们将 ( 抽象为加,将 ) 抽象为减。
我们考虑,假如你是 Bob,你收到一个字符序列如何确定唯一?根据上面的法则,大胆猜想有一个结论:考虑去掉所有问号,我们对原序列按照上面做前缀和,记总和为。当,我们就把问号去掉一个,同时。若 但是还有问号,那么显然不唯一,否则唯一。
严谨的:定义从左到右扫描,设在位置 之前(含已固定的 ?)的平衡必须取某个确定值(否则不能满足末尾为 0 或中间某个前缀非负)。若在某个时刻偏差为,则为了保证后文能回到 0,接下来至少要出现 次取 的位(这些要么在已知字符里,要么必须由 ? 来承担)。若这些 必须由特定位置的 ? 来提供(因为已知字符的位置和数量固定),那么这些 ? 的取法就被唯一决定;重复此论证直至结束,所有 ? 都被唯一确定。因此当贪心能把 一步步消到 0 恰好用尽所有 ? 时,没有任何 ? 是“可自由选择”的,从而合法补全唯一。
然后我们考虑这个结论怎么用?这还只是我们知道序列,但是现在不知道序列,我们思考什么时候我们能唯一确定 ?。
令 表示前缀左括号个数和于前缀右括号个数和。我们发现当一个某个位置前缀和为 的时候,那么一定是形如 合法序列+ ( 的形式。那么我们可以发现,如果我们把里面的 ( 随意改变为 ? 的话,根据上面的结论,不会影响答案,因为这些 ( 会被唯一确定,组合数。同理于右括号,每个右边的 ) 仍然可以自由选择是否变成 ?,故一个前缀和为 的位置贡献是。
通过加法原理和起来答案即可,但是会发现算重,我们算一个位置的贡献要减去下一个位置的贡献即可,时间复杂度。
总结:不确定的元素可以思考其中的确定性作为突破口统计答案。
CF1615G Maximum Adjacent Pairs
本题将不实现,原因涉及算法等级超标,但是这种建模思想和思路过程还是需要讲一下的。
考虑分析性质,首先不难观察到如下的性质:
- 值域 较小,对于 的限制条件计数只会算一次。
- 对于单个 的情况,可以考虑贪心的去匹配,即考虑左右两边挨的数是否已经匹配过了即可。对于多个 的情况,其左右两边可以根据前面所说的贪心匹配,而中间的段会单独贡献答案,可能需要特殊计算。
- 确定值的过程可以看作类似于二分图匹配的问题。
以后遇到这种问题,我们要出动三小只:DP,贪心,图论等其他模型建立。
考虑 DP,根据上面的性质显然有一个 DP 的想法就是设 表示到了第 个 数,当前相邻限制出现集合为。时间复杂度直接超标,考虑优化,发现这个限制是全局的,如果我们通过 DP 在构造过程中不去记录那么会不满足。容易发现 DP 是没有前途的,遂放弃。
考虑贪心,前面的性质我们已经提到过单个 的情况可以任意贪心,然而多个 是不太好去搞这种决策的,因为这个是具有后效性不太好搞,但是注意到我们是在注意确定值,而且要求恰好计数 1 次,这不就是图的匹配问题吗。
考虑图论模型,我们从这个题开始将开始大范围的凸轮联系,我们要和 DP 一样标准化做题流程。以这个题为例:
图论模型的建立
首先我们要考虑对什么对象建立模型,即我们要选取建模主体,然后考虑用图论的意义来去表示原问题。
一般情况,我们会以题目的一个限制为基础建立模型,这一步不要被思维定势所局限,大胆去想,小心求证!
注意到我们是将 的值一一确定,且根据前面的相邻限制,一个值只会被计入一次,这是一个类似于二分图匹配的问题。
图结构的分析与建立
我们思考原问题中各元素在图上的含义,一个值只贡献一次告诉我们把值建成点会好一些,同时我们把 0 也建成点,
0 的填法产生贡献相当于和对应的值匹配,我们建立边就可以决策这个过程。
更具体地可以考虑原序列上连续的一段 0,根据贪心原理只有连续段边上的 0 才会和值匹配,其他的 0 都另寻它路了,简单讨论一下:
- 如果连续段的长度为偶数,那么我们建立两个代表 0 的点 x,y,首先将 x,y 连一条边代表他们可以自己匹配,然后我们将 x 连向左边的值,y 连向右边的值。
- 如果连续段的长度为奇数,那么我们建立一个代表 0 的点 x,把它和左边的值和右边的值都连边。
转化问题加寻找结论
如上建边,我们可以通过跑最大匹配来去解决问题,这个时候由于图显然这样建边会存在环,我们可以通过跑一般图最大匹配来去解决,然后就做完了,至于那些神秘的优化那都是后来的事情了。
总结:
这种题目属于一种难以处理的全局限制,这种全局性限制之所以难以处理就是我们无法拆分为独立的限制来去解决,以后遇到这种难以处理的全局性限制我们可以以图论的角度来去解决问题、
CF1368G Shifting Dominoes
性质最多的一集,这是解题报告,所以会比较长且出现一些导向型但非正解的做法。
显然考虑计数,但是我们先分析性质再考虑用什么做法维护,在看题过程中不难发现如下性质:
- 所有骨牌最多左右上下移动一格。且一种方案有且只有两个空位。
- 对于移动所产生的效果的移动是连续的,以空位不断向外进行拓展。
- 看见方格图就哈气进行黑白染色,那么题目中删掉块所产生两个相邻的空格是黑白不同色的。
- 由性质 1 导出计数过程,方案是对局面的空格位置进行计数。
这些是一些基本的结论,通过性质 4 我们发现我们要将我们的计数主体放在空格上而不是方块上。
然后我们考虑一次骨牌移动到空位会产生什么影响,有图,这张图黑白染色改为了蓝红染色以作鲜明区分:
竖过来也是一样的,这种我们不好用 DP 来去解决这种空格移动,但是我们可以通过图论模型来表示这个操作!具体的就是根据上面类似的进行建边转移即可。
同时我们还能从这个图导出一些性质:
- 根据上面图和建边方式,不难发现一次移动两格,而我们图是黑白染色。也就是说一个空格移动所到达的点一定和这个空格同色。进一步的,也就是说黑色格子和白色格子是互相独立的。
- 所有点入度最多为 1。
性质 5 和 6 是非常好的性质,我们可以通过性质 5 导出独立性的结论,这样我们只需要对黑色格子和白色格子单独做一遍这个图论。而性质 6 通过和前面性质 2 结合起来能够说明本图至少是一个基环外向树。但是进一步的(显然我没想到这一点)可以发现本图不存在换,因为反证法,加入存在一个环,那么通过上面操作可以移动一圈将空格子回到原点,但是原点已经被一个骨牌覆盖了。
那么更好啦,这个图就是一个外向树森林,那么一个空格子所能转移到的都是这个森林某个树的一个子树,根据前面的性质也能导出来两个空格的移动是独立的。这是一个二维矩形问题,各个维度代表独立的格子,且到达的子树可以表示为一个 DFN 区间。那么我们可以通过扫描线求矩形面积并来解决这个问题,时间复杂度。
总结:
以后遇到这种矩形中类似推箱子的问题,可以把箱子的移动转化成空格的移动,建立关于空格移动路径的图。同时本题目我们通过性质 5 导出独立性的结论,将多个对象的问题可以找独立性来转化成单个对象的问题。
以后看见方格图就可以哈气染色,哈气是好习惯。
CF1458D Flip and Reverse
不是上一个题那么多性质,我做这就很高兴。现在一个性质都没有?
这种数量相等可以借鉴检验括号序列的思路,我们将,那么做一个前缀和,那么操作的第一个条件数量相等就可以表示为前缀和,那么一个合法子串 能够被表示的条件就是。然后就找不到性质了。
然而实际上我们可以通过前缀和的变化来看(差分),这种复杂的区间修改操作我们可以通过差分的思想来去解决。
我们考虑 的变化,考虑按照原字符串建立一张图。对于每一个 值建立一个点。例如说现在的 值为 , 遇到了一个 1, 然后我们从 到 连一条无向边。
选择一个 1 和 0 数量相等的字符串,前后的 值一定相等。于是这就形成了一个环。
考虑将这个字符串取反,其实相当于从这个点绕着这个环走一圈。
然后我们要求的是这张图的最小字典序的欧拉路径。
可以考虑贪心,能向小的数走就往小数的走。
怎么判定数 t 能不能往小数 t−1 走?首先一定要有 t 到 t−1 的这条边,如果 t 有到 t+1 的边那么 t 到 t−1 的边数至少为 2 (肯定要返回 t)。时间复杂度。
本题所考察的知识点最高难度等级为 6 级,并不算高,为欧拉路径(6),贪心法(3),前缀和(3),string类与相关函数(2),数组与数组下标(1),cin语法scanf语句cout语句(2),for语句(2),难度不超过提高组所规范的难度,考察了选手图论建模的能力,实现标程极为简单。但预期绝大多数选手无法获得有效分数。
总结:
这种区间修改类的问题我们可以通过差分的思想来进行转化,区间元素和的判定问题可以把前缀和建成点,原图中的元素建成连接前缀和的边
CF1361E James and the Chase
DFS 树经典应用。
首先考虑如何判断一个点是合法的,考虑建出 DFS 树,由于这是有向 DFS 树,那么会出现三种边:树边,横叉边,返祖边。不难发现只有横叉边只有一个不满足条件,所以只要保证 DFS 树里面没有横叉边即可。可以 判断啦。
然后你发现复杂度是线性 的直接爆炸,因为一次判断复杂度是。考虑进一步发掘性质,我们无法枚举所有的点,也就是说我们只能枚举部分点,然后从这个部分点推出所有点的答案。
我们根据上面判断法则进一步推广,不妨设我们枚举的一个合法点为(显然可以 判断),那么先建立出 DFS 树,然后我们考虑一个结点 如何判断合法?
直接找充要条件显然是炸裂的,先找必要条件,首先由于是有向 DFS 树,一个点合法是能够到达所有点为前提条件的,那么它想要走出子树到达其他点显然只能靠返祖边,横叉边不行因为一开始我们枚举 判断子树内没有横叉边了。
进一步限制这个从子树内走出子树外的返祖边有且仅有一条,否则 到祖先就有两种方案一定不合法。
现在考虑构造充分性,上述条件能走出子树有且仅能到达祖先点,但缺乏的条件就是到了祖先出了子树也可能也到不了其他点,或有多条路径。那么我们构造充分性,即返祖边连向的点 必须是好点,这样构造就能够保证简单路径唯一。用 set 启发式合并求出子树返祖边即可,时间复杂度。
现在我们可以遍历一次求出所有答案啦,但是还有问题在于如果我们暴力枚举每一个点然后进行判断是否合法,求解是 的,无法承受,而且我们无法进一步优化。考虑到题目中 个合法点的限制,我们从这个限制入手,导出条件也就是说一个点有 的概率为关键点, 的概率不是关键点,那么我们考虑随机化,随机点然后判断是否合法。那么设进行了 次随机化,那么错误概率为,当 取 100 左右时错误概率约为,可以忽略不计。
总结:图论问题再判断合法性一定要主动放在 DFS 树上进行考虑。这个题有两个难点,第一个就是 DFS 树的综合利用以及判断,第二个就是这个 20% 的限制,这个 20% 是一个关键的阈值,如果达到了 20% 就能做某事,如果达不到 20% 就可能做不成某事(不是一定做不成),那么思考这件事是什么即可。
CF901D Weighting a Tree
先从简单情况入手,首先当 的情况,也就说原图是一个 个点的树我们如何构造。这种树的构造方法一种常见的切入角度就是剖叶子。那么就有构造方法,即从叶子开始自底向上构造,要让叶子合法边的权值只有一种可能,所以最后我们能让除了根的所有点都一定合法。这样构造能够根据根是否合法直接给出解,因为显然不存在另外的边使得让不合法根能够获得点权合法。
然后我们加大难度,当 的时候如何构造?首先 原图就是一个基环树。注意到边权可以为,考虑断环为链,这里就是我们选环上的一点作为根,然后将这个 在环上所连接的一条边边权设置为,然后就可以按照上面的树方法做了。如果 点权为,显然万事大吉。但是如果 不为,那就不好说了,因为我们和上面树条件不同的地方在于我们这里有了一条可能让 合法的边。
现在的情况是我们有了一个除了 以外不合法的方案,现在我们尝试简化问题。首先这是一个基环树,我们可以把环上挂的子树都给删掉,只保留环,因为环上的子树答案显然是上述 的子问题,答案已经被唯一确定,所以现在我们只需要考虑环上的问题即可。我们可以通过调整法通过调整环上我们一开始赋值为 的边来保证合法。考虑到到现在我们都没有利用题目中的奇偶性,我们考虑利用这个奇偶性来作为我们的条件入手点。
先考虑答案如何构造,首先找必要条件,由样例 与 能够导出一个结论,环根的点权必须是偶数,否则无解,证明考虑分类讨论:
- 如果 的点权是奇数,那就意味着它在环上无法平分,无论怎样调整 的位置,都会导致一边奇一边偶,矛盾。
- 如果 的点权是偶数,它就能被分成两份分别放在两条路径里,这样才可能调整出合法情况。
接下来考虑充分性证明,我们考虑从这个赋值为 的边构成环的来考虑,考虑到偶环是没有用的,因为它无法使得修改的带你全集中在你要修改的点上,并且偶数长度导致在调整边权时符号在回到起点时相反,两个连接到根的边得到的调整是相反数,相加为,总结下来就是调整偶环无法改变答案。
我们再考虑奇环,如果非树边设置的权值为,那么调整非树边 会使得环根权值变化 或,证明用在环上的距离证明即可。根据必要条件环根为偶数,所以一旦出现奇环必定有解,故如上构造即可,时间复杂度。
当 时,找出原图的一棵 dfs 树,然后把非树边的边权赋值成 0,按照 的方法去做,我们找出奇环,把奇环的环根当成树根建树,然后按照上述条件调整即可,时间复杂度还是,当然你也可以任意挑出一个生成树,但是还是 DFS 树没有横叉边的爽。
总结:很多变元的构造题中,可以只考虑少部分的变元就能给出构造方案。直观上好像每个地方都能改,但实际上很多地方是“被迫的”,一旦你确定了某些关键部分,其余部分就自动唯一确定了。
CF1019C Sergey’s problem
调整法真好用 (•ω•)
先从简单情况入手,我们先从链的情况入手,可以按这样的方法构造出点集 :选取一个点 ,然后删除所有满足存在有向边 的点 ,持续这个过程直到不能操作。这个操作可以进一步拓展到树,最终能拓展到 DAG。对于树的拓展是显然的,而 DAG 考虑做一次拓扑排序,按拓扑序贪心选一次即可。
考虑进一步拓展到有环的情况,但是发现很难拓展因为会出现连边的情况。考虑分析点集的性质,它满足所有点可以通过选取点一步之内走到,但是根据构造的特点,可能后选取的点向先选取的点连了边。但是考虑到两步之内走到的限制更为宽松,我们可以在此基础上调整。
注意到,我们选出点所能构成导出子图时 DAG,考虑用拓扑排序调整,对于我们选取的点,如果存在 被选取并且,那么 就不用,否则必须保留。这样就不会产生冲突,且所有点都可以在两部稚嫩走到,时间复杂度。
总结:
调整法是一个很重要的构造方法,如果存在两个需要我们构造满足的变量,我们可以先让初状态先满足一个条件,然后再调整。此时初状态的选取依然很重要。
从简单结构拓展到一般性结构是一个重要的思考方法,DAG 的思考具有一般图所没有许多性质。
AT_joisc2016_i 電報
一会喂我好吃的,一会喂我史,为什么呢?
考虑出度全为 如何利用这个关键性质,既然要保证原图强连通且出度都为,那么经过操作后图一定是一个大环,即所有点入度为。同时容易证明原图除去一开始的合法情况一定是个基环树森林。
显然 DP 不好处理,考虑贪心,有一个显然的贪心就是将每个点保留权值最大的入边,其他入边贪心的删除即可。然而这样操作后会形成若干个环,我们需要将这些环接成一个大环,考虑这个具有什么贪心性质,发现环上必定会断开至少一条环边然后和其他环接起来。所以预处理非环边的最大权值,然后贪心地看替换环上哪个点最好即可。具体的,设 为所有连向 边中代价最大的, 表示不属于 所在环中连向 边中代价最大的。那么我们贪心的选取 最大的即可,时间复杂度。
总结:本题中度数和连通性是可以互相联系,但是不同的地方在于度数是单点的限制,而连通性是整体的限制,我们考虑单点限制是比整体限制一般情况下是比较简单的,再考虑例外来修正我们的限制转化即可。
JOISC 2015 Day2」Keys
我去这不省选集训 Day1 T1 吗,不行这一次我一定要做出来。
考虑分析性质,首先注意到每一个时间点有且仅有一名社员进行出入操作,启示对时间点之间进行分类讨论贡献与开门情况,有分类讨论,以下时间点均为 之间的分讨:
- 出 出:显然让 拿钥匙可以贡献。
- 出 入:需要都拿钥匙。
- 入 出:随便贡献。
- 入 入:后者需要拿钥匙。
- 否则,门都会保持打开的状态,所以有没有钥匙都一定能合法。
考虑计算贡献,贡献 3 直接记录到答案中,贡献 2,4 记录在需要钥匙的那个人上,也就是这个人有钥匙就能产生贡献。贡献 1 记录在两个人之间的边上,表示两个人都有钥匙就能产生贡献。
那么问题转化为图上选点最大化贡献的问题,但是这个图有特殊限制,考虑每个点最多连出去两条边并且不会有环,所以这张图就是若干条链。我们把这条链的端点串起来,这样就变成了序列问题,就可以直接 dp 了,设 表示前 个点,放了 个 key,当前第 个人有还是没有钥匙,时间复杂度。
我很好奇能否直接进行 DP?但是显然是不行的,因为上面所说了链是多条的,如果瞎进行 DP 就会出现跨链的问题。当然我们也可以对每一条链单独做,然后背包合并。但是显然做法更麻烦,但是这个做法是在你一开始没想到链是森林状直接转移出错后会导出一个最直接的做法。
总结:
贡献法也能运用到规划问题中去,还是从小处入手,考虑贡献产生的条件即可,是无条件贡献?是点限制贡献?是边限制贡献?将贡献问题用图论进行刻画也是一个常用的技巧,将总贡献拆分到点上和边上。
CF1307F Cow and Vacation
这是黑吗?
分析性质,发现路径一定形如:,这种形式,其中 表示关键点(休息点)。考虑如果直接暴力去 BFS 的话显然是不行的,考虑到我们只需要判断可不可以达到即可,而路径是从 到一个关键点,然后从关键点到关键点,然后从关键点到终点。
自然引出一个想法,即我们先考虑关键点是否能到达关键点,这一点我们可以对每一个关键点维护并查集,然后通过暴力 BFS 这个题目给出的半径来维护关键点之间的连通性,设半径长度为,我们要向外拓展 的长度拓展。
同时,上面的做法也可以合并范围内的点能否到达这个关键点也是可以的。注意到上述拓展是最多 遍历的。
然后我们就可以判断,首先若 那么就不用走关键点。否则设 和 表示 和 在路径上前进 的点,若 和 联通,则可以到达,否则不行。
直接做时间复杂度,实现上因为 有可能是奇数,这个时候只需要双倍开点技巧让 变为偶数即可。
总结:可达性转连通性是一个关键技巧。
CF1534F2 Falling Sand (Hard Version)
Easy Version
分析性质,发现这个沙子掉落关系具有传递性和连锁反应,考虑用图论建模表示这种情况。
考虑用单向边表示这种扰动关系,即即若 A 能扰动 B,不代表 B 能扰动 A。考虑到建完边后一定会形成若干个强连通分量,显然随便强连通分量内的任意一个沙子都是会被掉落的,考虑缩点,得到的就是一个 DAG,而 Easy Version 由于数据保证有解而且要求沙子全部掉落,那么我们可以直接选取出度为 0 的点即可。
然而上述直接暴力建边是 的,无法通过,考虑优化建边,我们考虑沙子 下落会影响那些沙子,显然上下是具有传递性的,现在我们考虑左右,我们发现可以只需要连接 左侧第一个在它下面的点和右侧第一个在它下面的点,然后根据前面我们上下保留的边可以传递,所以这样优化之后就很好了边数为 级别的,总结一下:
- 如果这个点上方一格有点,那么连边。
- 如果这个点下方有点,那么连边。
- 找到左侧第一个在它下面的点连边。
- 找到右侧第一个在它下面的点连边。
然后按照上述做法做即可。
Hard Version
我们考虑 Hard 在哪里了,即我们不再要求所有沙子全部下落,因为同一列高的下落,矮的一定下落。那么有一个贪心的想法就是我们让每一列从下往上第 个下落即可,我们让这些点为关键点。但是原题目中的限制是具有传递性的,所以现在问题转化成选取一些点,从这些点出发能覆盖到这些沙子对应的点。
现在回到主体,显然我们的 Easy Version 建图是可以继承过来思考的,但是我们发现直接做是没法做的,因为我们根本不知道你选取的点是以如何形式进行覆盖的。仔细思考也思考不动,怎么办?
当感觉一个问题不可做时,可以检查一下自己转化问题的时候是不是漏了什么性质。——gyh20
考虑进一步发掘性质,只能从图发掘性质了,我们发现这个图建边每条跨列边都指向比当前高度更低的格子,且每到一个点,必定是向左向右只跳一列的,不可能出现左列关键点和右列关键点被覆盖,中间列关键点没被覆盖。
大胆猜想,一个点所能到达并覆盖的关键点是一个连续区间。证明考虑反证法,假如说不是连续区间,那么必定存在三个从左至右的点,使得 能到达 但是到达不了,那么根据上面建图每条跨列边都指向比当前高度更低的格子,那么可以得到 高度比 小,而中间必定会经过 这一列一个点,因为不能解决 的限制,所以 关键点肯定高于,而根据前面高度推论显然 能够到达。
那么问题转化为了选取若干个区间的并集是全集,可以按照区间左端点或右端点排序即可,这个问题就是去年 CSPS T2,时间复杂度。
总结:这题真有点牛吧,如果不同的限制具有拓扑关系,根据题目特性可能可以忽略一些限制,这种拓扑覆盖问题可以考虑在原序列上的区间覆盖性质。
当感觉一个问题不可做时,可以检查一下自己转化问题的时候是不是漏了什么性质。
CF1270H Number of Components
考虑分析性质,但是发现分析不出来性质,我们无法从连边的入手。我们考虑连通块的性质,发现连通块有一个关键性质:一个连通块代表的是一个序列的连续区间。证明考虑反证法即可简单证明。
那么原命题就被分成了若干个块区间,如果我们暴力维护块合并和分裂是 级别的,肯定这也不是颜色段均摊,无法优化,考虑进一步分析性质:
- 连通块之间互相独立,互不影响。
- 值域,且序列上所有数保证在值域上唯一表示。
对第一个性质进一步推广,即我们考虑一个块独立的条件,即什么时候会取到一个块的新左右端点(或分界点),设分界点为,那么也就是说对于, 有。由于这个序列是被分界点分解成若干个块,考虑到只需要对这些分界点计数即可刻画连通块个数。
第二个性质启示我们值域较小且数被唯一标识,有很大的指示性提示我们要在值域上规划,考虑一个分界点的条件,这是偏序问题吗?不是,我们考虑枚举一个阈值,对于序列中 的设置为, 的设置为,那么原命题转化为求生成 序列使得形如 的阈值个数。
考虑对于每个 我们维护生成序列 相邻数对的个数,如果数对个数为 就是合法的答案。可以用线段树维护,对于原序列上两个位置,其中 的数对个数就会增加。
为了方便我们设置,,因为 个数至少为,所以我们维护最小值和最小值的数量即可,时间复杂度。
总结:
这题是真的神,这种序列大小关系的处理我是第一次见,序列大小关系的处理可以转 01 序列,大于某个权值设为 1,否则设为 0,然后研究 01 序列的性质。
序列图论题的结论思考方向:图论某个量和原序列区间的联系。
维护某一个特定值的数量,思考他是否一定是最值,是的话转成维护最值和最值的数量。
[AGC008E] Next or Nextnext
这个我是真难泵的,题解看 题解 AT2267 【Next or Nextnext】 - 洛谷专栏 的吧我还是太菜了 www。
总结:这种双图刻画限制我还是第一次见,双图策略可以帮助你充分考虑已知信息和所求,通过思考两个图之间的关系来发现问题性质。
LOJ521 绯色 IOI 抵达
每做一道难题就要去 zxy 上找点清淡的吃。
又是构造题,树的构造先哈气考虑剖叶子。那么不难发现真是个天才的想法,因为叶子是唯一确定选择父亲的。
然后进一步发掘,由于题目每一个城市为唯一对应一个选择的点,所以一个非叶节点必须最多一个叶子,否则就不合法。
叶子的选择还好说,但是问题出在其父亲的,因为我不知道父亲可不可能选,我们考虑进一步发掘性质也发不出来什么,考虑父亲选择是很宽泛的,我们考虑能否强化限制,我们猜想叶子父亲究竟选什么,大胆猜想就是选叶子,证明考虑反证法即可。
然后就好说了,那么这两个节点的匹配方案是唯一确定的,我们把这两个节点同时删去之后得到一个新树,递归操作直到树为空即可,所以如果有解匹配方案也只有一种。这种方案我们如何考虑赋值呢,发现这个满足的是偏序关系,用拓扑排序确定顺序即可,时间复杂度。
总结:从一些简单结论入手,然后再考虑强化结论。树的构造从叶子入手已经老 old trick 了。
当限制过松的时候,我们可以强化限制,可以只考虑少部分的变元就能给出构造方案。直观上好像每个地方都能改,但实际上很多地方是“被迫的”,一旦你确定了某些关键部分,其余部分就自动唯一确定了。
CF798E Mike and code of a permutation
我想了 1 小时然后告诉我主席树优化建图喵了?
考虑到本题的限制都是偏序关系,我们要通过这些偏序关系来确定一个排列,这个是拓扑排序的拿手好戏。考虑用图论的建图来表示偏序关系。考虑顺序扫描中维护一个没有标记过集合。
- 若,对于 且,若 则令。
- 若,对于 且,若 则令。最后令。
暴力建边加暴力拓扑的时间复杂度是,无法承受,但是注意到这是一个动态删点加集合区间连边,可以用主席树优化建图,但我脑子没那么好所以想不到,所以先假设我不知道。
我们发现这样做是没前途的(哈?),因为直接光建图就是 了。我们考虑维护入度,但是发现入度很难降到 以下的复杂度进行维护。
考虑到限制是一个偏序关系,我们可以考虑不去维护入度,我们去维护最值。那么原来的拓扑排序图就不对了,但是我们可以通过建出原图的返图,让后枚举,如果当前遍历到的点没有被访问过就以其为起点在反图上 dfs,最后回溯的顺序就是拓扑序。
那么这个方法一个好处就是我们只需要知道图上连出去的点是什么就可以遍历了。具体的连边情况,设 表示 点被标记的时间,如果没有标记,为了方便。那么正常点(即)有两个边: 和 其中 且 即可,显然可以通过线段树优化建图。但是太麻烦了,我们不用真正维护出边,而是选出最有可能被遍历的那个点去更新它即可,我们可以转化为最值问题。具体的,对 为下标建出线段树,维护 的最大值,更新时找到 最大的 看是否满足,若满足遍历,否则无出边,时间复杂度。
总结:
如果不是计数问题,那么可以考虑把维护数量转化成维护最值。 维护最值当然是好做的啦。
这种 Dijkstra 的遍历思想大有用处,即如果每个点只需要遍历一次那么维护最有可能遍历的点.
CF827F Dirty Arkady’s Kitchen
哦我的天啊这是什么?
首先我们如何处理不能停留的限制。因为不能停留,所以要么在一条边上来回转,要么润去其他边。这对点是不好维护的,但是对边全很好维护,只需要分奇偶性记录第一次到达的时间即可,剩下奇偶性相同的时间都能到达。并且每条边能到达的时间点并在一起正好就是该点能够被到达的时间点,因而不会漏掉什么情况。
转移尝试模仿 Dijkstra,我们按照第一次走的时间优先队列,用每条边去更新目标点后面的边。
将点拆成奇偶两个点,每条边分别从奇到偶、偶到奇连两条单向边,共四条边。每个点把边按起始时间排序,加入一个边就将所有起始时间小于它结束时间的边都扔到队列里。显然之后的边不会让这些边的开始时间更优,因此可以在列表中直接删除已经加入过的边。时间复杂度。
本题难点不在于越早到某个点越好,考虑需要较晚到某一个点通路才开放,现有快路径和慢路径,可以先通过快路径到达这个点之后再在慢路径的最后一条边上来回横跳,这样可能达到和慢路径相同的效果。
总结:在有明显的时间戳的图论问题中,动态加边扩展是一个好方法。本题其实是用动态加边解决最小到达时间的问题(你可以理解成维护连通性的常见方法),然后维护最晚到达时间来判定这条边能不能用于扩展,本质就是两种限制的拆分导出了我们使用的方法。
P3573 [POI 2014] RAJ-Rally
还真是,每做一道难题就要去 zxy 上找点清淡的吃。
直接给你 DAG,这么好?考虑拓扑排序,那么得到拓扑序后有一删点最长路径的性质:
- 设删除点,那么删除点之后的最长路一定是拓扑序小于 和大于 的点路径。
可以考虑暴力预处理路径,但是枚举修改点之后就是 的了,题目要求的复杂度 我们只能再遍历删除点的时候进行计算。
我们可以预处理出经过每条边的路径最大值(正图和反图跑拓扑),然后类似扫描线,离开一个点的时候加入所有边到 set,询问之后删除这个点的所有边,时间复杂度。
总结:
删点后求最短路的问题有固定套路,就是考虑有一条边一定会跨过这个点,可以拼凑出路径来。
CF605E Intergalaxy Trips
首先战术上期望 DP,设 表示?哦不对,设 表示第 个点到 的最小期望步数,有转移:
这个转移很难泵,因为高斯消元不能直接消。但是我们发现每次我们肯定确定最小的 然后再去确定大的并且一旦确定之后它的值就不会再改变了。这个玩意很想 Dijkstra,考虑用 Dijkstra 的顺序来进行转移,然后每次转移找最小的 转移其他节点,时间复杂度。
总结:
如果转移的顺序是值,并且值大的不会影响值小的。那么可以用类似 dijkstra 的方法,每次取出最小值并且固定,考虑它对其他值的影响即可。
P7516 [省选联考 2021 A/B 卷] 图函数
由于全是和式而且还带删边,但是我们只需要算所有点的总和。我们只需要考虑单个点的贡献就可以了。
但是还不是太好考虑分析性质:
- 由于为有向图,所以肯定在强连通分量内才能算上贡献。
- 删点是从小到大按照编号顺序删点。
那么也就是说我们可以从强连通分量的角度来进行考虑,但是我们显然有一个问题,我们要动态维护 Tarjan 强连通分量,显然极难维护。但是我们发现删点是从小到大进行删点的,我们可以考虑 的贡献,如果我们保留 的点和有关边的时候,和它能够互通的 点个数,而根据第二性质我们不用考虑 的点因为已经被删除了,时间复杂度是。
然而搞笑的是有删边,但是发现删边是一个前缀,我们可以转化为反着加边。但是搞笑的是又遇到动态 tarjan 了,显然肯定不能做。但是我们思考我们是求的是和式,可以考虑固定点 求 的贡献,最后累加起来。然后我们思考这玩意是动态加边,我们要动态维护点的连通性,如何在不使用 Tarjan 的情况下动态维护?考虑 之间两个路径,如果我们固定点 必定是向外拓展的,我们可以考虑建出正反图,然后在这两个图上进行拓展,每次加边我们动态 bfs。果加入的这条边两个端点都访问过就没用,如果终点没有访问过就以他开始 bfs,每次把 bfs 到的边删掉,如果两个端点都没访问过就加入图中。每条边只会被删除一次,所以时间复杂度。
总结:当不用求出具体值,只用求总和时,考虑贡献法。动态加边还可以直接维护强连通性,对正反图动态 bfs 即可 P7516 [省选联考 2021 A/B 卷] 图函数 - 洛谷
CF1556G Gates to Another World
真的调不出来。
首先可达性可以转化为连通性,我们考虑如何维护连通性,冰茶几维护什么?
考虑题目给的这个 个点一定有它的性质,基本上离不开几个:线段树形态,二进制位表示等。
不难发现这个点连边我们可以用完全线段树的形态来表示,其中每个左儿子和右儿子的叶子节点对应连边,同时也不难发现线段树一个点所代表的区间内部是连通的。
但是搞笑的,有了删除操作就不好做了,注意到询问可以离线,直接一个战术时光倒流,将删点改成加点。我们给每一个点打上一个删除标记 表示删除这个点的时间,如果没有删除则,然后通过线段树结构来进行优化连边。搞笑的,这样做时间复杂度是 因为我们要先把所有节点的预先建出来,但是我们没有很好的利用这个叶子节点连边和点内区间联通的性质,注意到一个"叶节点"(并不是真正的叶子,而是动态开点之后没有儿子的结点)中所有叶节点的行为平行,因为它们删除的时间相同,并且一定联通,所有可以把他们当成一个点来考虑。
那么这样复杂度正确,于每个非叶节点一直递归下去,直到找到两个叶子连边,这条边被删除的时间是 ,求出所有边之后我们离线逆序加边,用并查集判断连通性即可。时空复杂度均为。
总结:
这是一个对应点优化连边问题,这个优化建图无法用常规的优化,一般的做法是用数据结构维护某个量,读入所有修改后再优化建图。
对于带修改的问题来说,可以有一个统一的固定结构来处理两点连通的时刻(边起作用的时刻)
P7056 [NWRRC 2015] Insider’s Information
随机化过于人类智慧故不讲。
首先考虑如何判断一个三元组是否合法,有一个必要条件就是 必须比 或 先插入,否则一定不合法。
剩下的,我们还需要确定 之间的偏序关系,这种确定偏序关系的我们可以考虑利用拓扑排序来去求解。考虑先建边来表示必要条件,那么有两个: 和,但是发现你不可能确定两次,故我们可以让 b 的入度只增加 1 即可。这个操作很不好笑。
然后我们就有了一个合法的拓扑序,至于为什么合法因为题目没有给出无解该干什么所以一定有一个合法的拓扑序。我们可以利用这个拓扑序来决定每个数是放在最左边还是最右边,考虑 三元组在拓扑序上会呈现 4 种情况:
- ;
- ;
- ;
- ;
考虑到后两个和前两个是对称的,我们可以对前面两个单独进行考虑。我们思考两组什么时候会产生贡献?
- :产生贡献当且仅当 在最左侧。
- :产生贡献当且仅当 在最右侧。
剩下两组也是对称的,这说明:我们只需要在将要加入第二个元素的时候考虑这个限制。实现的时候我们将拓扑排序的决策同时进行,我们分讨是作为 的限制和作为 的限制(对应 已经插入)即可统计放在最左边和最右边的贡献,放较大的即可,由于每次都是少的往大的放,满足限制至少有 个,时间复杂度。
总结:这个贡献其实很巧妙,我们首先通过拓扑排序来确定顺序,然后将三元组的限制放在单点上来去简化问题。这种操作的前提条件需要我们先拆分限制简化条件。
类似的:#2999. 「JOISC 2015 Day2」Keys - 题目 - LibreOJ
9月
CF1062F Upgrading Cities
拓扑排序练习题,但没有完全理解拓扑排序。
考虑这玩意就是一个可达性,你在正反图上跑一个 bitset 统计可达性就可以简单做到,但是不用猜都知道这个做法会被卡。
考虑优化,我们需要知道一个性质就是 DAG 上的拓扑排序,队列内的点是互相不可达到的,这个证明是显然的。所以我们可以通过分类讨论,设队头为 且此时未弹出队头元素, 表示已访问过的点数:
- 若队列大小为,即只有。那么显然满足第一个条件可到达的点为。
- 若队列大小为,即有 又有,为了满足第二个条件我们考虑遍历 的出边,若一条 的出边,但 的入度为 1 则显然不合法。反之则到达点位。
- 若队列大小,两个条件都不合法。
在正反图上遍历即可,时间复杂度。
总结:同在队列里的点没有任何到达关系,可以通过它来筛选合法点。这个我是真不知道很搞笑。
AT_agc036_d [AGC036D] Negative Cycle
P5664 [CSP-S2019] Emiya 家今天的饭
哈!
这个 的限制很难处理,因为组合很难直接去做,考虑正难则反,我们将 转为求解 的,我们发现由于 的 是总数,那么 的列有且仅有一个。
考虑枚举法确定我们的决策列,然后我们计算方案数,然后我们用总方案减去不合法方案即可。
考虑 DP 求解,设 表示前 行,选了 个点,当前枚举列选了 个点的方案数。转移枚举即可,时间复杂度 只有 84 分。
考虑优化,发现我们的瓶颈在于第二维,先猜想第二维是否状态数量上限,发现 很炫猜都不用猜,我们考虑能否去掉第二维,发现我们状态的表示只需要确定 的限制是否满足即可。考虑分析:
故 DP 直接去掉第二维,然后维护差值,设 表示前 行差值为 的方案数即可,时间复杂度。
总结:以后看到这种具有 的限制可以思考正难则反,对 先进行思考,因为显然 至多出现一次。
DP 在优化状态的时候,我们不仅要思考谁是瓶颈状态,还要思考导致瓶颈的原因是什么,才能更好的进行优化和发掘性质。
P4769 [NOI2018] 冒泡排序
众所周知的是,冒泡排序的交换次数就是排列的逆序对数。
首先不考虑字典序(即特殊性质),我们如何计算有多少个排列满足逆序对数等于。我们考虑原式子为,变形有,其中后面的式子我们考虑用图论刻画,即 进行连边,那么 就表示跨过的距离,那么合法当且仅当每条边穿过的格子正好对应它参与的逆序对的个数,即所有逆序对两两配对成边的端点,且没有多余交叉。
也就是说,逆序对必须两两配对,不可能出现一个位置被两个人抢走配对的情况。
等价的转化提议,即不存在三元即以上的序列满足 使。即不存在三元即以上的下降子序列。
那么这样如何刻画呢?我们发现这玩意由于没有一元子序列这一说法,那么必定为二元下降子序列,我们用图来表示合法序列数变化这一过程:
我们发现拐点必然是当前时刻序列的最大值然后接一个较小值,然后再继续上升。
故有一个 DP,设 表示前 个数构成的排列最大值为 的方案数,转移为,要求。这玩意是搞笑的,但是不难发现这玩意就是格路计数但是有 的限制,可以转化为卡特兰数,可以 计算,或者公式为。
现在考虑有字典序的限制,这个限制我们可以转化为至少一个位置满足,其余任意。我们考虑枚举法确定这个位置什么,我们钦定一个位置,前面的和 一致,第 个必须大于。令, 为最小可以填的数。
由于我们强制钦定之后从 的 的计算就不再适用了,我们将其定义为从 走到 的方案数。
接下来我们考虑如何计算方案数,考虑分类讨论:
- 若,那么我们显然只能填写 的方案,即。
- 若,显然只能填写,但是显然这样构成不合法排列了,故无解。
- 若,只需要填写一个 的数就可以了,即。
时间复杂度。
总结:通过将公式转化为清晰易懂的方式,如本题的图论和坐标系表示变化。这是常用的技巧,通过不断简化问题,我们才能发掘一些好玩的性质。
同时给出了 DP 优化一种新思路,通过 DP 式子的组合意义来进行优化,有的时候可以大幅降低复杂度。
本题目放在卡特兰数是有什么心事吗?
AT_arc139_d [ARC139D] Priority Queue 2
好练习题!
我不知道为什么我的题面是让我算期望,但是问题是等价的。
有 个数,接下来进行 次操作:随机一个值域在 的数加入,然后删掉第 小的数。其中 给定。
问 的期望,对 取模。
。
先考虑简化问题,我们考虑值域为 的情况下如何去做,那么显然每一次加入是等概率随机选取 加入,如果 的个数超过 的话我们就要把它删掉, 我们不用管因为答案求的是 的个数的期望,贡献答案的只能是。
由于 一开始给定,选择给定,答案贡献只能由 贡献。故我们可以枚举 次操作一共放了多少个,用组合数算一下就可以了,具体的就是枚举 个数,答案为,其中 为:
其中 为题目中给出的删除阈值,即。时间复杂度。
现在考虑到值域扩大到 如何去做,注意到这个第 小我们只需要关心相对大小即可,我们枚举权值,序列可以转为 序列,大于某个权值设为 ,否则设为 。这样转化后的命题是等价的,因为期望具有线性性,有。只需要枚举权值,将 的数设为 ,否则设为 。将所有上述问题的答案和相加即可。只需要做 遍上述过程即可,时间复杂度。
「JOISC 2017 Day 1」港口设施
先考虑简化问题,即我们只有一个栈的情况下什么时候合法,我们将每一个元素的入出栈时间看作一个时间区间,那么合法的充要条件就是所有区间要么包含,要么独立,不能交。
有了这个判断条件好说了,有一个性质就是由于这两个栈都是独立的,所以我们可以通过选取区间分配到两个集合中,求有多少种合法的分配方案。说人话,求出有多少种二染色方案,使得同色的线段不交。我们把区间看成点,对于相交区间 和,满足,我们让 连边,然后我们求这张图的连通块个数,由于连通块内必定是黑白交替染色,故确定一个开始色即可,一个连通块贡献 个方案,答案就是。
暴力连边求解是 的,无法通过,而且问题在于这些区间点属于散点没法硬上线段树优化建图。我们考虑按右端点从小到大扫描所有线段,每次维护右端点更大的线段组成的集合,那么当前点连接的点必定是 中的一段连续区间(左端点在 中的点)。
但是发现这样做还是会 的很搞笑,看起来很难做了。我们继续发掘性质,发现一段区间被连接后的效果是,区间中的点必然同色。所以维护 表示与 同色的点最多延伸到哪里,那么修改变成暴力访问一段区间,并且把这段区间的 全部指向区间的右端点。这个复杂度看起来不对,但是我们通过冰茶几路径压缩的复杂度来进行分析发现这玩意是对的,时间复杂度。
总结:二分图染色问题,如果需要优化连边,得到同色的性质可以缩成一个点,然后套用并查集路径压缩的时间复杂度。
CF1396E Distance Matching
CF1387B2 Village (Maximum) 做过吧?严格加强。但是我做不出来。
对于这种构造可行解使得权值和恰好为某一值的题,一般都是先求出可以构造出来的最大和最小值,然后从某个极值按照一定方法进行连续修改。
我们考虑剖叶子来描述上下界,但是剖叶子很难确定匹配问题的选取,但是注意到贡献是树上距离。这种树上距离我们可以考虑拆分贡献法,将点对之间的贡献拆分到边上。
我们考虑一条边 的贡献,那么很容易得到一条边贡献 的上下界,即为。即子树尽量自己内部匹配和尽量跨边匹配。
考虑到 是难受的,有一个 Trick 就是我们可以通过取重心为根就可以去掉子树 的式子,那么贡献上界 就是 下界 是。
我们考虑必要条件,由于,更换点的匹配只会引起 lca 这一项的变化,所以无论如何边权和的奇偶性不变。所以必要条件为 且,我们考虑给出充分性证明,显然只能构造了 www:
考虑到边权和为 我们接着调整到 的方案,开始可以把 dfn 序为 i 的点和 dfn 序为 i+n/2 的点配对,这样是能构造到 mx 的(下文称之为初方案),而且所有路径都跨过重心,我们在构造时考虑维护根为重心的这个性质,所以我们选取点数最大的子树来操作,设 y 表示最深的非叶节点:
- 如果 ,我们直接拿 配对(优先儿子,可以自身),那么配对后相较于初方案的边权和会减少 ,配对后删除这两个点,树的形态不变,我们在新树上构造出新的初方案。
- 如果 ,因为 dep 连续这一特点,我们找到 ,然后类似于上述方案配对即可,边权和会减少 ,这说明我们找到了答案。
如果还有未匹配的点就按 CF1387B2 Village (Maximum) 的方法来构造即可,用 set 维护即可,时间复杂度。
总结:
从一开始提到的本题两个,我们总结出一个构造思考路径:对于这种构造可行解使得权值和恰好为某一值的题,一般都是先求出可以构造出来的最大和最小值,然后从某个极值按照一定方法进行连续修改。
同时还能总结出,对于树上遇到 的式子的时候,可以通过取重心为根的方式来去除。
同时这是第二次对于树上路径和问题的贡献法应用。
CF526G Spiders Evil Plan
最速通的一集。
先考虑分析性质,我们发现使用 条路径就可以覆盖一棵有 的叶子的树,证明是显然的。其次,我们为了最大化路径一定会选取叶子到叶子的路径,而且一个最长的路径一定会涉及到直径,这种最长路径问题我们可以考虑往直径上面去想。我们思考,若一棵树以直径端点为根,那么树将会长这样:
我们通过这个进行分类讨论:
- 若 点在直径上,那么一定有一条路径选择的就是直径,剩下的通过拼凑一对黑色路径贡献,取 个就可以了。
- 若不再直径上,那么必定 在直径延申出的一条分支(图中的黑线)上,那么从分支一端( 子树中最深点)为起点走到直径后拐弯往更远的直径端点走,剩下的继续拼凑更长链。
通过反证法和前面的路径不难证明上述就是最优方案,但是问题在于上面这玩意光是叶子到叶子的匹配是 的无法通过。考虑到这个最优方案有什么性质,注意到直径的最远一端必定作为答案出现。考虑枚举法,说人话就是枚举作为答案选取的直径端点,然后以其为根建树。
接下来我们需要求除直径以外的最长链,考虑到除直径以外的最长链必定为:黑段 -> 部分直径 -> 黑段。
由于直径显然是必选的,所以直径不会贡献答案,我们只需要两两配对最长黑段就可以了,由于使用 条路径就可以覆盖一棵有 的叶子的树,直径贡献 个叶子,我们只需要求前 长的支链配对就可以了,怎么求,用长链剖分。
哎不对啊, 的限制呢?考虑答案,如果在直径上就结束了。如果不再直径上那么方案必然为 子树中最深一点 -> 黑段 -> 部分直径 -> 黑段(若 则为直径端点),我们只需要将选取支链集合中贡献最小的替换掉即可。
直接做,时间复杂度是。
总结:
边权和贡献最大问题可以往长链剖分这个角度考虑,如果是路径问题可以通过 2k 个叶子的构造性结论转化成最长链问题(前提是需要定根),同时以直径端点就可以通过上面的思维模型来辅助思考。
P5327 [ZJOI2019] 语言
第 75 黑。
好题?
考虑树是一条链是怎么做,我们可以维护每个点为左端点最远覆盖到的右端点,用线段树求区间最大值然后把所有位置的贡献求个和即可。
考虑暴力的 40 分怎么拿?显然 的暴力对每一个点维护 set,然后 的对于每一个点计算向外搜子树内能拓展到的点,设其数量为,那么答案就是。很好,现在你有 60 分了。
然后怎么拓展,考虑到我们不能暴力向外拓展,我们能不能将链的做法和暴力结合起来?考虑到路径必然是树上连续点集所构成的,所以一个点能到达的所有点恰好构成一棵生成树(即一个连通块)。
我们考虑这个生成树如何构造,发现如果路径 包含点 , 则是 的两个极远点。而 的生成树则是连通所有 的极远点的最小生成树。
肯定不能真的去求这个生成树,能否巧妙地计算出生成树大小?考虑点集,我们加入一个点,那么最深的,其中。那么 的贡献就是,这玩意很像虚树,有一个 Trick 就是将所有点按照 DFN 排序之后,其中 表示上一个加入的点。注意第一个加入点的贡献并不是它的深度,而应该减去最上面联通点的深度,所以可以先记贡献为 ,最后再减去 ,这里的 是指的所有点的 LCA。
剩下一个问题,如何取出经过了这个点的路径,由于只需要计算一次答案,考虑树上差分即可,即在端点加入路径贡献,LCA 以及 处删除贡献。
加入点的问题可以用线段树维护,线段树的下标需要按 dfn 排序,上传的时候减去左儿子最右边的点和右儿子最左边的点的 lca 的深度即可,然后线段树是支持标记合并的,所以写个线段树合并就行了,时间复杂度。
总结:
要快速计算虚树的大小时,可以考虑下标为 dfn 序的线段树来维护。
Ridiculous Netizens - HDU 6643
This is the true 好题!
首先你会想到用树形背包来做,但是问题在于如果你直接设置为 表示为 子树内乘积为 的方案数,但是直接做会出现两个问题:
- 你无法保证你选取的方案子树是连通的。
- 在不考虑乘积的情况下,你的合并是 的,因为你要枚举约数。
先保证状态是,然后我们考虑把第一点解决掉,第一点的问题就是在于我们一般树形背包是自底向上合并的,但是这样可能中途就会断掉。转化思路,我们可以确定一个子树的根,然后从根自上向下贡献答案,说人话就是我们可以把原命题转化为一个单点加入问题,选取一个点就说明必须选它的父亲。这玩意是在 DFN 序上 dp 的过程,因为 dfn 特性,子树 dfn 序连续,考虑在 dfn 上进行 DP。但是显然实际实现肯定不能直接暴力求出 dfn 序,设 表示 内加入点的构成的子树,乘积为 的方案数,转移首先自上向下贡献,然后递归完子树后用儿子的答案更新当前点的答案即可。时间复杂度是 的。
然后考虑第二个情况,我们不考虑乘积暴力合并是 的,我们的目标是要优化到 的状态。看起来很难做,考虑发掘性质,注意到我们枚举约数中使得 的时候,所管辖的区间有很多重叠的部分,同时又注意不到,,可以用整除可以把 整除 的值定义到状态里面。根据整除分块状态数变成,根据结论值相同在以后的转移方法也相同所以正确性得到保证。
但是这是无根树,每个根的过程是相对独立的所以不能一遍求出,且合并子树是,但是插入点是 的可以承受,考虑点分治减少子树大小,即可优化到。
总结:不支持合并的树上问题可以考虑转成 dfn 序上 dp,同时这种等价类的优化方法我也是第二次?见了,通过整除分块让状态数大幅减少(整除值相同的划分为等价类)。根独立的 dp 问题可以考虑用点分治优化,原理就是缩小子树中的需要考虑节点数。
CF611H New Year and Forgotten Tree
nm 就给我给位数是吧。
考虑到这玩意实际上是给边分配点,同时不难观察到同位数的点它们是等价的,因为都要分配同位数的点。
考虑到同位数之间的边是容易的,因为我们可以显然把同色的点缩成一个块,但是不同位数连边是困难确定的,所以我们首先确定不同位数连边。我们考虑枚举法,钦定颜色代表点把这些代表点做生成树,剩下的点接在这些代表点上,这是因为如果存在解,那么就存在其他点之连接代表点的解。证明可以用反证法和调整法证明。
因为颜色数极小,可以考虑枚举 Prufer 序列来确定代表点之间的生成树,然后把每个颜色的点放在一起考虑,边 可以通过和颜色 j 关键点的连边解决一个颜色 i 中的点,也可以通过和颜色 i 关键点连边解决一个颜色 j 中的点。这玩意是一个二分图完美匹配问题,可以通过网络流或 Hall 定理来判断是否合法并构造最优解。
总结:这个细节不在于观察到等价,而是在于钦定代表点这个环节,对于还原树的问题中,可以分步还原,也就是先还原特殊点的结构,再还原整体的结构。
CF1984F Reconstruction
这玩意前后缀和,首先我们先思考一个确定的序列什么能够判断合法。首先这个前缀和和后缀和太难受了,我们考虑转换成统一的,不妨令 为前缀和 为后缀和,那么显然。只要不出现 即可,对于这个的贡献是相邻两项所贡献的,可以对相邻两项分类讨论 4 种情况即可。考虑强化限制,只要我们知道 的情况下我们就可以通过 DP 求出满足限制的方案,时间复杂度。
考虑我们不知道 的情况下怎么办,这种情况我们需要知道能够唯一确定 的信息,注意到令,, 之后,任意意一个 PS 子串都可以决定,而显然至少存在一个这样的子串所以可以唯一确定,暴力枚举每个可能的 计算 的数量即可,时间复杂度。
总结:这种部分不确定性的问题,我们需要思考其中确定的信息,通过这些确定的信息去确定其他的不知道的信息。
AT_arc165_e [ARC165E] Random Isolation
大技巧题,我不会的技巧都叫做好题好吧(逃)
首先一看这玩意 “在剩下的点里随机选一个”,操作概率的分母一个一个都不一样。这种随机操作求期望的问题一般情况会出现在这里,这种情况下我们可以对于一个随机过程,可以考虑将所 有元素钦定优先级来刻画。 钦定优先级会将一个问题限定在离散的范围内,一些不同情况下 不好计算的概率在钦定优先级之后可能会很好计数。
对于这个题,我们转化问题,转化为对于随机长度为 的排列,我们按照 的顺序依次考虑,若 所在连通块大小大于,那么再当前树上删除;否则不进行任何操作,求有效操作的期望次数,忽略掉所有无效的操作之后,这个命题和原命题是等价的。
考虑能否对每个点计算共享,考虑删掉点的时候的连通块,显然它的大小需要。 既然这样,这之前对该连通块内点的操作显然全部需要成功。 因此,我们甚至可以假设所有这之前的操作都成功(因为即使切到别的连通块也不影响这个连通块的大小)。
那么有 DP,设 表示 子树内,有 个点被删了,根节点连通块大小是 的方案数。时间复杂度。
这是权值,最后还有概率要乘上,对于原树中一个以 为根,大小为 的连通块,他能造成贡献,当且仅当与这个连通块相邻的 个点全部在他之前删除。剩下的点对他没有影响,所以只要考虑这 个点即可。产生贡献的概率是好算的,随便排是 种, 个先全删的有 种,概率为 。
总结:
学到了一种随机过程期望的方法,就是将所有元素钦定优先级来刻画。 钦定优先级会将一个问题限定在离散的范围内,一些不同情况下不好计算的概率在钦定优先级之后可能会很好计数。
【UNR #1】火车管理
最快的一集。
考虑到操作 2 才是最 nb 的。显然不能每一个栈都去维护,5e5 让我们只能考虑一些 polylog 级别的数据结构,考虑线段树维护栈顶,但是问题在于弹栈,我们发现删除操作,可以看成回退到上一时刻,可以用保留所有历史版本的主席树来支持回退。你需要做的就是维护覆盖这个单点的时刻,然后修改单点查上一时刻的值,用这个值修改即可,时间复杂度。
总结:删除操作,可以看成回退到上一时刻,可以用保留所有历史版本的主席树来支持回退。
CF1651F Tower Defense
我知道分块的 简单维护颜色段做法。但是我是来学主席树的 QwQ
考虑分析性质,发现如果只有一个怪物的情况下那么销毁的必定是一段前缀,但是如果怪物多起来了就会将序列分成一段一段,每一段的数值状况不一致。启示颜色段均摊,但是显然这个不是拿 ODT 维护的。但是我们可以拿个栈存一下每个段的分界点,按照左端点降序排列,询问时类似弹栈即可。
然后我们考虑原命题的限制,其中 为怪物到来的时间差,我们可以把他看作一个分段函数,即:
考虑到一个段,我们如何判断当前的怪物能否清楚这个段呢?只需要看当前生命值 是否满足 即可,当然如果 直接 做就可以了,但区间求和考虑使用线段树来维护一次函数,但是分段函数如何维护呢?注意到值域是较小的,我们可以用可持久化线段树来维护这个分段函数,具体的,以自变量 为版本,线段树维护每一个,修改只需要在分段的地方单点修改即可,预处理的时间复杂度是。
现在我们能判断能否一次清楚这个段了,但是如果无法清除那我们怎么维护呢?分析问题实质上就是我们需要求出我们能够清楚这个段最长能延伸到什么位置,可以考虑主席树上二分去求出这个位置,那么 和 就是旧段操作后的新段,直接维护,时间复杂度。
总结:维护分段函数,在值域较小的情况下,我们可以通过可持久化,以以自变量 为版本,线段树维护每一个。
CF679E Bear and Bad Powers of 42
首先不难观察到 的值域在题目范围内是很少的, 取值在。
其次第一个操作第二个操作是容易的,但是第三个操作是不容易的,因为是连续操作,而且我们要维护的是加法中触碰到特定值的部分。考虑到特定值的数量很少,我们有一个想法就是类似于树套树,外部为正常维护序列的线段树,内部为权值线段树,每一次枚举权值,查询是否有 的值存在,若存在则继续累加,直到结束。显然这个做法看起来很可以,但是内存会炸。
考虑这个做法能否优化,首先观察到我们每一次查询都是只需要查每一个权值 是否存在,但是我们记录所有权值的情况太过于浪费空间。我们思考,对于一个序列数,加法能影响到的只能是 的。有一个想法,我们对每一个 维护到下一个 的距离,如果有数的距离 为,那么就再次进行操作 3 直到不为 0。
具体的,我们需要在线段树维护这个区间距离最小值,操作 2 可以暴力区间赋值。但是操作 3 是个问题,因为我们暴力修改每一个显然是不行的,但是注意到若一个区间距离最小值 是可以通过打标记 做,若不满足就暴力递归下去,借鉴 Segment Beats 的势能法分析是可以的。我们不妨定义势能为:区间所有颜色段上方的 42 次幂个数之和。一次操作 2 会增加 的势能,操作 通过 时间减少 势能,时间复杂度。
总结:线段树上尽量不要去维护有关特定值的信息,如果需要维护常常可以通过放宽条件的方法解决。例如本题放宽为了考察区间中所有越过 42 次幂的数。
【UR #19】前进四
哦我的天啊这是什么?
首先考虑,首先这玩意可以转化为从后往前的极长下降子序列的长度,这玩意是 LCIS - HDU 3308 - Virtual Judge,可以使用我们的线段树理论简单构造出信息!
然而这玩意是区间求的,我们求得是一个后缀,如果用维护区间的去维护后缀就太浪费了。注意到题目可以离线,考虑离线,离线之后我们就可以考虑类似扫描线一样的后缀扫描,依次扫描询问,维护每个位置的数据结构。但是我们发现这玩意和上面做法没有什么差异,考虑变化主体,从后往前依次扫描位置,维护每个询问的数据结构。
我们把所有东西离线下来,那么修改变成了对一段询问区间取 min,询问变成了对于某个询问单点求 min 值的变化次数。用 Segment Beat 维护即可,时间复杂度。
总结:先弄清维护的信息是什么,然后切换主体,保持维护信息的不变即可。通过离线我们可以方便的切换主体。
CF1017G The Tree
神秘主体思想。
考虑链怎么做,显然不难发现原命题相当于黑色段和白色段,一个拓张,一个缩小,同时会有区间推平为白色操作。可以考虑分块维护颜色段,时间复杂度是。
考虑放到树上怎么做,发现这玩意很抽象,因为如果我们暴力维护段的话直接就 T 了,考虑到如果对段暴力拓展显然是没有前途。有一个性质就是段拓展只会向下拓展,考虑到询问只有单点查询,我们考虑一个点什么会被变黑?上面的结论推论就是一个点若会被影响到当且仅当其祖先中操作次数足够到可以将范围扩大到影响当前点。
进一步转化,我们将每一个点权值初始设置为,对于操作 1 在该点上进行单点加,那么单点查询时,为黑当且仅当当前点到根的链最大后缀(从当前点开始)权值和,即距离能够够到,否则为白。
转化成 DFN 序上,用树剖加线段树维护,发现这玩意就是一个最大后缀和,可以直接用线段树维护,时间复杂度。
总结:
本题目的精华就是在于将这个操作等效,等效操作的思想是很重要的,当你切换维护对象之后,可以通过等效操作来适应现在所维护的东西。
P7735 [NOI2021] 轻重边
考虑分析性质,注意到每一个重边路径段都是互相独立互不干扰的,由于操作首先会将相邻边都变成轻边然后再变成重边。然后我们考虑怎么维护这些重边路径段,而且还要满足独立性,我们发现这玩意可以直接转化为维护边上的颜色段。
显然边上的颜色段不好维护,我们考虑边权转点权,那么我们给颜色段内的点赋一个颜色,这个 要满足每个颜色段对应是唯一的,那么是重边当切仅当。
树上路径带修我们考虑树剖,然后转化为为 DFN 上的区间问题,然后线段树维护即可,时间复杂度。
总结:属于染色模型,一些类区间赋值类操作可以向染色模型转化。
呃呃呃。
CF1458C Latin Square
啊啊啊。
首先观察到所有操作全是全局标记,维护整体标记,本题的核心是考察整体操作对单点的影响。
发现前四个操作对于单点是独立的,我们可以维护偏移量。但是问题在于后两个操作,后两个操作单看每个元素的位置变化是混乱的。
我们考虑能否独立化这些操作,考虑转化问题,我们转化到三维平面上,有 个坐标,对行取逆就是交换坐标的第二维和第三维;对列取逆就是交换坐标的第一维和第三维。那么我们再维护表示维护交换的整体标记即可,时间复杂度。
很好的题啊啊啊啊,如果我们想要维护整体标记,我们要考虑整体操作对于单点的影响,把整体操作对单点的影响独立开来,分开维护,查询单点时,把操作一一作用在该点上,得到真实答案。
P3352 [ZJOI2016] 线段树
需要把这些序列大小要整合到一起,不然不知道用什么处理?
笛卡尔树?bro 有点难。咱们还是考虑 01 序列怎么做吧。
首先没有概率,就是纯纯的求方案数乘上权值。考虑值域为 的时候怎么做,不难发现对答案造成贡献必定是 段和 段合并,并且发现 段必定会被 段给包夹(边界位置设置为)。考虑到每次操作 段大小单调不降, 段大小单调不升,我们考虑 DP 主体应该为 段,有状态 表示 操作后 段缩小到 的方案数,有转移:
不难发现可以用前缀和优化转移,时间复杂度,拓展到一般序列上我们把 的贡献拆为,即把所有 的位置标为 1,把所有 的位置标为 0。此时我们就可以算出每一个位置 的方案数,时间复杂度,数据随机可过。
显然太吃运气了,考虑优化,发现所有的 dp 值的转移柿子都完全一致,所以我们可以把所有初始值放到同一个 dp 数组里面,然后进行一次整体的 dp,就可以求出答案。
总结:01 序列天地灭!
P5443 [APIO2019] 桥梁
刚开始做操作分块,不太熟练。
考虑到这玩意显然不太好 polylog 去维护,基本上稍微复杂一点的都没法polylog?
首先可达性转连通性,问题转化为维护连通块内点个数,我们首先有一个显然的想法就是修改就暴力修改,对于每一个询问,在并查集中加入所有 的边,时间复杂度。
考虑没有修改操作的时候怎么做,注意到可以离线,考虑离线所有询问,然后按照 从大到小排序,每次加边用并查集维护连通性和来连通块内点个数,时间复杂度是 的。
但是现在有修改操作,如果我们还是仿照以前的做法的话我们需要使用可撤销冰茶几,对于每一个 我们都暴力扫一边询问然后计算贡献,处理完每一个询问的时候,再撤销掉临时加入的边。时间复杂度是,瓶颈再修改。
考虑操作分块,每 个操作分一块。注意到每一块内修改边权个数不超过 个,询问次数同理,因此考虑对于不在该块内修改的边,直接固定边权。和上面的做法一样,还是考虑离线询问按 从大到小,但是我们只用离线当前块内的询问,对于每一个询问,看看在该块内修改的边,在这个询问时权值分别是多少,然后加入 的边,询问连通块个数,然后撤销临时加入的边。
最后将新操作修改的边更新到原来的边上,相当于操作分块继承以前的贡献。时间复杂度令 可以取到。
CF1588F Jumping Through the Array
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊???????????根号??????????????????????????
操作没有任何营养。考虑最没有营养的操作 3 去掉怎么做。发现如果是单点修改那就很好说,但是问题是区间修改啊啊啊,没法 Log 维护啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊。
考虑发掘性质,但是没有性质啊啊啊啊啊啊啊啊啊啊啊啊。
啊啊啊啊啊?根号!考虑到所有操作全是 级别,我们考虑操作分块,每 个操作分成一块,我们发现对于每一个需要修改的位置,从它到它后边第一个需要修改位置之前的所有位置的 都不会发生变化,所以我们可以将这些位置缩成一个,这样环长就是 级别了每次可以暴力遍历。而每次预处理要花 来缩点,其次对于 1 操作我们可以查询修改的位置所造成的贡献,就是对于这些点上打标记,存下来应哪些点,然后每次二分出这个缩后的点里面有多少个点在询问的区间里,时间复杂度是 的,然后做完了?
总结:这 tm 什么玩意啊,操作分块这么神奇的吗?以后遇见这种图上神秘操作且 10 分钟内发觉不了性质直接开始想暴力,今天 byd 一个性质都没有,搞不搞笑。
CF840E In a Trap
首先注意到这个玩意如果直接对整体维护显然是没有什么很好的性质的,但是有一个极其关键的性质就是,由于位运算在二进制位下是独立的,我们不妨考虑按位分治,就是值域分治,分成前八位和后八位,那么值域最多只需要处理 即可。
然后我们考虑将询问点分块,说人话就是将树上以链分成 长度的块,前 8 位我们可以用 Trie 来预处理然后询问时查询即可,后 8 位我们需要处理,设 表示 向上的 256 个节点中最大的,查询可以先跳整块再跳散块。但是显然不能这么直接合并获得因为前 8 位也是一个限制,考虑设 表示前 8 位为 最大的,这样就可以合并了,时间复杂度时。
总结:看到 之类的限制多半要用到值域分块,对于加法和异或的混合问题可以考虑对半拆位。位运算和四则运算混合在一起是很恶心的,方法基本上只有按位考虑。
[AGC002D] Stamp Rally
翻译全部错误 666.
最大编号尽可能小,考虑二分。问题转化为求经过边编号 的 路径上点数量,将边权设置为边的编号,那么命题关系求两点路径最大权值最小值,容易想到 Kruskal 重构树,且这题限制了经过点的个数要恰好为 ,不能大也不能小,所以二分是一个比较好的解决方案。时间复杂度。
总结:大/最小边权问题考虑 kruskal 重构树。
P3684 [CERC2016] 机棚障碍 Hangar Hurdles
先考虑我们初始点最大能放多少,由于是一个正方形,我们考虑前缀和预处理这个网格图,然后二分求出最大长度。这样我们就能得出每一个点所能容纳的最大正方形长度。利用这个 我们对于正方形每一个点向四周连边,边权设置为,那么命题转化为求起点到终点的路径上边的权值最小值的最大值,用 Kruskal 重构树即可解决,但是为题在于连边过多,我们考虑对于 相同的点缩点即可,时间复杂度。在实现细节方面,我们注意到,由于障碍的存在,所以可能最后得到的是森林而不是一棵树。考虑到树与树之间是不连通的,所以我们完全可以新建一个节点连向这些树,并把点权设为 0,就可以直接按照普通一棵树的情况来做了。
码力题不写。
AT_arc098_d [ARC098F] Donation
牛牛牛
首先不难发现一个性质就是如果我们在某个地方给塞钱了之后我们肯定之后就不回来这里。同时发现答案必定,考虑到给钱很难想,正难则反考虑倒着走领钱,设,不难发现题目的条件就是要求满足到达点 的时候满足,如果不满足就补充即可。如果是第一次经过令。
这玩意怎么做?考虑最小生成树,令边权为,表示经过这条边当前钱数的最小值。但是我们发现这玩意很难搞,因为边权是乱序的,如果暴力枚举起点走的话是 的,但是我们发现我们肯定是贪心的走边权最小的。考虑这玩意我们可以在建树的时候求得,考虑 Kruskal 重构树表述建树这一过程。然后再树上 DP,设 表示 子树内都经过后最小领到的前,叶子节点即为,对于非叶子节点枚举从哪里最后进入出来即可,有。其中 表示 为根的子树内节点的,由于重构树显然是二叉树可以直接展开,但是如果你写多叉树那我没啥好说的,时间复杂度。
总结:本题通过发掘性质将这个不塞钱操作简化问题,同时正难则反是重要的思维技巧。
借助 Kruskal 重构树,通过合理的赋值边权我们可以满足题目中的限制,难点就是在于我们如何发掘边权所表示的意义。
CF1628E Groceries in Meteor Town
首先看到简单路径上求经过边权最大值不难想到利用 Kruskal 重构树,查询操作就转化成了重构树上, 点与所有关键点的 lca 的权值。
那么现在为题转化为如何求一个点集合的 LCA,如果你做过树上查询你可能会以为是区间 LCA 直接一个一个维护,但是显然不是这样的,这是点集不是区间。答案是点集中 dfn 最大点和 dfn 最小点的 lca,所以直接维护区间最大最小 DFN 即可。
总结:学会了新的 LCA 方式!求一个点集合的 LCA 答案是点集中 dfn 最大点和 dfn 最小点的 lca。边权最大最小问题考虑 Kruskal重构树。
P3679 [CERC2016] 二分毯 Bipartite Blanket - 洛谷
呃呃
注意到,考虑状压选取的点集合,但是我们只能状压一个不能状压另一个,如果直接做将会达到 无法通过,复杂度启示 也就是说我们只能状压一个点集,考虑到我们还没有分析性质,分析性质。
现在的问题就是我们只能状压二分图中一部的点集,考虑到上面算法的瓶颈在于我们必须知道我们和哪些点匹配了。联想到 Hall 定理可以帮助我们在只有点集合大小的情况下完成匹配,题目要求就是两个选取出来的点集 和 有完美匹配,但是点集合大小我们只能知道一个集合的大小,如何推出是否有完美匹配呢?
考虑拆分法,由于二分图两部点之间是独立的,我们只需要算一部的选取点集合所有点匹配(如果存在无法匹配我们可以去掉,这个状态在之后一定会枚举到),这种情况下是否能够凑出 即可,那么根据 Hall 定理不难发现一个结论:由于点集要求全部都选,而且只要求一个匹配覆盖即可而不是点集之间两两覆盖,那么也就是说点集合只要能够完美匹配即可。而对于左部点集 和右部点集,只要两者 和 都对其能够到达的点完美匹配即可满足两者必定存在一个匹配覆盖。
考虑证明必要性:显然若有覆盖 的匹配,显然能分别覆盖 和。充分性: 与覆盖 的匹配,则对任意 都满足 Hall 条件(因为 来自两侧,邻居落在不同的两侧,不会重叠),从而存在匹配覆盖。
那么只需要状压点集合即可,分别状压,将合法方案存储下来,最后统计答案的时候用二分求出有多少个合法点即可,时间复杂度。
总结:二分图的独立性(只需要考虑某一部的具体情况)
[AGC032E] Modulo Pairing
将 分为 和。如果我们只有单独一类的话我们显然可以通过将 排序后贪心即可,然而问题在于这是一个混合在一起的。
我们考虑能否融合这些贪心方法,那么必然存在一个分界点,使得 左边第一种贪心, 右边用第二种贪心。下图的蓝线表示一类匹配,红线表示二类匹配:
证明可以考虑调整法:
左边一列的调整是平凡的,右边一类的调整可以考虑:蓝色匹配的代价必然 ≥ 右端点,红色匹配的代价必然 < 左端点,那么不难发现调整之后最大代价都是变小了的。
但是分界点怎么求呢,根据调整的过程,我们可以考虑二分求出分界点,时间复杂度。
总结:
混合多种方法的思路十分重要,例如根号分治。对于贪心问题,混合贪心可以让局部最优,我们再考虑怎么从局部最优拓展到整体最优即可;
CF1131G Most Dangerous Shark
想起来一些不好的回忆,想起来 ARC 的某个题了呜呜呜呜呜。
首先,不难发现倒下骨牌的过程中,其骨牌高度 单调不降。也就是说我们可以通过单调栈来预处理每个骨牌所能向左向右倒影响的最远位置 和,具体如何计算见代码。
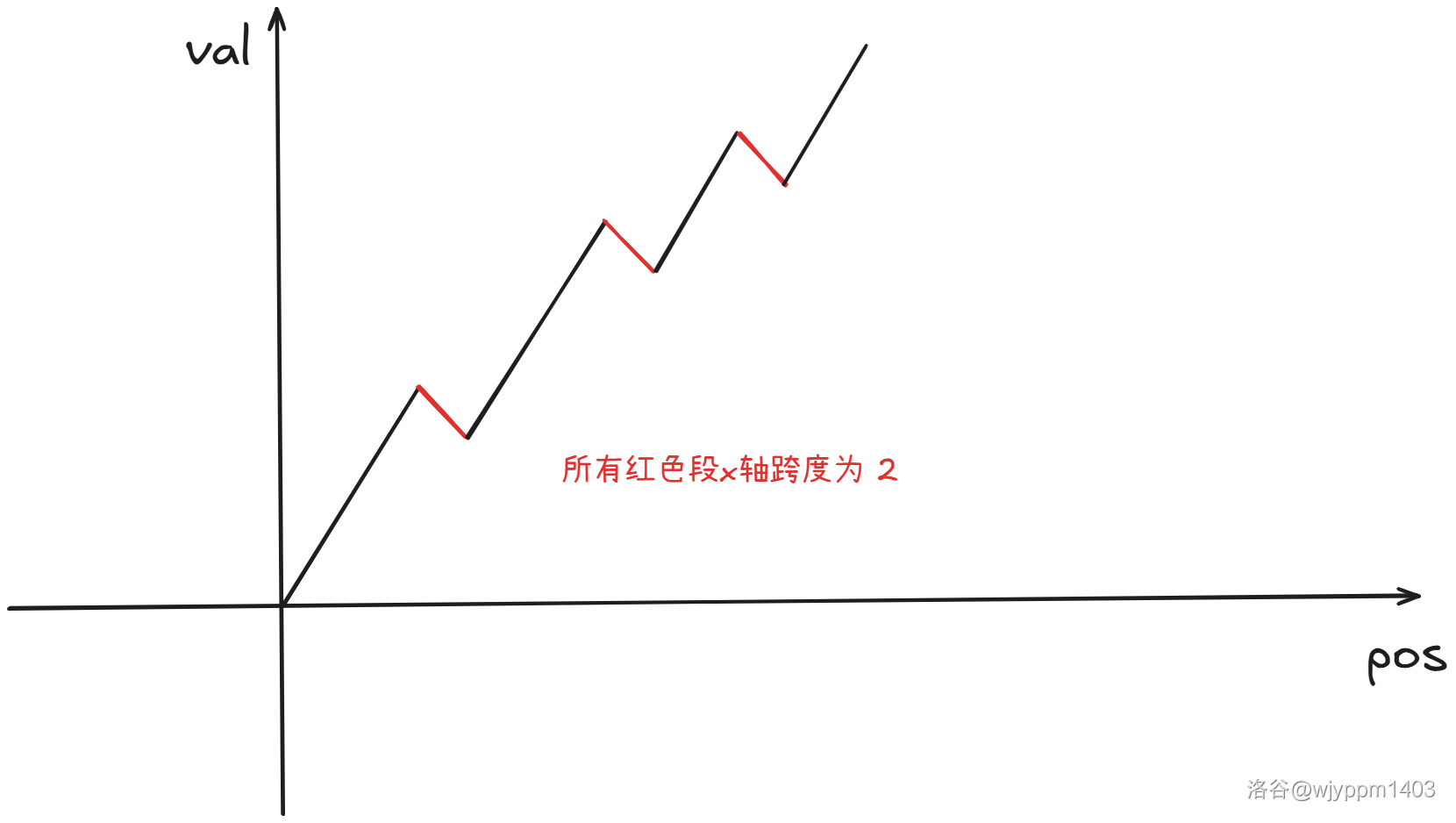
这样你就得到了一些区间,现在问题转化为要求选取一些区间使得能够覆盖所有点(覆盖的点不能再选)。考虑 DP,根据 CF1476F 灯塔题不难想到设 表示前 骨牌被推倒的最小代价,转移:
第一种根据贪心显然只需要考虑 的转移就可以了,第二个可以通过线段树优化,时间复杂度 无法通过,考虑优化,但是发现这玩意不太好搞因为是一个区间查询。
考虑进一步对区间发掘性质,我们根据上面骨牌高度 单调不降,那么同时也能不难发现区间范围也是单调不降的,进一步推论:每个骨牌的覆盖范围要么包含,要么相离。考虑单调栈优化 DP,每次新加入的点就放在栈顶,每次只需要考虑栈顶得覆盖范围够不够,不够直接弹出,然后维护一个栈的前缀最小值就可以转移了。时间复杂度。
总结:对于数列覆盖问题,常有的结论是两个点的覆盖范围要么包含、要么相离,这时候可以选择用单调数据结构维护(因为覆盖范围单调),而不是带 log 的数据结构。
P2305 [NOI2014] 购票
首先有一个及其显然的 DP,设 表示 点向上跳祖先的最小花费,有转移:
直接做,时间复杂度。考虑转化 DP 形式,不难有:
不难发现后面是一次函数,在没有转移限制情况下用李超线段树维护即可,但是问题在于有了限制怎么办。发现考虑上距离的限制其实就是多加了一维偏序关系,所以我们可以用树套树。一种空间消耗较小的树套树方法是,我们预处理出每个点的欧拉出序,外层线段树以欧拉出序来建立。询问时先二分出可以到达的最浅祖先,然后可以得到一个欧拉出序的区间,这个区间只包含这个点到祖先的路径,因为还没访问到的点没被加入到李超树中,那么插入的时候不用回撤,直接插入即可。时间复杂度。
总结:发现题目有不可解决的维度时,要敢于使用数据结构。但是此时空间消耗特别重要,注意处理 dp 的顺序,才能时数据结构的使用简单化,并且减少常数的消耗。
这里出栈序的应用也十分经典,引用了欧拉出序的区间,区间只包含这个点到祖先的路径这个优美的性质来防止李超树的回退,将一段具有祖孙关系的点对之间的路径直接映射到了序列上的一段区间从而将树上问题转化成了序列上的问题。
CF303E Random Ranking
除了序列大小转 01 之外序列我是真不知道还能这么玩!
对区间离散化,然后呢?
首先考虑一个简单的问题,如果所有人选取的值域区间一致,那么一个人获得 的排名概率都是。
那么我们考虑对于离散化后端点所构成的每一个小段,我们把一些人分配到小段的左边,把一些人分配到小段的右边,并钦定某个值在里面。然后来统计答案:
设 表示 个数所在区间比它小, 个数所在区间比它大,剩下的人都在小段中的概率。一个人的概率可以通过讨论线段关系简单计算,那么这就变成一个背包问题了。时间复杂度是 的。统计答案时枚举 ,对于这,可能的排名为 ,这些排名一定是等概率的,因为区间 内的这些值是全是随机的, 在每个排名的概率是相同的,精髓就是我们通过合理的状态设计将复杂问题划归为简单的问题。直接做是。可以用 CDQ 分治优化,时间复杂度。
总结:
很多实数概率题的技巧通常是,先解决一个能用概率简单计算的子问题,然后把原问题化归到这个简单问题上,想本题所使用的划归思想。
种不太好记录之前的值的信息,不好考虑完整的大小关系的随机问题一种套路做法是考虑枚举一个值,作为最终取的值或是前几大的分界线考虑,再来统计其他值和这个值的相对大小关系。
AT_abc219_h
没法记录时间,这不是矩阵快速幂,不知道蜡烛具体长度,是我们知道每一秒蜡烛会减少 1 的长度,所以应用费用提前计算的思想,我们可以计算有多少个以后吹熄的蜡烛受到了这次减少的影响。
发现走的过程必定是一个区间,要么拓展当前位置一步,要么走到另一头。考虑区间 DP,设 表示 区间,在 还是 的方案,转移考虑向左向右或者从一端走到一端决策即可。但是我们没有办法算代价,因为蜡烛可能燃烧完毕,我们发现,相当于选择一些蜡烛不去选择,最优情况下一定是都选择会产生正贡献的蜡烛,错解不优。
所以加一维度 表示还有 个需要选择,答案就是,时间复杂度。
总结:如果当前状态不好知道,但你清楚代价的变化规则时,可以费用提前计算。
P6847 [CEOI 2019] Magic Tree
今天没有什么太好的性质,考虑 DP,设 表示 子树内断边在 的时间断开,转移:
- 不获取 u 点的果汁:
- 断开父边,获取 u 点的果汁:,其中。
线段树合并来优化,第一种转移就直接线段树合并,第二种转移不能维护区间最值标记。而且合并不太好维护,考虑分析性质,发现 随 增加而单调,那么第二种转移可以考虑成区间赋值。实现中区间赋值不打标记,而是线段树上的点维护 min,max,如果 min=max 的时候就说明这个区间是一个值,线段树合并的时候如果遇到区间同值的情况就打加法标记,修改的时候如果区间同值就新开儿子节点,上传的时候如果发现区间同值可以把儿子节点删掉,时间复杂度。
更 nb 的,因为 dp 值单调所以可以考虑差分,那么第一种转移就能直接启发式合并,第二种转移是增加 的差分值,直接插入 set 中,这其实是取 max 操作,所以要从后面删除一些差分标记,时间复杂度。
[ARC120F] Wine Thief
可怜的 PPM 从暑假到做这个题之前都不知道学长口中所说的环上每个位置是等价的到底指的是是什么?做完这个题后 PPM 直接星宇大发!
上来直接拆贡献,然后问题在于你不会算合法的方案数,对于每个位置的方案数几乎是本质不同的。如果直接去算的话你还需要枚举选择大小时间复杂度是 的没法搞(其实可以)。
先考虑简单一点的,如果没有 的限制,就是单纯的让你链上选择独立集,根据插板法不难得出答案即为。现在我们考虑如何处理每个位置的方案数,由于我们不可能枚举选了多少个不然复杂度还是 的,考虑到如果我们不去枚举那么这个序列要求我们枚举的位置必须等价,考虑链上的位置是不等价,但是环上的位置是等价的。所以考虑转为环,此时方案数为,如果位置在 和 的时候就是。是此时 都选的方案是没有算上的。不过我们发现当钦定 1,n 都选时我们进入了一个子问题,子问题仍然可以放在一起处理,也就是说方案数是以一种 的形式出现,前缀和维护即可,时间复杂度。
CF1528F AmShZ Farm
哦我的天啊这简直简直了。
两个限制,我们先单独讨论一个限制如何满足,比如说 的限制。我们发现限制可以如下转化:有 个凳子, 个人手里拿着一个位置编号排队就座。第 个人如果当前位置没有人坐就坐,如果有人就往后找到第一个没有人的凳子坐下来,合法当且仅当每个人都能找到座位。这个性质也很好,但是问题如何快速判断每个人能否找到座位?我们可以在最后一个位置加一个哨兵座位,如果排完座位后 没人的话那么就是合法的。
但是 相等限制怎么处理,上面这个操作很不方便我们进行计数,原因就是在于我们选位置每个节点都只能向右选,位置是不等价的,不方便我们进行计数。我们发现如果我们将首尾相接,形成一个环,环上位置就是等价的就方便我们计数。
考虑进一步发掘点有用的,我们发现 的组合意义其实就是就是一个 的贡献是其中每种数数量的 次方的和。同时发现这个环如果我们钦定一个点为,断环为链,而 中合法元素因为只要出现次数满足可以分配,即设 表示 数出现次数,满足 的话就可以了。所以 都是循环同构的,而这些组中 的贡献都是一致的。我们可以对所有的 进行计算后除掉 即为答案。
现在考虑每个元素的贡献,答案需要乘上 发现消掉了,太好了,那么直接通过 来卡 的限制,枚举该元素出现次数,那么答案为:
由于 较小,考虑斯特林反演有:
注意到:,有:
可以二项式反演,答案即为:
用第二类斯特林数·行的技巧算一下就可以啦,时间复杂度。
总结:等概率环是一个很重要的玩意,链上的位置是不等价的,但是环上是等价的,所以我们可以考虑。
CF512D Fox And Travelling
首先可以将标记看作删除,其次根据题目限制不难发现合法的删除操作必定每次删除的点度数都。然后我们发现满足这个性质的只有树,环是没有用的,说严谨点将原图去掉环后合法的都是森林。
那先考虑树怎么做,显然飞上去一个树形 DP 设 表示 子树内选了 个点的方案数,转移枚举合并上来,还要乘上一个 的组合数,时间复杂度。
注意到我在玩文字游戏,上面只是说树了没说是有根树还是无根树,显然无根树有一堆重复方案,我们考虑这些重复方案有什么性质,发现无根树定根时做 DP 每种选择 个点的方案会被多算 次,其中 为这棵无根树的大小,那么除掉即可,时间复杂度。
CF914F Substrings in a String
bitset 好神秘!
对 26 个字母各开一个 bitset,存这个字母出现的位置。
对于询问,新建一个 bitset。从前到后枚举询问串的每个位置 yi,和这个字母对应的 bitset 右移 i 位取 and。
最终得到的 bitset 中 1 的个数即为询问串在原串出现次数。
P5355 [Ynoi Easy Round 2017] 由乃的玉米田
bitset 神秘密!
首先飞一个莫队上去,考虑加法操作如何解决,显然只要存在 即可满足,而题目只要求可行性而非要求个数,故考虑 bitset 维护值域数是否出现,那么加法操作就是 (s1&(s1<<qry[i].x)).any(),其中 表示值域维护。
然后考虑减法,显然减法可以维护一个 的 bitset,设为,那么判断方法就是:(s1&(s2>>(1e5-qry[i].x))).any()。然后考虑乘法,枚举约数 做。问题在于除法很难维护,考虑根号分治, 的暴力找。但是问题在于 怎么做?
先将询问按左端点降序排列。然后取一个指针,一开始指向 。若当前询问的左端点为 ,则将 上所有元素的贡献插入树状数组中,并使 ,完成后直接在树状数组上获取当前询问的答案,时间复杂度,直接做即可。
P4465 [国家集训队] JZPSTR
bitset,bitset,bitset!
虽然标程是分块加 SAM, 但是显然大家都不喜欢这么毒瘤的。注意到插入删除询问次数独立的都很少,并且字符集很少,考虑 bitset。我们维护每个字符在哪些位置上出现过,记 字符出现在 集合的位置,现有匹配串,维护当前仍然合法的起始点集合,则有。
讲完了就好说了,强两个操作显然可以用位运算暴力,第二个就用我们上面的操作,时间复杂度是 其中。
轻松最优解第二位,不知道第一位如何做到?