0.前情提要

在学长的课上听到了颜色段覆盖问题,顺手讲了个ODT,当时的我以为就是一个可爱的数据结构,但是学下来发现确实很可爱(。・ω・。)
CF896C——ODT的起源


你需要知道——STL的set怎么用(cppreference)
对就这些。
1.什么是珂朵莉树
珂朵莉树,又称ODT(老司机树),是一种利用set的暴力数据结构,用于解决区间问题的数据结构。
2.珂朵莉树可以解决什么问题
区间推平问题出现的时候我们就可以用珂朵莉树了。她高效的基础是当数据随机生成的时候,复杂度是正确的(见下文),但是若没说,你就要开赌,这个很容易被构造数据卡掉。
3.珂朵莉树的构造
借用一下大佬的图

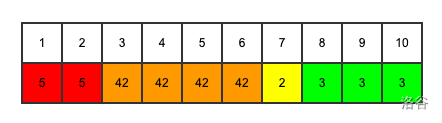
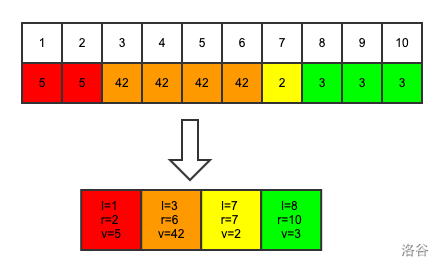
对于珂朵莉树的节点,我们维护的是一个数值相同的区间,如上图。我们考虑维护一个三元组(l,r,val),其中l和r是数值相同区间的左右端点,val就是这个区间对应的数值,那么每个相同数列的区间就可以浓缩为一个节点,如下图

当然在维护区间的时候我们要满足区间左端点和右端点都样单调递增,这里只需要比较左端点就可以了。
代码如下
当然对于CF896C我们一开始维护n个长度为1的单点
1
2
3
4
5
6
7
8
9
10
11
12
13
| struct kdltree
{
int l,r;
mutable ll val;
kdltree(int L,int R=-1,ll V=0){
l=L,r=R,val=V;
}
bool operator<(const kdltree&a)const{
return l<a.l;
}
};
set<kdltree> odt;
|
4.split分裂区间
如果我们想要的修改范围对于一个大区间来说小的话,我们就需要把区间拆开成我们想要的
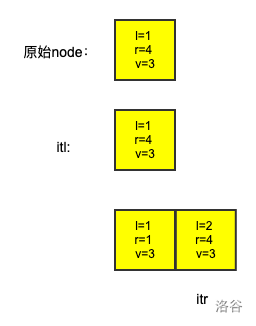
split就是干这个的,他的唯一一个需要的参数就是pos,代表意义就是把一个[L,R]的区间劈成[L,pos−1],[pos,R]
很显然利用set的平衡树特性,我们可以用lower_bound函数找到其对应的区间节点
接下来分类讨论,其实也挺简单的
- 如果pos刚好是区间节点的左端点(就是找到pos的具体数值了),那么分裂都不用分,直接返回即可
- 如果不是,那么因为lower_bound是≥的操作,那么这里返回的是pos右边对应的区间节点,那么我们只需要将获取到的迭代器it–就可以获得其对应的节点,让后一刀劈成[L,pos−1],[pos,R]
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
|
auto split(int pos){
auto it=odt.lower_bound(kdltree(pos));
if(it!=odt.end()&&it->l==pos){
return it;
}
it--;
int l=it->l,r=it->r;
ll val=it->val;
odt.erase(it);
odt.insert(kdltree(l,pos-1,val));
return odt.insert(kdltree(pos,r,val)).first;
}
|
5.区间推平
其实在构造区间节点的时候我们发现,这个数据结构其实就是天生适合区间推平这个操作的,因为她刚好存储的就是一个区间相同的值的。

例如我们将[2,8]这个区间推平改为666,set里面有4个区间节点。首先我们发现[8,10]是一个区间,那么要先split(8+1),拆成[8,8]和[9,10]两个区间。同理,[1,2]这个区间我们要拆成[1,1]和[2,2]
1
2
3
4
5
6
7
8
9
10
|
void merge(int l,int r,ll val){
auto itr=split(r+1);
auto itl=split(l);
odt.erase(itl,itr);
odt.insert(kdltree(l,r,val));
}
|
注意这里不能先分左再分右!

先分左再分右,你会发现这个itr和itl指向的东西出事了,如果你erase就会出问题,直接RE
但是问题在于这个顺序反了也有可能会AC,这个RE的概率是大约1%,随机RE。十分的“珂”学。最好还是先右再左
6.更新查询操作
对于任意的更新查询操作我们可以套如下的模板
- 先split右,在split左把区间[l,r]搞出来
- 暴力,启动!
这里我们贴上CF896C的几个操作,体会一下模板的套用(゚∀。)
- 区间加
1
2
3
4
5
6
7
| void add(int l,int r,ll val){
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
it->val+=val;
}
}
|
2.区间第k小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| typedef pair<ll,int> kdl;
ll topk(int l,int r,int k){
vector<kdl> a;
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
a.push_back(kdl(it->val,it->r-it->l+1));
}
sort(a.begin(),a.end());
for(auto it=a.begin();it!=a.end();it++){
k-=it->second;
if(k<=0){
return it->first;
}
}
return -1;
}
|
- 区间幂次和(这里使用的是快速幂)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| ll fastpow(ll x,ll y,ll mod){
ll res=1;
x%=mod;
while (y>0)
{
if(y&1){
res=res*x%mod;
}
x=x*x%mod;
y>>=1;
}
return res;
}
ll sum(int l,int r,int x,int y){
ll ans=0;
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
ans=(ans+fastpow(it->val,x,y)*(it->r-it->l+1))%y;
}
|
7.时间复杂度
这里前提条件是数据随机情况下复杂度正确,如果数据不随机会出现O(nm)的错误时间复杂度
一般来说仅区间推平这一个区间操作的时间复杂度是均摊O(log2log2n),如果有暴力操作就是O(log2n),我们发现这个数据结构能够高效的关键在于区间推平,区间推平能把小区间合并成一个大区间,这是珂朵莉树高效的关键,也是她适用范围小的原因。
很容易被构造数据卡掉,导致变成一个一个散点。
8.代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
| #include<iostream>
#include<set>
#include<algorithm>
#include<vector>
#define ll long long
using namespace std;
const int MOD=1000000007,MN=1e5+15;
ll n,m,seed,vmax;
ll a[MN];
ll rnd(){
ll ret=seed;
seed=(seed*7+13)%MOD;
return ret;
}
struct kdltree
{
int l,r;
mutable ll val;
kdltree(int L,int R=-1,ll V=0){
l=L,r=R,val=V;
}
bool operator<(const kdltree&a)const{
return l<a.l;
}
};
set<kdltree> odt;
auto split(int pos){
auto it=odt.lower_bound(kdltree(pos));
if(it!=odt.end()&&it->l==pos){
return it;
}
it--;
int l=it->l,r=it->r;
ll val=it->val;
odt.erase(it);
odt.insert(kdltree(l,pos-1,val));
return odt.insert(kdltree(pos,r,val)).first;
}
void merge(int l,int r,ll val){
auto itr=split(r+1);
auto itl=split(l);
odt.erase(itl,itr);
odt.insert(kdltree(l,r,val));
}
void add(int l,int r,ll val){
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
it->val+=val;
}
}
typedef pair<ll,int> kdl;
ll topk(int l,int r,int k){
vector<kdl> a;
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
a.push_back(kdl(it->val,it->r-it->l+1));
}
sort(a.begin(),a.end());
for(auto it=a.begin();it!=a.end();it++){
k-=it->second;
if(k<=0){
return it->first;
}
}
return -1;
}
ll fastpow(ll x,ll y,ll mod){
ll res=1;
x%=mod;
while (y>0)
{
if(y&1){
res=res*x%mod;
}
x=x*x%mod;
y>>=1;
}
return res;
}
ll sum(int l,int r,int x,int y){
ll ans=0;
auto itr=split(r+1);
auto itl=split(l);
for(auto it=itl;it!=itr;it++){
ans=(ans+fastpow(it->val,x,y)*(it->r-it->l+1))%y;
}
return ans;
}
int main(){
cin>>n>>m>>seed>>vmax;
for(int i=1;i<=n;i++){
a[i]=rnd()%vmax+1;
odt.insert(kdltree(i,i,a[i]));
}
for(int i=1;i<=m;i++){
int op=rnd()%4+1,l=rnd()%n+1,r=rnd()%n+1,x,y;
if(l>r) swap(l,r);
if(op==3){
x=rnd()%(r-l+1)+1;
}else x=rnd()%vmax+1;
if(op==4) y=rnd()%vmax+1;
if(op==1){
add(l,r,x);
}else if(op==2){
merge(l,r,x);
}else if(op==3){
cout<<topk(l,r,x)<<endl;
}else cout<<sum(l,r,x,y)<<endl;
}
return 0;
}
|
10.拓展
ODT映射思想的推广