0. 前言

你需要知道树状数组

1. 树状数组二分

1.1 概念

类似于线段树二分，树状数组当然也可以二分。

它解决的是如下一类问题：

对于序列aa，存在分割点qq 使得≤q\le q 的位置满足某个限制而>q>q 的位置不满足限制，求qq。
（注意是整个序列aa 找分割点），要求O(nlog⁡n)O(n\log n)。
nn 类似于长度。

如果你是从某个位置开始二分，那这个就做不到，你可以考虑转化到整个序列二分。

考虑最后一个前缀和≤v\le v 的位置，满足序列每个元素非负，则存在分割点qq 满足≤q\le q 的位置的前缀和≤v\le v ，而>q>q 的位置的前缀和>v>v ，那么qq 即为所求。

我们初始化两个变量，当前位置pp 和对应的前缀和ss，初始权为 0。

我们从大到小枚举1≤2k≤n1\le 2^k \le n，尝试将pp 加上2k2^k。检查s+∑i=p+1p+2kai≤vs+\sum\limits_{i=p+1}^{p+2^k} a_{i}\le v 是否成立，因为kk 从小到大枚举，此时lowbit(p)>2klowbit(p)>2^k，那么显然有lowbit(p+2k)=2klowbit(p+2^k)=2^k，因为树状数组中t[i]t[i] 中填的是[i−lowbit(i)+1,i][i-lowbit(i)+1,i] 这个区间的信息，那么也就是说t[p+2k]=∑i=p+1p+2kait[p+2^k]=\sum\limits_{i=p+1}^{p+2^k} a_{i}。

那么就可以这么做：

  • 初始化两个变量，当前位置pp 和对应的前缀和ss，初始权为 0。
  • 从大到小枚举1≤2k≤n1\le 2^k \le n。
    • 若p+2k≤np+2^k\le n 且s+t[p+2k]≤vs+t[p+2^k]\le v。则p←p+2k,s←s+t[p+2k]p\leftarrow p+2^k,s\leftarrow s+t[p+2^k]。
    • 若p+2k>np+2^k>n，啥也不做。

pp 一定等于最终求的qq，否则pp 在过程一定会变得更大。

1.2 例题

[省选联考 2020 A/B 卷] 冰火战士

经典畅谈。

一个显然能看出来，我们要二分温度kk。

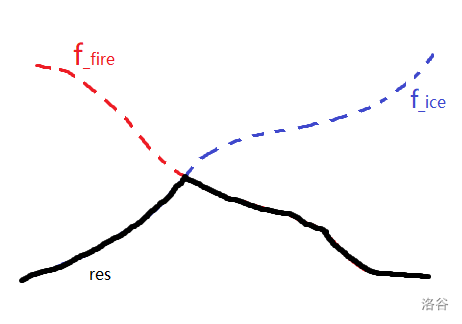
首先考虑能不能三分，显然不行这个是离散的，但是对于冰的能量求和ficef_{ice} 是单调不降的，而ffiref_{fire} 是单调不升的。如果画出来的话就是两个函数打叉，我们就是要找那个叉。

借用 duyi大佬的图：

我们要找的就是这个叉，但是这个叉直接二分求有点难找。

我们可以两次二分，第一次找最大的kk 使得fice(k)<ffire(k)f_{ice}(k) < f_{fire}(k)，以此为左边界，第二次找最小的kk 使得fice(k)≥ffire(k)f_{ice}(k)\ge f_{fire}(k) 。

不难发现可以离线询问，我们考虑怎么维护这个区间修改ff ，其实也很简单，差分就可以了。但是这里面有一个后缀和耶？那怎么办？其实后缀和就是总和-前缀和，让后做完了。

对于倍增查询，时间复杂度因为查询的是树状数组的数据，可以做到O(log⁡q)O(\log q) ，所以总时间复杂度为O(qlog⁡q)O(q \log q)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MQ=2e6+15;
int q,a[MQ],tot,sum1;

struct query{
    int op,t,x,y;
}qry[MQ];

struct BIT
{
    private:
        int t[MQ];
    public:

    inline int lowbit(int x){
        return x&-x;
    }

    void update(int pos,int k){
        while(pos<MQ){
            t[pos]+=k;
            pos+=lowbit(pos);
        }
    }

    int query(int x){
        int ret=0;
        while(x){
            ret+=t[x];
            x-=lowbit(x);
        }
        return ret;
    }

    int get(int x){
        return t[x];
    }
}t0,t1;

template<typename type>
void read(type &x){
    x=0;bool flag(0);char ch=getchar();
    while(!isdigit(ch)) flag=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    flag?x=-x:0;
}

void lisan(){
    sort(a+1,a+1+tot);
    tot=unique(a+1,a+1+tot)-a-1;
    for(int i=1;i<=q;i++){
        if(qry[i].op==2) continue;
        qry[i].x=lower_bound(a+1,a+1+tot,qry[i].x)-a;
    }
}

signed main(){
    read(q);
    for(int i=1;i<=q;i++){
        read(qry[i].op);
        if(qry[i].op==1){
            // cin>>qry[i].t>>qry[i].x>>qry[i].y;
            read(qry[i].t);
            read(qry[i].x);
            read(qry[i].y);
            a[++tot]=qry[i].x;
        }else read(qry[i].t);
    }
    lisan();
    for(int i=1;i<=q;i++){
        if(qry[i].op==1){
            if(qry[i].t){
                t1.update(qry[i].x+1,qry[i].y);
                sum1+=qry[i].y;
            }else t0.update(qry[i].x,qry[i].y);
        }else{
            int p=qry[i].t;
            if(qry[p].t){
                t1.update(qry[p].x+1,-qry[p].y);
                sum1-=qry[p].y;
            }else t0.update(qry[p].x,-qry[p].y);
        }
        int s0=0,s1=sum1,f0=0,f1=0,p0=0,p1=0;
        for(int j=20;j>=0;j--){
            int np=p0+(1<<j),ns0=s0+t0.get(np),ns1=s1-t1.get(np);
            if(np>tot) continue;
            if(ns0<ns1){
                p0=np;
                s0=ns0,s1=ns1;
            }
        }
        f0=s0,s0=0,s1=sum1;
        if(p0<tot){
            f1=min(t0.query(p0+1),sum1-t1.query(p0+1));
            for(int j=20;j>=0;j--){
                int np=p1+(1<<j),ns0=s0+t0.get(np),ns1=s1-t1.get(np);
                if(np>tot) continue;
                if(ns0<ns1){
                    p1=np;
                    s0=ns0,s1=ns1;
                }else if(min(ns0,ns1)==f1){
                    p1=np;
                    s0=ns0,s1=ns1;
                }
            }
        }
        if(max(f0,f1)==0) cout<<"Peace\n";
        else if(f0>f1) cout<<a[p0]<<" "<<f0*2<<'\n';// 最小的能量消耗一定消耗完了，并且两边消耗同样做小
        else cout<<a[p1]<<" "<<f1*2<<'\n';
    }
    return 0;
}

[USACO03Open] Lost Cows

虽然原题是O(n2)O(n^2) 就能做，但是这里我们强制要求O(nlog⁡n)O(n\log n)。

但是我们先从暴力开始做，首先观察到如果正着做太难了而且后效性太大了受不了。正难则反，考虑倒着走，发现倒着走很好做啊，因为原题中的aia_i 看得是前面而不是后面，这样我们就可以利用后面占用的信息往前推过去了。

一个显然O(n2)O(n^2) 的做法就是考虑怎么分配编号，直接开visvis 数组记录编号谁占了，其实就是找在visvis 数组前缀和为ai+1a_{i}+1 的位置（随便找就行），找到后标 1 即可。

我们考虑怎么优化，上述瓶颈的过程在于查询前缀和，观察数组的性质，不难发现是一个 01 序列， 那么对于前缀和的形式我们可以直接转化成查询第ai+1a_{i}+1 个的 1 的位置，让后单点修改为 1 即可。

综上，我们要造一个数据结构，满足能够支持查询第kk 个 1 的位置（k∈N+k\in \mathbb{N}^+），并且支持单调修改，时间复杂度要求操作都为log⁡n\log n 的时间复杂度。

不难发现它找的就是：满足在≤pos\le pos 的位置vv 的前缀和≤k\le k，而在>pos>pos 的位置vv 的前缀和>k>k，找的就是这个分界点。

这里我们可以用 树状数组+真正的二分 来做，其实也很简单，直接考虑二分答案，用查询函数queryquery 查询里面的数据就能获得前midmid 有多少个 1 ，让后直接比较大小二分即可，但是这样的时间复杂度是O(nlog⁡2n)O(n\log ^2 n)。

考虑用我们讲的方法，直接做，时间复杂度分析和上面题一样为O(nlog⁡n)O(n \log n)，其实到这里你应该能发现树状数组恰好为我们维护了区间长度为22 的次幂的一些信息，所以我们不需要二分，直接利用树状数组这个特性倍增就能完成和真正二分一样的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
constexpr int MN=1e6+15;
int n,a[MN],ans[MN];
struct BIT{
    int t[MN];

    int lowbit(int x){
        return x&-x;
    }

    void update(int x,int k){
        while(x<MN){
            t[x]+=k;
            x+=lowbit(x);
        }
    }

    int query(int x){
        int ret=0;
        while(x){
            ret+=t[x];
            x-=lowbit(x);
        }
        return ret;
    }

}bit;

int main(){
    cin>>n;
    bit.update(1,1);
    for(int i=2;i<=n;i++){
        cin>>a[i];
        bit.update(i,1);
    }
    for(int i=n;i>=1;i--){
        int p=0,s=0;
        for(int j=20;j>=0;j--){
            int np=p+(1<<j);
            if(np>n) continue;
            int ns=s+bit.t[np];
            if(ns<a[i]+1){
                s=ns;
                p=np;
            }
        }
        p++;
        bit.update(p,-1);
        ans[i]=p;
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<'\n';
    return 0;
}

[POI 2015] LOG

维护一个长度为nn 的序列，一开始都是00，支持以下两种操作：

  1. U k a 将序列中第kk 个数修改为aa。
  2. Z c s 在这个序列上，每次选出cc 个正整数，并将它们都减去11，询问能否进行ss 次操作。
    询问独立。
    时间复杂度要求O(nlog⁡n)O(n\log n)，都是正整数不是正数。
    but：1≤n≤106,1≤k,c≤n,1≤a,s≤1091\le n \le 10^6,1\le k,c\le n,1 \le a,s \le 10^9。

可以先自己想想。
这里的ss 次操作选出的正数可以不同。

提示：贪心复杂度走不了思考一下排序是为了什么。

一个贪心的思路就是每次排序，找最大的那几个往后数，这个显然是正确的，但是这样的时间复杂度是O(n2log⁡n)O(n^2 \log n)，不能通过。

虽然贪心过不去，但是我们可以借鉴贪心中排序，我们排序是为了什么，其实就是为了发掘性质。实际上，我们不难发现每一次排序中总有数会被选择，那么就是那些≥s\ge s 的数一定会被选择（长的高天塌下来先砸到他们www），一旦他们能够承受ss 次操作的话那么万事大吉，如果一旦都 GG 了就得让<s<s 的承受了，我们考虑这个承受能否，如何判断？其实也很简单，如果每个数最终都减到 0 了还是不够那就完蛋，如果没有那就还是可以的。所以我们需要<s<s 的数的和sumsum，判断一下就可以了。

等一下，到底怎么判断？

实际上，我们假设一个极端情况，就是那些大于等于ss 的数都等于ss，在这个极端情况下，必须保证sum≥(c−x)×ssum\ge (c-x)\times s，其中xx 为≥s\ge s 的数的个数，只有这样才能保证可以，如果不是极端情况，那么最少也有⌈sums−1⌉\lceil \dfrac{sum}{s-1} \rceil 个数，如果满足sum≥(c−x)×ssum\ge (c-x)\times s，那么满足⌈sums−1⌉>c−x\lceil \dfrac{sum}{s-1} \rceil > c-x，这个时候肯定有解的。

有如下做法：

  1. 在线做法，平衡树或动态开点值域线段树瞎做，时间复杂度显然O(nlog⁡n)O(n\log n)。
  2. 离线下来，值域树状数组做，时间复杂度在离散化后也为O(nlog⁡n)O(n \log n)。这个做法是最简单的。
  3. 离线离散化，树状数组二分找这个≥s\ge s 的数的个数，其实个上面第二个例题差不太多，只不过是倒着找，但是本质不如第二个做法简单。时间复杂度仍为O(nlog⁡n)O(n \log n)。

第二种我写的，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=1e6+15;
struct query{
    int op,k,a,c,s;
}q[MN];
int n,m,tot,ls[MN],a[MN];

struct BIT{
    private:
        int t[MN];

    public:

    inline int lowbit(int x){
        return x&-x;
    }

    int query(int x){
        int ret=0;
        while(x){
            ret+=t[x];
            x-=lowbit(x);
        }
        return ret;
    }

    void update(int x,int k){
        while(x<MN){
            t[x]+=k;
            x+=lowbit(x);
        }
    }

    int get(int x){
        return t[x];
    }

}b1,b2;

void lisan(){
    sort(ls+1,ls+1+tot);
    tot=unique(ls+1,ls+1+tot)-ls-1;
    for(int i=1;i<=m;i++){
        if(q[i].op){
            q[i].s=lower_bound(ls+1,ls+1+tot,q[i].s)-ls;
        }else q[i].a=lower_bound(ls+1,ls+1+tot,q[i].a)-ls;
    }
}

signed main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        char op;
        int x,y;
        cin>>op;
        if(op=='U'){
            q[i].op=0;
            cin>>q[i].k>>q[i].a;
            ls[++tot]=q[i].a;
        }else{
            q[i].op=1;
            cin>>q[i].c>>q[i].s;
            ls[++tot]=q[i].s;
        }
    }
    lisan();
    for(int i=1;i<=m;i++){
        if(q[i].op==0){
            int x=0;
            if(x=a[q[i].k]){
                b1.update(x,-1);
                b2.update(x,-ls[x]);
            }
            x=a[q[i].k]=q[i].a;
            b1.update(x,1);
            b2.update(x,ls[q[i].a]);
        }else{
            int x=b1.query(tot)-b1.query(q[i].s-1);
            int sum=q[i].s?b2.query(q[i].s-1):0;
            if(sum>=(q[i].c-x)*ls[q[i].s]){
                cout<<"TAK\n";
            }else cout<<"NIE\n";
        }
    }
    return 0;
}

普通平衡树

洒洒水啦，复杂度依旧是O(qlog⁡n)O(q\log n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <bits/stdc++.h>
using namespace std;
constexpr int MN = 1e5 + 15;
int n, m, tot, op[MN], a[MN], b[MN];
struct BIT
{
    int t[MN];

    int lowbit(int x)
    {
        return x & -x;
    }

    void update(int x, int k)
    {
        while (x < MN)
        {
            t[x] += k;
            x += lowbit(x);
        }
    }

    int query(int x)
    {
        int ret = 0;
        while (x)
        {
            ret += t[x];
            x -= lowbit(x);
        }
        return ret;
    }

    int getkth(int x)
    {
        int p = 0, s = 0;
        for (int i = 20; i >= 0; i--)
        {
            int np=p+(1<<i);
            if(np>tot) continue;
            int ns=s+t[np];
            if(ns<x){
                s=ns;
                p=np;
            }
        }
        return p+1;
    }

} bit;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> op[i] >> a[i];
        b[i] = a[i];
    }
    sort(b + 1, b + 1 + n);
    tot = unique(b + 1, b + 1 + n) - b - 1;
    for (int i = 1; i <= n; i++)
    {
        if (op[i] == 4)
            continue;
        a[i] = lower_bound(b + 1, b + 1 + tot, a[i]) - b;
    }
    for (int i = 1; i <= n; i++)
    {
        if (op[i] == 1)
        {
            bit.update(a[i], 1);
        }
        if (op[i] == 2)
        {
            bit.update(a[i], -1);
        }
        if (op[i] == 3)
        {
            cout << bit.query(a[i] - 1)+1<< '\n';
        }
        if (op[i] == 4)
        {
            cout<<b[bit.getkth(a[i])]<<'\n';
        }
        if(op[i]==5){
            cout<<b[bit.getkth(bit.query(a[i]-1))]<<'\n';
        }
        if(op[i]==6){
            cout<<b[bit.getkth(bit.query(a[i])+1)]<<'\n';
        }
    }
    return 0;
}

2. 维护矩形

对于普通 BIT 来说，满足的就是一维度（其实就是数组）的区间查询与单点修改。

对于二维 BIT 来说，它可以做到单点加矩形查询，只需要差分就能做到对任意矩形求和，对于查询修改时间复杂度都是优秀的O(log⁡2n)O(\log^2 n)。

但是我们给它上上难度呢？

P4514 上帝造题的七分钟

给定矩阵大小为n×mn\times m，你需要写一个O(qlog⁡nlog⁡m)O(q\log n \log m)（其中qq 为询问个数)，的数据结构维护如下操作
L a b c d k —— 代表将(a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内的所有数字加上kk。
k a b c d —— 代表求(a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内所有数字的和。

矩形加矩形求和，就是维护二维差分数据的二阶二维前缀和，考虑(i,j)(i,j) 的差分修改对(x,y)(x,y) 查询的贡献，不难发现总共加了(x−i+1)(y−j+1)k(x-i+1)(y-j+1)k 个数。展开有(x+1)(y+1)k−(y+1)ik−(x+1)jk+ijk(x+1)(y+1)k-(y+1)ik-(x+1)jk+ijk，维护k,ik,jk,ijkk,ik,jk,ijk 的二维前缀和即可。

故代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=1e6+15;
struct query{
    int op,k,a,c,s;
}q[MN];
int n,m,tot,ls[MN],a[MN];

struct BIT{
    private:
        int t[MN];

    public:

    inline int lowbit(int x){
        return x&-x;
    }

    int query(int x){
        int ret=0;
        while(x){
            ret+=t[x];
            x-=lowbit(x);
        }
        return ret;
    }

    void update(int x,int k){
        while(x<MN){
            t[x]+=k;
            x+=lowbit(x);
        }
    }

    int get(int x){
        return t[x];
    }

}b1,b2;

void lisan(){
    sort(ls+1,ls+1+tot);
    tot=unique(ls+1,ls+1+tot)-ls-1;
    for(int i=1;i<=m;i++){
        if(q[i].op){
            q[i].s=lower_bound(ls+1,ls+1+tot,q[i].s)-ls;
        }else q[i].a=lower_bound(ls+1,ls+1+tot,q[i].a)-ls;
    }
}

signed main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        char op;
        int x,y;
        cin>>op;
        if(op=='U'){
            q[i].op=0;
            cin>>q[i].k>>q[i].a;
            ls[++tot]=q[i].a;
        }else{
            q[i].op=1;
            cin>>q[i].c>>q[i].s;
            ls[++tot]=q[i].s;
        }
    }
    lisan();
    for(int i=1;i<=m;i++){
        if(q[i].op==0){
            int x=0;
            if(x=a[q[i].k]){
                b1.update(x,-1);
                b2.update(x,-ls[x]);
            }
            x=a[q[i].k]=q[i].a;
            b1.update(x,1);
            b2.update(x,ls[q[i].a]);
        }else{
            int x=b1.query(tot)-b1.query(q[i].s-1);
            int sum=q[i].s?b2.query(q[i].s-1):0;
            if(sum>=(q[i].c-x)*ls[q[i].s]){
                cout<<"TAK\n";
            }else cout<<"NIE\n";
        }
    }
    return 0;
}

3. 带修主席树

我们总结一下之前学过的：

  • 静态整个序列的 k 小，排序即可。
  • 动态整个序列的 k 小，平衡树或权值线段树即可。
  • 静态区间的 k 小，主席树即可。
  • 动态区间的 k 小？

P2617 Dynamic Rankings

给定一个含有nn 个数的序列a1,a2…ana_1,a_2 \dots a_n，需要支持两种操作：
Q l r k 表示查询下标在区间[l,r][l,r] 中的第kk 小的数
C x y 表示将axa_x 改为yy
强制在线
1≤n,m≤1051\le n,m \le 10^5，1≤l≤r≤n1 \le l \le r \le n，1≤k≤r−l+11 \le k \le r-l+1，1≤x≤n1\le x \le n，0≤ai,y≤1090 \le a_i,y \le 10^9。

所谓动态，就是多了个单点修改。

我们考虑静态是怎么做的，我们对于每个点以其前缀开权值线段树，任意一个区间可以表示为两个权值线段树作差，即Rt[R]−Rt[L−1]Rt[R]-Rt[L-1]。

但是如果我们有了修改呢，如果我们还是用之前的做法，我们要对所有区间的前缀都要做一次修改，极端情况下在下表为 1 的位置修改，我们的一次修改是O(nlog⁡n)O(n\log n)，实际上就是O(qnlog⁡n)O(qn\log n)。

那怎么办？

我们考虑怎么优化这个前缀修改过程…树状数组？

发现上面的前缀的形式都是[1,p][1,p]，这直接树状数组套上去就好了！

这样的话我们修改就能拆成log⁡n\log n 个区间，这样的化修改的时间复杂度就是O(log⁡2n)O(\log ^2 n) 。时间复杂度就是O(qlog⁡2n)O(q\log^2 n)。

但是查询的时候有一点变化，相减是肯定和上面是一样的，但是我们这里不再是两个权值线段树作差，而是两个log⁡n\log n 颗线段树作差，所以我们再跳的时候要跳log⁡n\log n 个儿子。

代码如下，可以看看查询函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
#define ls t[p].lson
#define rs t[p].rson
using namespace std;
const int MN=1e6+15,INF=INT_MAX;
int n,m,tot,a[MN],rt[MN],now[MN],past[MN],ncnt,pcnt,LM;
vector<int> lsan;
struct segtree{
    int lson,rson,val;
}t[MN*100];
struct querynode{
    int op,x,y,z;
}q[MN];

void dolisan(){
    sort(lsan.begin(),lsan.end());
    LM=unique(lsan.begin(),lsan.end())-lsan.begin();
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(lsan.begin(),lsan.begin()+LM,a[i])-lsan.begin();
    }
    for(int i=1;i<=n;i++){
        if(q[i].op==2) q[i].y=lower_bound(lsan.begin(),lsan.begin()+LM,q[i].y)-lsan.begin();
    }

    //for(int i=1;i<=n;i++){
    //    cout<<a[i]<<" ";
    //}
    //cout<<'\n';
}

void change(int &p,int l,int r,int pos,int k){
    if(!p) p=++tot;
    t[p].val+=k;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(mid>=pos) change(ls,l,mid,pos,k);
    else change(rs,mid+1,r,pos,k);
}

int kth(int l,int r,int k){
    if(l==r) return l;
    int sum=0;
    for(int i=1;i<=ncnt;i++){
        sum+=t[t[now[i]].lson].val;
    }
    for(int i=1;i<=pcnt;i++){
        sum-=t[t[past[i]].lson].val;
    }
    int mid=(l+r)>>1;
    if(sum>=k){
        for(int i=1;i<=ncnt;i++){
            now[i]=t[now[i]].lson;
        }
        for(int i=1;i<=pcnt;i++){
            past[i]=t[past[i]].lson;
        }
        return kth(l,mid,k);
    }else{
        for(int i=1;i<=ncnt;i++){
            now[i]=t[now[i]].rson;
        }
        for(int i=1;i<=pcnt;i++){
            past[i]=t[past[i]].rson;
        }
        return kth(mid+1,r,k-sum);
    }
}

void build(){
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j+=lowbit(j)){
            change(rt[j],1,LM-1,a[i],1);
        }
    }
}

int main(){
    lsan.push_back(-INF);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        lsan.push_back(a[i]);
    }
    for(int i=1;i<=m;i++){
        char op;
        cin>>op;
        if(op=='Q'){
            q[i].op=1;
            cin>>q[i].x>>q[i].y>>q[i].z;
        }else{
            q[i].op=2;
            cin>>q[i].x>>q[i].y;
            lsan.push_back(q[i].y);
        }
    }
    dolisan();
    build();

    for(int i=1;i<=m;i++){
        if(q[i].op==1){
            pcnt=ncnt=0;
            for(int j=q[i].x-1;j>0;j-=lowbit(j)){
                past[++pcnt]=rt[j];
            }
            for(int j=q[i].y;j>0;j-=lowbit(j)){
                now[++ncnt]=rt[j];
            }
            cout<<lsan[kth(1,LM-1,q[i].z)]<<'\n';
        }else{
            for(int j=q[i].x;j<=n;j+=lowbit(j)){
                change(rt[j],1,LM-1,a[q[i].x],-1);
            }
            for(int j=q[i].x;j<=n;j+=lowbit(j)){
                change(rt[j],1,LM-1,q[i].y,1);
            }
            a[q[i].x]=q[i].y;
        }
    }
    return 0;
}

练习：动态逆序对。

4. 后言

树状数组的应用还是有很多很多，这里提了几个进阶应用的例子，之后也会稍加整理，感谢阅读！

参考：

  1. qAlex_Weiq大佬的树状数组进阶