SAM后缀自动机学习笔记

0.前言

后缀自动机，在字符串算法中居于一种万能的地位，其本体代码编写较简单，优美的$O(n)$ 构建复杂度，是一类极其有用但难以真正理解的字符串后缀结构。笔者投入了大约一周的时间来学习，现在进行总结复习，看看能不能悟到一些新的东西。

同时后缀自动机本身的难度（10 级）决定了理解较难，笔者同时也是这样的感受。我在编写第一二三章节的时候会尽量用图来解释，尽量减少繁杂的符号化语言。必要的也不会省略。

后缀自动机在做习题的时候，需要有非常扎实的 DS 基础以及面向对象程序设计思想，不然在编写的时候就会炸掉（不然大纲为什么要有这个程序设计思想）。

一些基本约定：

• 本文章默认字符串下标从$1$ 开始。
• 我们用打字机字体表示字符串的内容，如：$s=\texttt{wjyppm1403}$。
• 拼接：$s+t$ 表示将$t$ 拼接$s$ 后。
• 字符集：即构成字符串中字符的集合。
• 空串：不含任何字符的字符串称为空串。
• 子串：在$s$ 开头或末尾删去若干字符得到的字符串称作为$s$ 的子串，$s$ 本身和空串也是$s$ 的子串。我们定义$s[l,r]$ 表示$l \to r$ 上所有字符链接而成子串。
• 匹配：称$t$ 匹配$s$ 当且仅当$t$ 在$s$ 中出现。
• 字符串长度：我们用$|s|$ 来表示$s$ 的长度。

前后缀：

• 前缀：在$s$ 末尾删除若干字符得到的字符串称作$s$ 的前缀，记为$pre$。
• 后缀：在$s$ 开头删除若干字符得到的字符串称作$s$ 的后缀，记为$suf$。
• 最长公共前缀：$\operatorname{LCP}(s,t)$，表示$s,t$ 的最长公共前缀，即最长的$u$ 使得$u$ 为$s,t$ 的前缀。最长公共后缀同理，我们称为$\operatorname{LCS}(s,t)$。LCP 的长度格式为：$|\operatorname{LCP}(s,t)|$。
• 字典序：定义空字符小于任何字符。称$s$ 的 字典序 小于$t$ 当且仅当去掉$\operatorname{LCP}(s,t)$ 后，$s$ 的第一个字符小于 $t$ 的第一个字符。等价于以第 $i$ 个字符作为第 $i$ 关键字比较。

我们先从概念讲起。

1. 自动机

自动机，在 OI 中一般我们涉及的是有限状态自动机（DFA），它拥有有限数量的状态，每个状态代表不同的意义，每个状态可以通过输入自动机指令（严谨来说就是字符），让自动机切换到其他的状态。任意时刻状态机只能处在一个状态。

而有限状态机可以表示为一个有向图：

从图中看出来一个信竞复读机（人类的本质是？）一共包含 5 个状态：学信竟，学 whk，吃吃饭，睡睡觉，摸摸鱼。每种带有箭头的连线，表示可以从当前状态切换到其他的状态，以及切换的条件。

我们列个转移表格：

	学信竟	学 whk	吃吃饭	睡睡觉	摸摸鱼
学信竟			去机房		摆烂时间到
学 whk	信竟时间到			回去午睡
吃吃饭	去食堂	去教室
睡睡觉		回教室	被吵醒
摸摸鱼				回家

表格中左侧第一列为当前状态。
表格中上方第一行为切换的下一个状态。
表格中每行从左到右为状态切换的条件(状态 A 能不能切换到状态B)。

举例：

• 学 whk -> 学信竟：条件（信竟时间到）。
• 学信竟 -> 摸摸鱼：条件（摸鱼时间到）。
• 摸摸鱼 -> 睡睡觉：条件（回家）。

一个自动机，我们应当还有起始状态，在本图中我们的起始状态是 “睡睡觉”。（不准通宵！）

那为啥叫自动呢，是因为只要输入符号和转移规则确定，状态变化是自动的，自动机可以自己通过设定好的路线（即有向图的边权）来进行转移。自动机的工作方式和流程图类似，但是不同的是自动机每一个节点都是一个判定节点，只是一个单纯的状态而非任务。

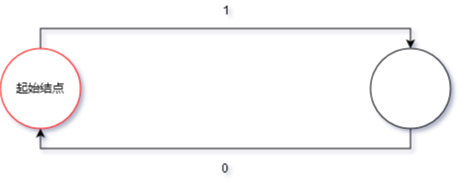
我们借用 Oi-Wiki 的例子，例如完成「判断一个二进制数是不是偶数」的自动机如下：

从起始结点开始，从高到低接受这个数的二进制序列，然后看最终停在哪里。如果最终停在红圈结点，则是偶数，否则不是。

而自动机的实质就是：状态集合（点）+ 转移规则（边）。

在竞赛中的应用我们有 AC 自动机，后缀自动机，DP 套 DP 等。

严谨的定义可以看 Oi-Wiki 的讲解，这里不再深入研究：传送门

2. 后缀自动机

2.1 概念

后缀自动机（SAM）是能够存储和识别一个字符串$S$ 的所有后缀的自动机。

正如我们上面所提到的自动机的定义，后缀自动机也是一个自动机，把节点看作状态，节点之间连的有向边是状态的转移。我们有一个初始状态$st$，从$st$ 通过有向边到达其他所有节点，其中有一些状态是终止状态（即自动机到达这个状态后不会在转移）。任意一条从$st$ 出发到达某个终止状态所经过路径上的字符集合是$S$ 的一个子串。不同的路径代表不同的子串，这些路径与$S$ 的子串一一对应，不多也不少。

这么说有点复杂，读者应该知道 Trie 吧，字典树其实也是一个自动机，我们看看字典树的形状，我们借用 OI-Wiki 的图：

那我们回看上面的自动机表示图，你会发现两者十分相似，事实上 Trie 本身也是一个自动机。而我们把字符串所有后缀子串通过字典树的方法建立的一颗树，我们叫做后缀 Trie，后缀 Trie 也可以看作一种简单的后缀自动机：

如上是$S=\texttt{abcbc}$ 的后缀 Trie，其中绿色节点表示终止节点。算上跟节点需要共 13 个节点，比较浪费空间，原因是因为做了重复存储，如蓝色虚线内圈起来的两个子串是重复的，那么有没有什么更省空间的结构呢？后缀自动机的结构就是我们想要的结构！

SAM 中除了上面的定义，还有一个额外条件：结点数最少。关键就在于如何把上面的图给压缩，压缩点重复的地方。而 SAM 将压缩做到极致，做到$O(n)$ 的节点规模。那么怎么压缩成结点数最少呢？我们把上面的结构用 SAM 的结构表示：

我们把上面后缀 Trie 重复的部分给合并起来，就能够得到上面的一张图。上面的图是一张 DAG，它不仅能表示后缀，还能表示$S$ 的所有子串。任意从初始状态$0$ 开始的路径，如果我们将路径上的所有转移的标号写下来，都会形成$s$ 的一个子串。而每个子串都对应从初始状态开始的某条路径。到达某个状态的路径可能不止一条，在图中也是有表现的，因此我们说一个状态对应一些字符串的集合，这个集合中的字符串分别对应着这些路径。

那么如何得到这个 DAG，这个节点数量是$O(n)$ 的吗。

我尝试建立这个 DAG，每一次我们都尝试添加一个字符，我们从$S=\texttt{a}$ 开始，每次在上一次的末尾添加一个新的节点

这个 DAG 有多少节点？显然每一次加入节点只会增加$O(1)$ 级别的点数，至少有$n+1$ 个点，但是实际上我们建 SAM 的点数会出现冲突的情况，这个时候会复制节点，但是最多复制一次，所有实际上最多也只会有$2n$ 个节点。

SAM 的每一个节点都对应的是原字符串$s$ 的某个子串，读者看图应能自行领会，接下来我们给出几个小定义。

• $\operatorname{substr}(p)$：表示状态$p$ 所有子串的集合。
• $\operatorname{shorest}(p)$：表示状态$p$ 所有子串长度最短的那一个。
• $\operatorname{longest}(p)$：表示状态$p$ 所有子串长度最长的那一个。
• $\operatorname{minlen}(p)$：表示状态$p$ 所有子串长度最短的那一个的长度。
• $\operatorname{len}(p)$：表示状态$p$ 所有子串长度最长的那一个的长度。

2.2 Endpos 等价类

endpos 等价类是 SAM 中关键的地方，通过它我们可以高效地进行建图。

我们定义$\operatorname{endpos}(t)$ 表示字符串$t$ 在$s$ 中所有出现的结束位置的集合，例如当$s=\texttt{"abcbc"}$ 的时候，$\operatorname{endpos}(\texttt{"bc"})=\left\{ 3,5\right\}$，因为$\texttt{"bc"}$ 出现在$s$ 的第$3,5$ 位置。

我们把$s$ 的所有子串的$\operatorname{endpos}$ 都列出来，有：

子串：	a	b	c	ab	bc	cb	abc	bcb	cbc	abcb	bcbc	abcbc
$\operatorname{endpos}$	1	2,4	3,5	2	3,5	4	3	4	5	4	5	5

我们定义空串$\varnothing$ 的$\operatorname{endpos}=\left\{ 1,2,3,4,5 \right\}$ 我们按照 endpos 排序如下：

子串	$\varnothing$	a	ab	b	abc	bc,c	abcb,bcb,cb	abcbc,bcbc,cbc
$\operatorname{endpos}$	1,2,3,4,5	1	2	2,4	3	3,5	4	5

我们把 endpos 相等的称之为等价类，如$\texttt{"c"},\texttt{"bc"}$ 的enpos 等于$\left\{ 3,5 \right\}$ 是等价类。

一个很有趣的事实就是，这样每一个等价类都对应 SAM 的一个状态，读者可以通过 SAM 的图来理解：

接下来我们来阐述 Endpos 等价类所具有的一些特殊性质，endpos 等价类的性质体现的是后缀之间的包含关系。

以下证明来自 Oi-Wiki：

引理 1：同一个等价类中较短子串是较长子串的后缀。

证明是显然成立的，通过定义感性理解：字符串$t$ 在$s$ 中所有出现的结束位置的集合。若结束位置相同，那么必然从这个结束位置向左拓展，必然是后缀。

引理 2：对于两个非空子串$u,w$，假设$|u| \le |w|$。那么，要么$\operatorname{endpos(u)} \cap \operatorname{endpos(w)}=\varnothing$，要么$\operatorname{endpos}(u) \subseteq \operatorname{endpos}(w)$，后者成立当且仅当$u$ 是$w$ 的后缀。

如果集合$\operatorname{endpos}(u)$ 与$\operatorname{endpos}(w)$ 有至少一个公共元素，那么由于字符串$u$ 与$w$ 在相同位置结束，$u$ 是$w$ 的一个后缀。所以在每次$w$ 出现的位置，子串$u$ 也会出现。所以$\operatorname{endpos}(w)\subseteq \operatorname{endpos}(u)$。

引理 3：同一个等价类中子串长度不等，且依次递增 1，覆盖了从最短到最长的子串的区间。即同一个状态对应的子串的长度各不相同，而且是连续的若干自然数，其中较短的总是较长的子串的后缀。

如果等价类中只包含一个子串，引理显然成立。现在我们来讨论子串元素个数大于$1$ 的等价类。

由引理 1，$\operatorname{endpos}$ 相同的两个不同字符串中，必定一长一短，且较短者总是较长者的真后缀。也就是说，等价类中没有等长的字符串。

记$w$ 为等价类中最长的字符串，$u$ 为等价类中最短的字符串。由引理 1，字符串$u$ 是字符串$w$ 的真后缀。现在考虑长度在区间$[\left|u\right|,\left|w\right|]$ 中的$w$ 的任意后缀。容易看出，这个后缀也在同一等价类中，因为这个后缀只能在字符串$s$ 中以$w$ 的一个后缀的形式存在（这是因为较短的后缀$u$ 在$s$ 中只以$w$ 的后缀的形式存在）。因此，由引理 1，这个后缀和字符串$w$ 的$\operatorname{endpos}$ 相同。

2.3 Parent Tree

根据上面 3 个引理，我们知道 endpos 等价类中的子串是具有包含关系，而 SAM 中的节点（或称作状态）就是一个等价类，这样我们通过包含关系把普通后缀树的臃肿给压缩了。

引理 1 和 3 表示了同一个等价类的包含关系，且长度连续，是一个状态就可以表示的。而引理 2 表示状态时如何进行转移的，若$\operatorname{endpos}(v)\subseteq \operatorname{endpos}(u)$ 我们定义转移方向从$u \to v$，即$v$ 是$u$ 的父节点，这里不理解为什么要让大集合向小集合连边可以先了解，后面我们会细说。

下面我们通过$S=\texttt{"abcbc"}$ 来建立一颗 SAM。初始状态$t_{0}$ 是空集$\varnothing$，每一个节点是一个状态，表示一个 endpos 等价类。这棵树只有 8 个点，少于后缀树的 13 个点，我们把这个树称作为母树，即 Parent 树。

这里借用的是 Oi-Wiki 的图，其中 Parent 树中每一个节点我们选取最长字符串来代表状态。我们把表格复制一下列到下面供参考：

子串	$\varnothing$	a	ab	b	abc	bc,c	abcb,bcb,cb	abcbc,bcbc,cbc
$\operatorname{endpos}$	1,2,3,4,5	1	2	2,4	3	3,5	4	5

Parent 树能够完整表达所有子串，有 5 个叶子节点，而 5 个叶子节点对应的endpos 正好是 1 到 5 的完整位置，从根到一个叶子节点的路径上，包含了以这个位置为终点的所有后缀。如最右边的路径。

Parent 树和 AC 自动机的 Fail 树及其相似，如果你知道什么是 Fail 树的话，可以把 Parent 树看作为 Fail 树的压缩版。

但是这里的 Parent 树并不实用，因为我们 SAM 这要这么建立的话那么对于每一个节点我们要存一堆字符串，空间复杂度会爆炸。如果我们通过路径表示子串，像 Trie 树一样多好，让每一条独立的路径对应一个独立的子串，这样即好添加节点，也可以操作啦。而 SAM 通过用路径表示子串来进行的。

我们根据上面的图不难发现 SAM 和 Parent 树及其相似，但是怎么从 Parent 树转化到 SAM 呢？

2.4 后缀链接

后缀链接是我们将 SAM 和 Parent 树之间建立的一个桥梁，事实上，构建 SAM 的过程和母树是息息相关的。

考虑 SAM 上的一个不是根的节点$v$，它的后缀链接（link）定义为它上层的一个节点$u$，其中$u$ 的等价类所包含的子串也是  所包含的子串的后缀。其实就是上文 Parent 树上每个点的父亲。其作用就是将两个不同节点的连续子串连接起来，如下图的母树补充，$v$ 的最短子串长度等于$u$ 的最长字串长度加 1，它们是相邻的两个后缀。

这图糊的已经没救了。

我们再补充几个例子：

$$\mathrm{endpos}(\texttt{"a"}) = \{1\}$$

$$\begin{aligned} \mathrm{endpos}(\texttt{"ab"}) = \{2\} \\ \mathrm{endpos}(\texttt{"abcb", "bcb", "cb"}) = \{4\} \\ \end{aligned} \subsetneq \mathrm{endpos}(\texttt{"b"}) = \{2, 4\}$$

$$\begin{aligned} \mathrm{endpos}(\texttt{"abc"}) = \{3\} \\ \mathrm{endpos}(\texttt{"abcbc", "bcbc", "cbc"}) = \{5\} \\ \end{aligned} \subsetneq \mathrm{endpos}(\texttt{"bc", "c"}) = \{3, 5\}$$

每个节点有且仅有一个后缀链接，沿着后缀链接往上走对应的后缀长度会连续变短，最后到达根，。即，一条从根出发到某个节点的后缀链，表达了一个完整的后缀组合，这是母树的本质。后缀链接构成的树本质上是$\operatorname{endpos}$ 集合构成的一棵树。我们从小集合往大集合建边我们充分利用了 endpos 集合中长度单调递增 1 的性质，并且使得具有上面后缀链的性质。

类似于 AC 自动机的甜蜜组合 Trie+Fail，我们 SAM 就是把转移图和 Parent 树给融合到一起的究极形态。

2.5 构建 SAM

构建的核心思想就是我们前面提到过的增量发，我们在$s[1,i-1]$ 的基础上的 SAM 进行更新，从而得到$s[1,i]$ 的 SAM。构建 SAM 只需要 3 个步骤：

1. 打开 SAM。
2. 插一个字符。
3. 关上 SAM。

冰箱梗，读者不难看出 SAM 的构建是在线算法，我们可以逐个加入字符串中的每个字符，并且在每一步中对应地维护 SAM。

建立 SAM 的关键在于：

• 起点和终点之间的边代表在当前的字符串后添加一个字符。
• 从根到达图中任意路径形成的子串都是$S$ 中的一个子串。
• 要保证每个点的所有字串属于一个 endpos 等价类。
• 要符合 Parent 树的父子关系。

我们这里先给出代码实现与算法流程，让后再逐步说明原理。

一开始我们钦定 SAM 中有一个根节点$t_{0}$，编号就是 0，定义$\operatorname{len}(t_{0})=0,\operatorname{link}(t_{0})=-1$。

让后我们考虑添加一个字符$c$ 拓展 SAM。

1. 令$lst$ 为添加$c$ 之前整个字符串$S$ 所对应的节点（即上一个所更新的节点）。
2. 创建一个新的状态，并将$\operatorname{len}(cur)=\operatorname{len}(lst)+1$。
3. 从$lst$ 开始遍历遍历后缀链接，如果当前结点 $v$ 没有标记字符 $c$ 的出边，创建一条 $v\to cur$ 的边，标记为 $c$。
4. 如果遍历到了$t_{0}$，令$\operatorname{link}(cur)=0$，跳到第 8 步。
5. 如果当前结点 $v$ 已经有了标记字符 $c$ 的出边，停止遍历，并把这个结点标记为 $p$，标记 $p$ 沿着标记字符 $c$ 的出边到达的点为 $q$。
6. 如果$\operatorname{len}(p)+1=\operatorname{len}(q)$，令$\operatorname{link}(cur)=q$，跳到第 8 步。
7. 否则，复制状态$q$ 到一个新的状态里$nq$（包括 link 与它在 DAG 上的出边），将$\operatorname{len}(nq)=\operatorname{len}(p)+1$。赋值之后在令$\operatorname{link}(q)=nq,\operatorname{link}(cur)=nq$。从 $p$ 遍历后缀链接，设当前遍历到的点为 $v$，若 $v$ 有标记为 $c$ 的出边且$v\to q$，则重定向这条边为 $v \to nq$。若 $v$ 没有标记为 $c$ 的出边或者 $v$ 的标记为 $c$ 的出边所到达的点不是 $q$ ，停止遍历，转 8。
8. 令$lst=cur$，结束。

代码实现如下：

int newnode(){
    int cur=++tot;
    memset(nxt[cur],0,sizeof(nxt[cur]));
    return cur;
}

int clone(int from){
    int cur=++tot;
    fa[cur]=fa[from];
    memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
    return cur;
}

void extend(int c){
    int cur=newnode(); //步骤1
    len[cur]=len[lst]+1;//步骤2
    int p=lst;
    while(p!=-1&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];//步骤3
    if(p==-1) fa[cur]=0;//步骤4
    else{
        int q=nxt[p][c];//步骤5
        if(len[q]==len[p]+1) fa[cur]=q;//步骤6
        else{//步骤7
            int nq=clone(q);
            len[nq]=len[p]+1;
            fa[q]=fa[cur]=nq;
            while(p!=-1&&nxt[p][c]==q) nxt[p][c]=nq,p=fa[p];
        }
    }
    lst=cur;//步骤8
}

关于每一步的解释，大家可以去看后缀自动机(SAM)奶妈式教程 - ZTer 的教程，这里就不再详细展开了，以防篇幅过长。

实现代码如下：

struct SAM{
    int nxt[MN][26],fa[MN],len[MN],tot,lst;
    vector<int> adj[MN];

    void init(){
        tot=0;
        lst=0;
        fa[0]=-1;
        len[0]=0;
        memset(nxt[0],0,sizeof(nxt[0]));
        cnt_init[0]=0;
    }

    int newnode(){
        int cur=++tot;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        return cur;
    }

    int clone(int from){
        int cur=++tot;
        fa[cur]=fa[from];
        memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
        return cur;
    }

    void extend(int c){
        int cur=newnode();
        len[cur]=len[lst]+1;
        int p=lst;
        while(p!=-1&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
        if(p==-1) fa[cur]=0;
        else{
            int q=nxt[p][c];
            if(len[q]==len[p]+1) fa[cur]=q;
            else{
                int nq=clone(q);
                len[nq]=len[p]+1;
                while(p!=-1&&nxt[p][c]==q) nxt[p][c]=nq,p=fa[p];
                fa[q]=fa[cur]=nq;
            }
        }
        lst=cur;
    }

    void inittree(){// 构建 link 树
        for(int i=0;i<=tot;i++){
            adj[i].clear();
            cnt[i]=-1;
        }
        for(int i=1;i<=tot;i++){
            adj[fa[i]].push_back(i);
        }
    }
}sam;

3. 广义后缀自动机

这里讲的是在线做法，因为在线做法只需要在原先的板子上更改一下就可以了。

广义后缀自动机是后缀自动机的升级版，可以同时表示多个字符串所有字串集合的数据结构。

而假的在线构建方法及其简单，就是插入完一个字符串后把$last$ 指针指向根节点，接着插就可以了，但是这样构建的 SAM 虽然能用，但是并不满足前面我们所提过的最小结构。具体来说，有以下两种情况：

• 一个等价类被拆成若干个节点，子串信息被分散。
• 出现空节点。

注意到上面的节点的问题在于重复的前缀会被拆分或者重复创建新节点。我们可以通过在 expand 函数中添加特判，重复的前缀会被特判处理到，这样我们就可以对了。

以下是 expand 代码：

int extend(int c,int lst){
    if(nxt[lst][c]&&len[nxt[lst][c]]==len[lst]+1) return nxt[lst][c]; // / 如果节点已经存在，且 len 值相对应，即连续转移，则直接转移。
    int cur=newnode(),p=lst,flag=0,q,nq;
    len[cur]=len[p]+1;
    while(p&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
    if(!p){
        fa[cur]=1;
    }else{
        q=nxt[p][c];
        if(len[q]==len[p]+1){
            fa[cur]=q;
        }else{
            if(p==lst) flag=1,cur=0,tot--;
            nq=clone(q);
            len[nq]=len[p]+1;
            fa[q]=fa[cur]=nq;
            while(p&&nxt[p][c]==q){
                nxt[p][c]=nq;
                p=fa[p];
            }
        }
    }
    return flag?nq:cur; //// 如果 len[las][it] 存在，则 cur 是空壳，返回 nq 即可
}

上面的方法本质就是对匹配串建出 trie 后进行 dfs 构建 SAM。

4. 常用技巧与结论

求本质不同子串个数

根据 SAM 的性质，每一个字串对应的是唯一一个状态，那么答案就是$\operatorname{len}(p)-\operatorname{len}(fa_{p})$。其中$fa_{p}$ 表示 link 树上$p$ 状态的父亲。

线段树合并维护 endpos 集合。

有一些题目我们需要知道 endpos 集合内的内容具体是什么，以刻画每个子串在字符串中所有出现位置的信息。

根据上面所提到的，endpos 集合构建出来的树就是 link 树。为此，我们可以通过在 link 树上进行线段树合并的方式可以得到每个状态的 endpos 集合。

同时注意，线段树合并会破坏原有线段树的结构，如果我们需要保留每一个节点的 endpos 集合的话，我们线段树合并的形式应当是新建节点的方式而不是在原有结构直接复制的方式。

快速定位一个子串的对应状态

给定区间$[l,r]$，求$s_{[l,r]}$ 在 SAM 上对应的状态，在构建 SAM 时候像 AC 自动机一样预处理$s_{[1,i]}$ 所表示的状态$pos_i$，我们从$pos_r$ 上倍增二分找到第一个$len \ge r-l+1$ 的状态，这个状态就是我们所求的状态。

桶排确定 dfs 顺序

link 树上父亲的 len 值一定小于儿子的，但编号小的不一定 len 也小！考虑对于所有结点按照 len 值从大到小进行桶排序，让后按照顺序合并每个状态及其父亲，效果等同于 link 树自底向上合并信息的过程。

5. 实战演练

P3804 【模板】后缀自动机 (SAM)

答案就是$\sum\limits_{|\operatorname{endpos}(p)|\ge 2} \operatorname{len}(p)\times |\operatorname{endpos}(p)|$，求出 endpos 集合大小即可，具体怎么求可以看代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=3e6+15;
int n;
ll ans;
string s;

struct SAM{
    int nxt[MN][26],fa[MN],len[MN],cnt[MN],tot,lst;
    int cnt_init[MN];
    vector<int> adj[MN];

    void init(){
        tot=0;
        lst=0;
        fa[0]=-1;
        len[0]=0;
        memset(nxt[0],0,sizeof(nxt[0]));
        cnt_init[0]=0;
    }

    int newnode(){
        int cur=++tot;
        cnt_init[cur]=1;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        return cur;
    }

    int clone(int from){
        int cur=++tot;
        fa[cur]=fa[from];
        cnt_init[cur]=0;
        memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
        return cur;
    }

    void extend(int c){
        int cur=newnode();
        len[cur]=len[lst]+1;
        int p=lst;
        while(p!=-1&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
        if(p==-1) fa[cur]=0;
        else{
            int q=nxt[p][c];
            if(len[q]==len[p]+1) fa[cur]=q;
            else{
                int nq=clone(q);
                len[nq]=len[p]+1;
                while(p!=-1&&nxt[p][c]==q) nxt[p][c]=nq,p=fa[p];
                fa[q]=fa[cur]=nq;
            }
        }
        lst=cur;
    }

    void inittree(){
        for(int i=0;i<=tot;i++){
            adj[i].clear();
            cnt[i]=-1;
        }
        for(int i=1;i<=tot;i++){
            adj[fa[i]].push_back(i);
        }
    }

    int dfs(int u){
        if(cnt[u]!=-1) return cnt[u];
        int sum=cnt_init[u];
        for(auto v:adj[u]){
            sum+=dfs(v);
        }
        cnt[u]=sum;
        if(cnt[u]!=1){
            ans=max(ans,1ll*cnt[u]*len[u]);
        }
        return cnt[u];
    }

}sam;

int main(){
    cin>>s;
    n=s.length();
    s=" "+s;
    sam.init();
    for(int i=1;i<=n;i++){
        sam.extend(s[i]-'a');
    }
    sam.inittree();
    sam.dfs(0);
    cout<<ans;
    return 0;
}

P6139 【模板】广义后缀自动机（广义 SAM）

本质不同子串个数我们已经提到过了，这里不再叙述。

直接放个板子：

struct gySAM{
    int nxt[MN][26],fa[MN],pos[MN],len[MN],tot;
    vector<int> adj[MN];

    void init(){
        for(int i=0;i<=tot;i++){
            adj[i].clear();
            fa[i]=pos[i]=len[i]=0;
            memset(nxt[i],0,sizeof(nxt[i]));
        }
        tot=1;
    }

    gySAM(){
        init();
    }

    int newnode(){
        int cur=++tot;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        return cur;
    }

    int clone(int from){
        int cur=++tot;
        fa[cur]=fa[from];
        memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
        return cur;
    }

    int extend(int c,int lst){
        if(nxt[lst][c]&&len[nxt[lst][c]]==len[lst]+1) return nxt[lst][c];
        int cur=newnode(),p=lst,flag=0,q,nq;
        len[cur]=len[p]+1;
        while(p&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
        if(!p){
            fa[cur]=1;
        }else{
            q=nxt[p][c];
            if(len[q]==len[p]+1){
                fa[cur]=q;
            }else{
                if(p==lst) flag=1,cur=0,tot--;
                nq=clone(q);
                len[nq]=len[p]+1;
                fa[q]=fa[cur]=nq;
                while(p&&nxt[p][c]==q){
                    nxt[p][c]=nq;
                    p=fa[p];
                }
            }
        }
        return flag?nq:cur;
    }

    void inittree(){
        for(int i=2;i<=tot;i++){
            adj[fa[i]].push_back(i);
        }
    }

    void insert(string s){
        int len=s.length(),lst=1;
        s=" "+s;
        for(int i=1;i<=len;i++){
            lst=extend(s[i]-'a',lst);
        }
    }

}sam;

P4070 [SDOI2016]生成魔咒

答案就是$\operatorname{len}(p)-\operatorname{len}(fa_{p})$。其中$fa_{p}$ 表示 link 树上$p$ 状态的父亲。

void extend(int c){
    int cur=++tot;
    len[cur]=len[lst]+1;
    cnt_init[cur]=1;
    nxt[cur].clear();
    int p=lst;
    while(p!=-1&&!nxt[p][c]){
        nxt[p][c]=cur;
        p=fa[p];
    }
    if(p==-1) fa[cur]=0;
    else{
        int q=nxt[p][c];
        if(len[q]==len[p]+1){
            fa[cur]=q;
        }
        else{
            int nq=++tot;
            len[nq]=len[p]+1;
            nxt[nq]=nxt[q];
            fa[nq]=fa[q];
            cnt_init[nq]=0;
            while(p!=-1&&nxt[p][c]==q){
                nxt[p][c]=nq;
                p=fa[p];
            }
            fa[q]=fa[cur]=nq;
        }
    }
    lst=cur;
    ans+=len[cur]-len[fa[cur]];
}

其中 cnt_init 没有任何用，只是复制板子复制上的。

P4022 [CTSC2012]熟悉的文章

典。

战术二分答案$mid$，问题转化为判断这个$L$ 是否可行，考虑 DP。设$f_{i}$ 表示文章$i$ 前缀最长符合限制的匹配长度，有转移方程：

$$\begin{aligned}f_{i} & =\max \{ f_{j}+i-(j+1)+1,f_{i-1} \} & j \in [i-mxlen(i),i-mid]\end{aligned}$$

其中$mxlen$ 表示以$i$ 为结尾的字符串出现在模板串中的最长长度，用 SAM 类似于 LCS 的方法即可。

转移是$O(n^2)$ 的，可以通过单调队列优化成$O(n)$。时间复杂度$O(n\log n)$。

#include <bits/stdc++.h>
using namespace std;
constexpr int MN = 5e5 + 15;
int n, m, len, f[MN], ql, qr, q[MN], L[MN];

struct SAM {
    int nxt[MN][3], fa[MN], cnt[MN], len[MN], cnt_init[MN], tot, lst;

    void init() {
        tot = lst = 0;
        fa[0] = -1;
        len[0] = 0;
        memset(nxt[0], 0, sizeof(nxt[0]));
        cnt_init[0] = 0;
    }

    void find(string s, int slen) {
        int p = 0, now = 0;
        for (int i = 0; i < slen; i++) {
            int x = s[i] - '0';
            if (x < 0 || x > 1) continue;
            if (nxt[p][x]) {
                now++;
                p = nxt[p][x];
            } else {
                for (; p != -1 && !nxt[p][x]; p = fa[p]);
                if (p == -1) p = 0, now = 0;
                else now = len[p] + 1, p = nxt[p][x];
            }
            L[i + 1] = now;
        }
    }

    void extend(int c) {
        int cur = ++tot;
        len[cur] = len[lst] + 1;
        cnt_init[cur] = 1;
        memset(nxt[cur], 0, sizeof(nxt[cur]));
        int p = lst;
        while (p != -1 && !nxt[p][c]) {
            nxt[p][c] = cur;
            p = fa[p];
        }
        if (p == -1) {
            fa[cur] = 0;
        } else {
            int q = nxt[p][c];
            if (len[q] == len[p] + 1) {
                fa[cur] = q;
            } else {
                int nq = ++tot;
                len[nq] = len[p] + 1;
                memcpy(nxt[nq], nxt[q], sizeof(nxt[q]));
                fa[nq] = fa[q];
                cnt_init[nq] = 0;
                while (p != -1 && nxt[p][c] == q) {
                    nxt[p][c] = nq;
                    p = fa[p];
                }
                fa[q] = fa[cur] = nq;
            }
        }
        lst = cur;
    }
} sam;

bool check(int mid) {
    int ql = 0, qr = -1;
    for (int i = 0; i <= mid - 1; i++) f[i] = 0;
    for (int i = mid; i <= len; i++) {
        f[i] = f[i - 1];
        while (ql <= qr && (f[i - mid] - (i - mid)) > (f[q[qr]] - q[qr])) qr--;
        q[++qr] = i - mid;
        while (ql <= qr && q[ql] < (i - L[i])) ql++;
        if (ql <= qr) f[i] = max(f[i], f[q[ql]] - q[ql] + i);
    }
    return f[len] * 10 >= len * 9;
}

int main() {
    cin >> n >> m;
    sam.init();
    for (int i = 1; i <= m; i++) {
        string s;
        cin >> s;
        for (auto c : s) {
            sam.extend(c - '0');
        }
        sam.extend(2); 
    }

    for (int i = 1; i <= n; i++) {
        string s;
        cin >> s;
        len = s.length();
        sam.find(s, len);
        int l = 1, r = len+1;
        while (l + 1 < r) {
            int mid = (l + r) >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid;
            }
        }
        cout << l << '\n';
    }

    return 0;
}

SP8093 JZPGYZ - Sevenk Love Oimaster

重要结论，SAM 上暴力跳链是$O(n\sqrt{n})$ 的，下面是证明：

设一个串长度为$L$，那么覆盖$L^2$ 的路径长度；同时又有SAM一个节点最多被覆盖后缀树上儿子个数次，因此这个上限是 $|S|$（SAM大小）

那么跳链的复杂度就是$\min(L^2,|S|)=L\cdot \min(L,\dfrac{|S|}{L})$ 的，由均值不等式不难得出不超过$\sqrt{S}$。

把所有串丢进广义SAM，对每一个节点打标记，记录组后一次它暴力跳到的串的编号。如果已经相同就不跳了。对于每一个询问，沿着转移边走，走到终止节点的覆盖次数即为答案。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=5e6+15;
struct Query{
    int l,r,id;
};
int n,m,pre[MN],ans[MN];
vector<int> adj[MN];
vector<int> col[MN];
vector<Query> qry;

struct gySAM{
    int nxt[MN][26],fa[MN],pos[MN],len[MN],cnt[MN],tot;
    int cnt_init[MN];

    void init(){
        for(int i=0;i<=tot;i++) adj[i].clear();
        tot=1; // 初始状态设为1
        fa[1]=-1;
        len[1]=0;
        memset(nxt[1],0,sizeof(nxt[1]));
        cnt_init[1]=0;
    }

    int extend(int c,int lst){
        if(nxt[lst][c] && len[nxt[lst][c]] == len[lst]+1) return nxt[lst][c];
        int cur=++tot;
        len[cur]=len[lst]+1;
        cnt_init[cur]=1;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        int p=lst;
        while(p != -1 && !nxt[p][c]){
            nxt[p][c]=cur;
            p=fa[p];
        }
        if(p == -1) fa[cur]=1; // 初始状态是1
        else{
            int q=nxt[p][c];
            if(len[q] == len[p]+1) fa[cur]=q;
            else{
                int nq=++tot;
                len[nq]=len[p]+1;
                memcpy(nxt[nq],nxt[q],sizeof(nxt[q]));
                fa[nq]=fa[q];
                cnt_init[nq]=0;
                while(p != -1 && nxt[p][c]==q){
                    nxt[p][c]=nq;
                    p=fa[p];
                }
                fa[q]=fa[cur]=nq;
            }
        }
        return cur;
    }

    void inittree(){
        for(int i=0;i<=tot;i++) adj[i].clear();
        for(int i=2;i<=tot;i++) adj[fa[i]].push_back(i);
    }
}sam;

struct BIT{
    int t[MN];

    int lowbit(int x){
        return x&-x;
    }

    void modify(int x,int k){
        while(x<MN){
            t[x]+=k;
            x+=lowbit(x);
        }
    }

    int query(int x){
        int ret=0;
        while(x){
            ret+=t[x];
            x-=lowbit(x);
        }
        return ret;
    }

}bit;

namespace Tree{
    int siz[MN],dfn[MN],id[MN],dtot;

    void dfs(int u,int pre){
        dfn[u]=++dtot;
        id[dtot]=u;
        siz[u]=1;
        for(auto v:adj[u]){
            if(v==pre) continue;
            dfs(v,u);
            siz[u]+=siz[v];
        }
    }
}using namespace Tree;

bool cmp(Query x,Query y){
    return x.r<y.r;
}

int main(){
    sam.init();
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        string s;
        cin>>s;
        int lst=1; // 初始状态设为1
        for(auto c:s){
            lst=sam.extend(c-'a',lst);
            col[lst].push_back(i);
        }
    }
    sam.inittree();
    dtot=0;
    dfs(1,-1); // DFS根节点设为1
    for(int i=1;i<=m;i++){
        string s;
        cin>>s;
        int p=1; // 初始状态设为1
        for(auto c:s){
            p=sam.nxt[p][c-'a'];
            if(!p) break;
        }
        if(p){
            qry.push_back({dfn[p],dfn[p]+siz[p]-1,i});
        }
    }
    sort(qry.begin(),qry.end(),cmp);
    int current_p=1; // 维护全局的current_p
    for(auto q:qry){
        while(current_p <= q.r){
            int u=id[current_p];
            for(auto c:col[u]){
                if(pre[c]) bit.modify(pre[c],-1);
                bit.modify(current_p,1);
                pre[c]=current_p;
            }
            current_p++;
        }
        ans[q.id]=bit.query(q.r)-bit.query(q.l-1);
    }
    for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
    return 0;
}

P3649 [APIO2014] 回文串

首先建 SAM，让后跑 manacher，一旦出现回文串我们就放到 SAM 上查询。

现在问题转化为快速查询一个字串的出现次数，用上面我们提到的技巧倍增二分即可，时间复杂度$O(n \log n)$。

也有纯 SAM 的，但是理解过于复杂，看不懂 www。

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=6e5+15;
int n,m,r[MN],poss[MN];
long long ans;
int pre[20][MN];
char p[MN];
string s;

struct SAM{
    int nxt[MN][26],len[MN],c[MN],cnt[MN],id[MN],pos[MN],fa[MN],tot,lst;

    void init(){
        tot=lst=1;
    }

    int newnode(){
        int cur=++tot;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        return cur;
    }

    int clone(int from){
        int cur=newnode();
        fa[cur]=fa[from];
        memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
        return cur;
    }

    void expand(int c){
        int cur=newnode();
        len[cur]=len[lst]+1;
        cnt[cur]=1;
        int p=lst;
        while(p&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
        if(!p){
            fa[cur]=1;
        }else{
            int q=nxt[p][c];
            if(len[q]==len[p]+1){
                fa[cur]=q;
            }else{
                int nq=clone(q);
                len[nq]=len[p]+1;
                fa[cur]=fa[q]=nq;
                while(p&&nxt[p][c]==q){
                    nxt[p][c]=nq,p=fa[p];
                }
            }
        }
        lst=cur;
    }

    void getcnt(){
        for(int i=1;i<=tot;i++) c[len[i]]++;
        for(int i=1;i<=n;i++) c[i]+=c[i-1];
        for(int i=1;i<=tot;i++) id[c[len[i]]--]=i;
        for(int i=tot;i>=1;i--){
            cnt[fa[id[i]]]+=cnt[id[i]];
        }
    }

    void initst(){
        for(int i=1;i<=tot;i++) pre[0][i]=fa[i];
        for(int i=1;i<20;i++){
            for(int j=1;j<=tot;j++){
                pre[i][j]=pre[i-1][pre[i-1][j]];
            }
        }
    }

    void find(int l,int r){
        if(l<1||r>n) return;
        int slen=r-l+1,now=pos[r];
        for(int i=19;i>=0;i--){
            if(pre[i][now]&&len[pre[i][now]]>=slen) now=pre[i][now];
        }
        ans=max(ans,1ll*cnt[now]*(r-l+1));
    }
    
}sam;

void manacher(){
    p[++m]='@';
    for(int i=1;i<=n;i++){
        p[++m]='#';
        p[++m]=s[i];
        poss[m]=i;
    }
    p[++m]='#',p[++m]='$';
    int pos=0,mx=0;
    for(int i=1;i<=m;i++){
        if(i<mx) r[i]=min(mx-i,r[pos*2-i]);
        else r[i]=1;
        sam.find(poss[i-r[i]+2],poss[i+r[i]-2]);
        while(p[i-r[i]]==p[i+r[i]]){
            r[i]++;
            sam.find(poss[i-r[i]+2],poss[i+r[i]-2]);
        }
        if(i+r[i]>mx){
            mx=i+r[i],pos=i;
        }
    }
}

signed main(){
    cin>>s;
    sam.init();
    n=s.length();
    s=" "+s;
    for(int i=1;i<=n;i++){
        sam.expand(s[i]-'a');
        sam.pos[i]=sam.lst;
    }
    sam.initst();
    sam.getcnt();
    manacher();
    cout<<ans;

    return 0;
}

P5546 [POI 2000] 公共串

战术建立广义 SAM，所有串的最长公共子串长度肯定不会超过最短的那个串，所以可以拿最短的那个串建机，然后把其他串放到上面匹配，让后记录每一个点经过的最小值，让后答案就是节点最小值的最大值。

CF1037H Security

战术建立 SAM，对于每个询问串，我们要在原串中求出一个字典序最小的串，使得其字典序比他大。考虑在 SAM 的 DAG 转移图上贪心从小到大选取点走，同时还需要利用线段树合并来判断当前字符串是否作为$[l,r]$ 的子串出现过，时间复杂度$O(n \log n)$。

Submission #327862208 - Codeforces

CF700E Cool Slogans

神仙结论题。

link 树有一个结论，若$p$ 是$q$ 的祖先，则状态$p$ 所表示的子串集合在$\operatorname{longest}(q)$ 中出现次数与出现位置相同。

既然都这么说了，考虑建立 SAM，在 link 树上从根向下进行 dp，设$f_{i}$ 表示到节点$i$ 时最大值。

如果一个父节点的子串在子节点的子串中出现了至少两次，则转移时 $f$ 加一，否则不变。

考虑如何判断至少出现两次，根据我们上面的结论，出现次数与出现位置相同。考虑设此时节点为$x$，那么找到$x$ 对应的 endpos 中任意一个位置$pos$，则$pos$ 的子串一定在 link 树父亲节点出现了一次，那么我们只需要在$[pos-len(x)+len(fa_{x}),pos-1]$ 中出现即可，用线段树合并可以轻松解决，时间复杂度$O(n \log n)$。

Submission #327902686

UVA1673 数字子串的和 str2int

建立广义后缀自动机，让后现在问题是计数，考虑 link 树上计数 DP。

设$f_{i}$ 表示 SAM 上点$i$ 代表的转台结尾的数字之和，$g_{i}$ 表示不同的数字数目。

有转移：

$$g_{y}=\sum\limits_{nxt[x][c]=y} g_{x}$$

$$f_{y}\sum\limits_{nxt[x][c]=y} f_{x}\times 10+g_{x}\times c$$

初始化$f[1]=0,g[1]=1$，答案即为$\sum\limits f_{i}$。

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=1e6+15,MOD=2012;
int n,f[MN],g[MN];

struct gySAM{
    int nxt[MN][26],c[MN],id[MN],fa[MN],len[MN],mxl,tot;
    vector<int> adj[MN];

    void init(){
        for(int i=0;i<=tot;i++){
            adj[i].clear();
            fa[i]=g[i]=f[i]=len[i]=c[i]=id[i]=0;
            memset(nxt[i],0,sizeof(nxt[i]));
        }
        tot=1;
        mxl=0;
        g[1]=1;
    }

    gySAM(){
        init();
    }

    int newnode(){
        int cur=++tot;
        f[cur]=g[cur]=0;
        memset(nxt[cur],0,sizeof(nxt[cur]));
        return cur;
    }

    int clone(int from){
        int cur=newnode();
        fa[cur]=fa[from];
        memcpy(nxt[cur],nxt[from],sizeof(nxt[from]));
        return cur;
    }

    int extend(int c,int lst){
        if(nxt[lst][c]&&len[nxt[lst][c]]==len[lst]+1) return nxt[lst][c];
        int cur=newnode(),p=lst,flag=0,q,nq;
        len[cur]=len[p]+1;
        while(p&&!nxt[p][c]) nxt[p][c]=cur,p=fa[p];
        if(!p){
            fa[cur]=1;
        }else{
            q=nxt[p][c];
            if(len[q]==len[p]+1){
                fa[cur]=q;
            }else{
                if(p==lst) flag=1,cur=0,tot--;
                nq=clone(q);
                len[nq]=len[p]+1;
                fa[q]=fa[cur]=nq;
                while(p&&nxt[p][c]==q){
                    nxt[p][c]=nq;
                    p=fa[p];
                }
            }
        }
        return flag?nq:cur;
    }

    void insert(string s){
        int len=s.length(),lst=1;
        s=" "+s;
        mxl=max(mxl,len);
        for(int i=1;i<=len;i++){
            lst=extend(s[i]-'0',lst);
        }
    }

    void initc(){
		for(int i=1; i<=tot; ++i) c[len[i]]++;
		for(int i=0; i<=mxl; ++i) c[i]=0;
		for(int i=1; i<=tot; ++i) c[len[i]]++;
		for(int i=1; i<=mxl; ++i) c[i]+=c[i-1];
		for(int i=1; i<=tot; ++i) id[c[len[i]]--]=i;    
    }

    void solve(){
        for(int i=1;i<=tot;i++){
            int u=id[i];
            cerr<<u<<" ";
            for(int j=0;j<10;j++){
                if((u==1&&!j)||!nxt[u][j]) continue;
                (f[nxt[u][j]]+=g[u]*j+f[u]*10)%=MOD;
                (g[nxt[u][j]]+=g[u])%=MOD;
            }
        }
    }
}sam;


void solve(){
    sam.init();
    for(int i=1;i<=n;i++){
        string s;
        cin>>s;
        sam.insert(s);
    }
    sam.initc();
    sam.solve();
    int ans=0;
    for(int i=1;i<=sam.tot;i++) (ans+=f[i])%=MOD;
    cout<<ans<<'\n';
}

signed main(){
    while(cin>>n){
        solve();
    }

    return 0;
}

CF666E Forensic Examination

SAM 技巧大集合。首先考虑建出$s,t_{i}$ 的广义 SAM，目标是查询$S$ 的子串在模板串区间的哪个串里出现次数最多。由于查询的是一个区间次数，考虑线段树合并维护，让后子串查询状态可以用倍增二分的技巧跳到对应状态在线段树上查询最大值就可以了。时间复杂度$O(n \log n)$。

Submission #327723329 - Codeforces

P5576 [CmdOI2019] 口头禅 - 洛谷

command_block 题解

做法 3 好写，真的。

P8368 [LNOI2022] 串 - 洛谷

题解：P8368 [LNOI2022] 串 - 洛谷专栏 我的题解不是因为我不想复制，篇幅过长。

6. 后言

留一点练习题：

• 轻重子树分治：P4482 [BJWC2018] Border 的四种求法 - 洛谷
• 后缀树优化建图：P5284 [十二省联考 2019] 字符串问题 - 洛谷
• 线段树合并：P4770 [NOI2018] 你的名字 - 洛谷
• LCT 在 link 树的应用（不会的可以用 ODT）：P6292 区间本质不同子串个数 - 洛谷
• 性质套 SAM：P3346 [ZJOI2015]诸神眷顾的幻想乡
• 第$k$ 小：P3975 [TJOI2015]弦论

参考

• 罗勇军的《算法竞赛》
• 常见字符串算法 II：自动机相关 - qAlex_Weiq
• zzctommy的后缀自动机练习记录
• 后缀自动机学习笔记 | Menci’s OI Blog
• Oi-Wiki
• 后缀自动机练习记录 - zzctommy - 博客园
• command_block 题解
• 神秘的物质