斜率优化与WQS带权二分优化DP

1.前言

本文章图较多！
动态规划在转移的时候，我们称最终转移过来的状态为决策点。
而对于斜率优化和WQS带权二分都是利用凸包和切线的概念来优化DP

[!WARNING]
斜率优化和WQS带权二分几乎完全不同，请不要混淆！

2.凸包与切线

2.1 凸包

凸包是什么呢？其实就是字面意思，一个凸起的小包，但是这个是描述图形的。如下图：

严谨来说，应当是其图形的切线斜率是具有单调性，其导函数$f'(x)$具有单调性。

但是在OI中一般凸包都不是光滑的，如下图。

但是也还是可以满足定义的即：

经过相邻两点的直线斜率有单调性

2.2 切线与一次函数

2.2.1 一次函数

$$y=kx+b$$

• $k$：斜率
• $b$：截距（$y$ 轴交点）

2.2.2 切线

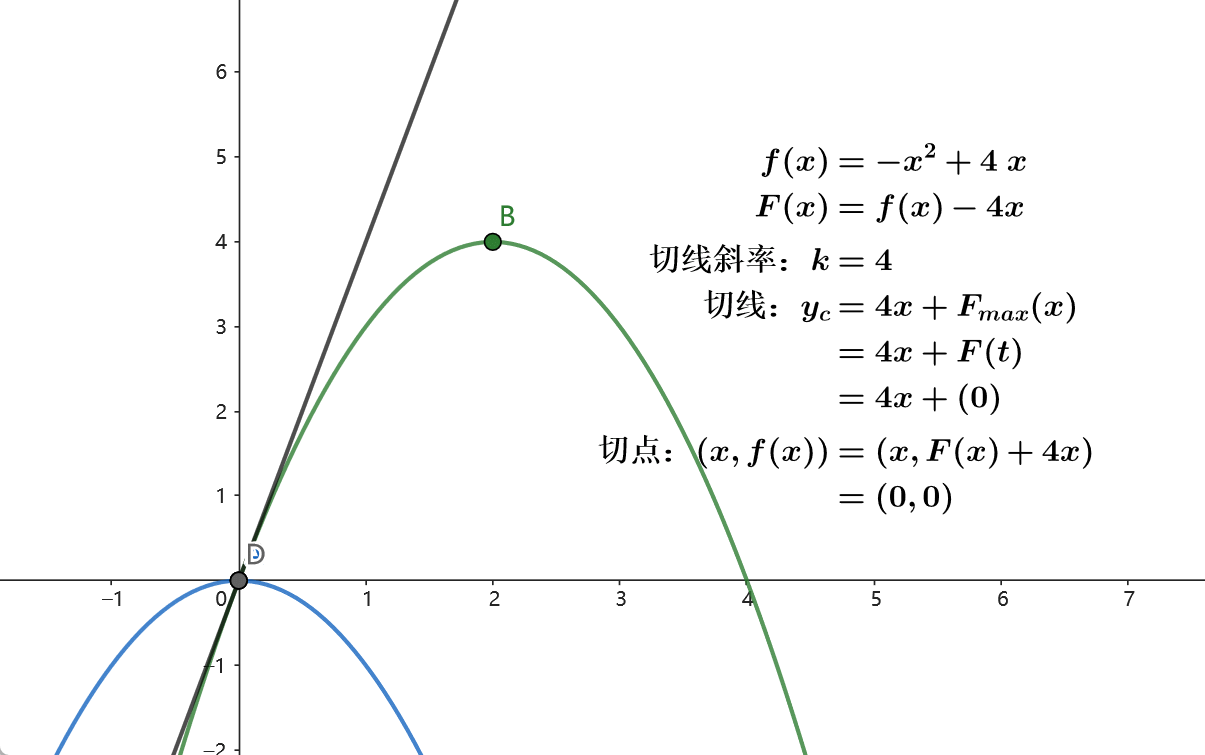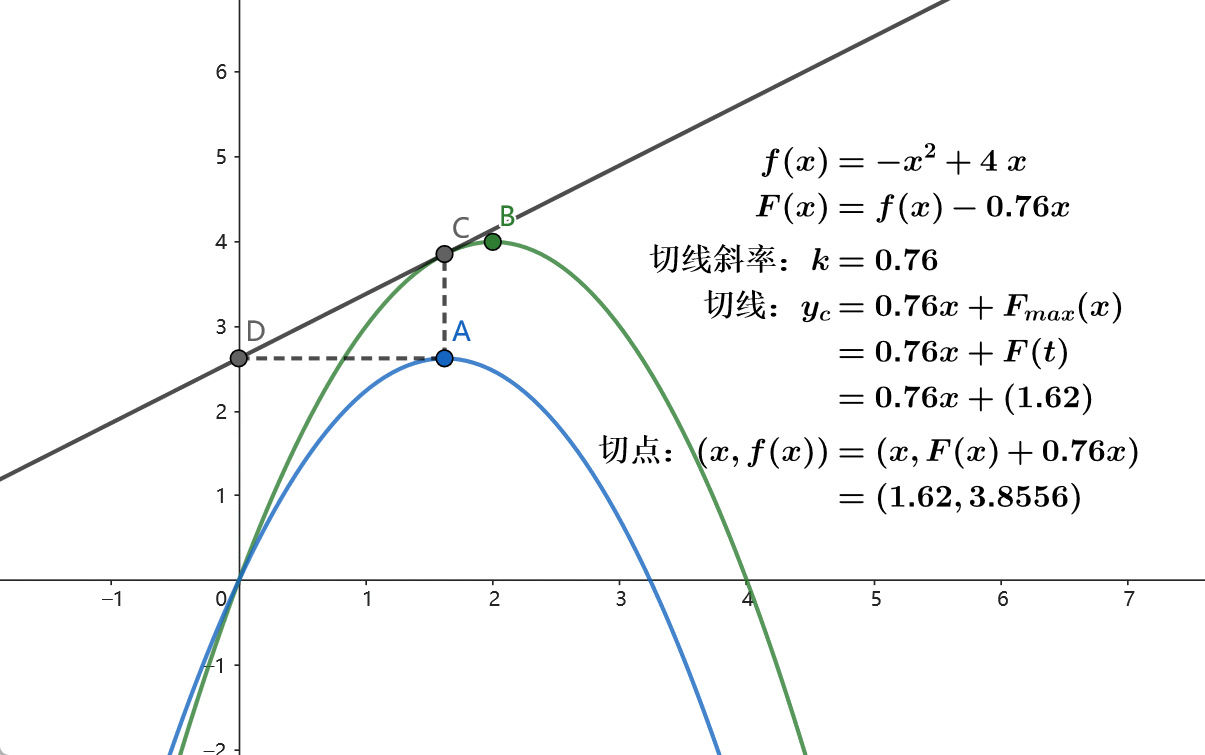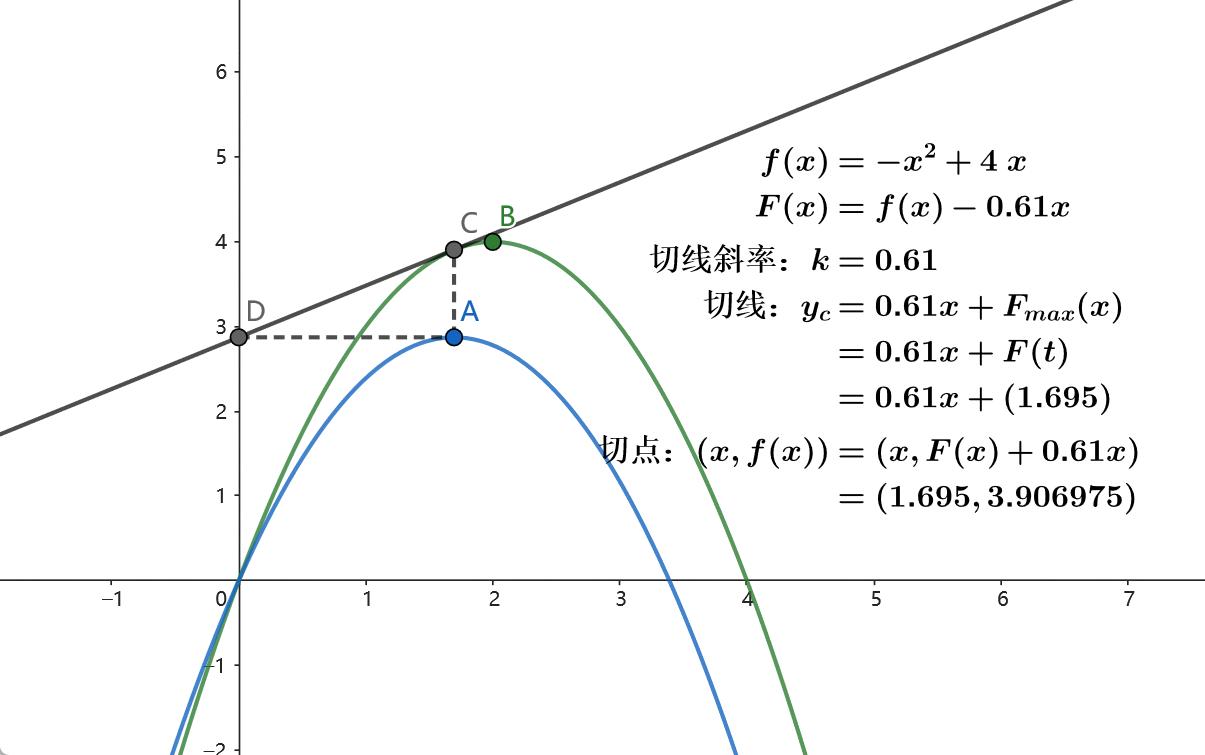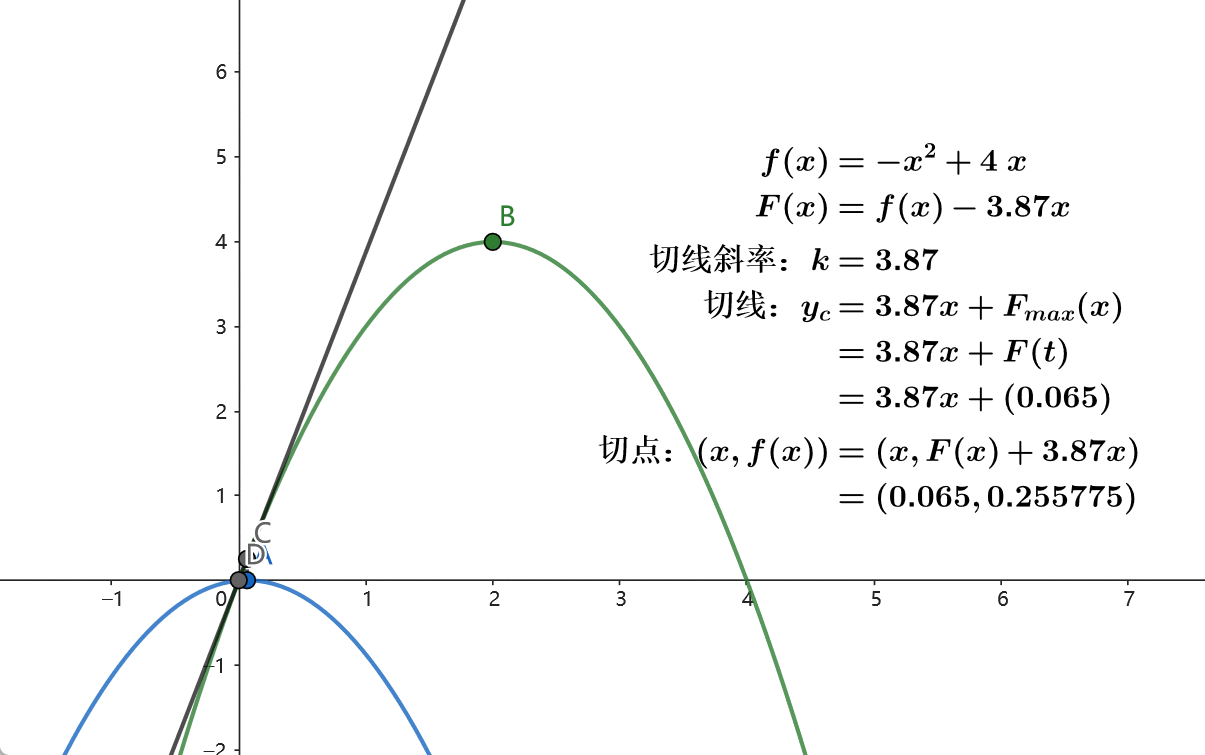
对于切线来说，不阐述概念，但是我们可以观察一下性质。

我们让一个固定斜率$k$的直线取切这个二次函数（也是个凸包）

发现什么？当恰好在切点时，截距$b$ 最大，这是条基本也是条很重要的性质。

3. 斜率优化

3.1 k与x同单调

来做DP题。

$n$ 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这$n$ 个任务被分成若干批，每批包含相邻的若干任务。
从零时刻开始，这些任务被分批加工，第$i$ 个任务单独完成所需的时间为$t_i$。在每批任务开始前，机器需要启动时间$s$，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。
每个任务的费用是它的完成时刻乘以一个费用系数$c_i$。请确定一个分组方案，使得总费用最小。
$1\le n \le 5000$，$0 \le s \le 50$，$1\le t_i,f_i \le 100$。

我们无论怎么分段和后面没有任何关系，每一个分段问题都是一个子问题且满足无后效性，我们其实没有必要单独设计分的段数这一状态来记录，不难设计转移方程：

$$f(i)=\min\limits_{j=1}^{i-1} f[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[n]-sumC[j])$$

• $f(i)$：表示把前$i$个任务分成若干批执行的最小费用。
• $sumT$：$t_i$的前缀和
• $sumC$：$c_i$的前缀和

其实这里有一个费用提前计算的思想，观察转移方程后面部分的$S*(sumC[n]-sumC[j])$。我们并不知道前面启动过几次及其，但是执行任务花费的启动时间$S$必定会对后面的计算造成影响，累加贡献。

显然时间复杂度$O(n^2)$，代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=5125;
int n,s;
ll a[MN],sumt[MN],sumc[MN],f[MN];
int main(){
    cin>>n>>s;
    for(int i=1;i<=n;i++){
        ll t,c;
        cin>>t>>c;
        sumt[i]=sumt[i-1]+t;
        sumc[i]=sumc[i-1]+c;
    }
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<i;j++){
            f[i]=min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));
        }
    }
    cout<<f[n];
    return 0;
}

但是我们如果要求时间复杂度$O(n)$呢？

我们观察以下这个式子，首先这个$\min$太难受了，反正我知道要取就行：

$$f(i)=f[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[n]-sumC[j])$$

我们拆一下这个式子，移个项。

$$\begin{aligned} f[i] & =f[j]+sumT[i]*sumC[i]-sumT[i]*sumC[j]+S*sumc[n]-S*sumc[j] \\ f[j] & = (S+sumT[i])*sumC[j]+f[i]-sumT[i]*sumC[i]-S*sumC[n] \end{aligned}$$

观察以下这个式子，首先$sumT[i],sumC[n],sumC[i],i,n$ 我们肯定都是知道的（外层循环$i$不变吗），但是其中唯一一个遍历$j$ 的我们不知道，我们观察这个式子。有没有发现什么？

我们不妨设$k=S+sumT[i],b=f[i]-sumT[i]*sumC[i]-S*sumC[n]$

原式就有：

$$f[j]=k*sumC[j]+b$$

这不是一次函数吗！

而且$k,b$我们肯定都是知道的，那么这个问题就变成一次函数的形式了，其图像是在以$sumC[j]$为横坐标$f[j]$为纵坐标的平面直角坐标系上。

根据我们开头提到的决策点，实际上每一个决策都对应坐标系的一个点$(sumC[j],f[j])$，每一个我想求解的$f[i]$一定对应这一个直线的截距。我们搬一下oiwiki的图。

这些黑点都是当前$f[i]$待选择的决策点。

我们的斜率$k$肯定是固定的，但是我们的$b$不一定。我们实际上就是在拿一条线从下去往上平移，并且要求我们的$b$最小（因为$b$里面有$f[i]$，我们要求$f[i]$的最小值），那么会靠到哪个点成为最优的呢？

我们连一下，发现了一个凸包，那么我们想想一条直线从下往上去平移。什么点会成为其决策呢？

不难发现就是凸包的切线！

所以我们可以通过构造像这样的“凸包”我们解可以快速找到这条切线使得截距$b$最小，但是有的时候并不是一个凸壳内所有点都能被切到，如蓝书上的图：

我们其实不难发现，要想获得最优决策，我们应当维护一个斜率单调递增的下凸壳，且顶点才能成为最优决策。

怎么求顶点，其实很简单？观察直线，最优决策点左边线斜率比$k$小，而右边大：

怎么维护？斜率单调递增，横坐标也肯定单调递增？比当前$k$小的会被排除不被选择…单调队列！

只需要维护一个单调队列，每一次新循环排除斜率$k'\le k$ 的决策，那么队列头即为顶点，即最优决策。

那么我们只需要这么维护：

1. 检查队头2个决策变量，若他们构成的斜率$k' \le k$，直接out！
2. 取队头计算$f[i]$
3. 插入决策点$i$，检查插入的时候队尾2个决策和$i$ 满不满足斜率单调递增，不满足就把$q[r]$ out了继续检查。

这样的时间复杂度就是$O(n)$

#include <bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN = 3e5+15;
int n, s;
ll a[MN], sumt[MN], sumc[MN], f[MN], q[MN];
int main()
{
    cin >> n >> s;
    for (int i = 1; i <= n; i++)
    {
        ll t, c;
        cin >> t >> c;
        sumt[i] = sumt[i - 1] + t;
        sumc[i] = sumc[i - 1] + c;
    }
    memset(f, 0x3f, sizeof(f));
    f[0] = 0;

    // O(n^2)
    // for(int i=1;i<=n;i++){
    //     for(int j=0;j<i;j++){
    //         f[i]=min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));
    //     }
    // }

    // O(n)
    int l = 1, r = 0;
    q[++r]=0;
    for (int i = 1; i <= n; i++)
    {
        ll k=s+sumt[i];
        while (l < r && (f[q[l + 1]] - f[q[l]]) <= k * (sumc[q[l + 1]] - sumc[q[l]]))
        {
            // 除法转乘法避免小数
            l++;
        }
        f[i] = f[q[l]] - k * sumc[q[l]] + sumt[i] * sumc[i] + s * sumc[n];
        while (l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]]) >= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]]))
            r--;
        // 分式交叉相乘避免小数
        q[++r] = i;
    }
    cout << f[n];
    return 0;
}

坑点解析：

1. 为什么单调队列循环中是$l<r$，因为你判断斜率至少要2个决策点才能判断。
2. 单调队列需在其中至少插入一个元素，默认为0
3. 可以不用乘法，除法注意精度（long double）

这道题也是做完了。

总结一下，我们和单调队列优化相比，我们这里的单调性依赖的是元素的比值，因为这个对应斜率，我们称之为斜率优化。

3.2 k不单调，x单调

什么意思，就是斜率不再单调了但是横坐标还是单调递增，那么不能像之前这样贸然的取队头了，我们无法从上一轮的最优点开始，直接往后在凸壳上找到这一轮的最优点。也就是说，必须搜索当前的整个凸壳！

作者：しずり雪博客的图

但其实维护凸壳的时候斜率函数单调递增，我们可以借助这个二分，找到顶点就可以了，其实二分也可以套在$k$ 与$x$ 同单调的地方，芝士没有那么优罢了。

时间复杂度显然$O(n\log n)$

例题：

同上题，但：$1 \le n \le 3 \times 10^5$，$1 \le s \le 2^8$，$\left| T_i \right| \le 2^8$，$0 \le C_i \le 2^8$。

$sumT$有可能是负数，不再单调递增，所以考虑二分。

代码如下：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN = 3e5+15;
int n, s,l,r;
ll a[MN], sumt[MN], sumc[MN], f[MN], q[MN];

ll binsearch(ll k){
    if(l==r) return q[l];
    int L=l,R=r;
    while (L<R)
    {
        int mid=L+R>>1;
        //
        if(f[q[mid+1]]-f[q[mid]]>k*(sumc[q[mid+1]]-sumc[q[mid]])) R=mid;
        else L=mid+1;
    }
    return L;
}

int main()
{
    cin >> n >> s;
    for (int i = 1; i <= n; i++)
    {
        ll t, c;
        cin >> t >> c;
        sumt[i] = sumt[i - 1] + t;
        sumc[i] = sumc[i - 1] + c;
    }
    memset(f, 0x3f, sizeof(f));
    f[0] = 0;

    // O(n^2)
    // for(int i=1;i<=n;i++){
    //     for(int j=0;j<i;j++){
    //         f[i]=min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));
    //     }
    // }

    l=1,r=0;
    q[++r]=0;
    // O(n) 没有维护下凸包只有上凸包
    // for (int i = 1; i <= n; i++)
    // {
    //     ll k=s+sumt[i];
    //     //为什么这里是l<r? l<r 能保证队列中至少有2个数，我们比较斜率是 delta(y)/delta(x) 2个值凑delta
    //     while (l < r && (f[q[l + 1]] - f[q[l]]) <= k * (sumc[q[l + 1]] - sumc[q[l]]))
    //     {
    //         // 除法转乘法避免小数
    //         l++;
    //     }
    //     f[i] = f[q[l]] - k * sumc[q[l]] + sumt[i] * sumc[i] + s * sumc[n];
    //     while (l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]]) >= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]]))
    //         r--;
    //     // 分式交叉相乘避免小数
    //     q[++r] = i;
    // }

    // O(nlogn) 维护下凸包与上凸包，因为sumt不再具有单调性，不再是只有上凸包还有下凸包
    // 还是考虑维护单调递增的k，不过这次我们要二分查找了因为队首不再是最优决策了

    for(int i=1;i<=n;i++){
        ll k=s+sumt[i];
        ll p=binsearch(k);
        f[i] = f[q[p]] - k * sumc[q[p]] + sumt[i] * sumc[i] + s * sumc[n];
        while (l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]]) >= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]]))
            r--;
        q[++r]=i;
    }

    cout << f[n];
    return 0;
}

3.3 k单调x不单调

也就是$k$还有单调性，但是$x$没有单调性。这个时候可能在任意一个点插，我们需要动态维护凸包。

• k：对于斜率因为还是有单调性，我们可以像3.2一样直接二分
• x：我们不能用单调队列来优化了，必须出动高级算法：
  • 李超线段树 时间复杂度$O(n\log n)$
  • CDQ分治$O(n\log n)$
  • set维护$O(n\log n)$

选择你喜欢的英雄，反正我选了李超www。

来做题：P4655

有$n$ 根柱子依次排列，每根柱子都有一个高度。第$i$ 根柱子的高度为$h_i$。
现在想要建造若干座桥，如果一座桥架在第$i$ 根柱子和第$j$ 根柱子之间，那么需要$(h_i-h_j)^2$​​ 的代价。
在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第$i$ 根柱子被拆除的代价为$w_i$，注意$w_i$ 不一定非负，因为可能政府希望拆除某些柱子。
现在政府想要知道，通过桥梁把第$1$ 根柱子和第$n$ 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

不难有转移方程：

$$f[i]=\min\limits_{j=1}^{i-1} f[j]+h_{i^2}-2h_ih_j+h_J^2+s_{i-1}-s_j$$

其中$s$ 为$w$的前缀和。

式子化简有：

$$f[i]=h_i^2+s_{i-1}+\min({f[j]-2h_ih_j+h_j^2-s_j})$$

显然斜率肯定递增，但是$h$不一定，我们考虑李超，李超的作用是什么？多条线段单点最值，我们的单点的$x$是必须固定。

令$k=-2h_j,b=f_j+h_J^2-s_j$

有$$f[i]=h_i^2+s_{i-1}+min(k*h_i+b)$$
李超即可。

#include<bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
using namespace std;
const ll MN=1e6+15,INF=1e18,M=1e6;
struct line{
    ll k,b;
}ln[MN];
struct node{
    int l,r,id;
}t[MN<<2];
ll f[MN],h[MN],s[MN];
int n;

ll clac(int id,int x){
    return ln[id].k*x+ln[id].b;
}


void build(int p,int l,int r){
    t[p].l=l;
    t[p].r=r;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(ls,l,mid);
    build(rs,mid+1,r);
}

void update(int p,int i){
        if(t[p].l==t[p].r){
            if(clac(i,t[p].l)<clac(t[p].id,t[p].l)) t[p].id=i;
            return;
        }
        int mid=(t[p].l+t[p].r)>>1;
        if(clac(i,mid)<clac(t[p].id,mid)){
            swap(i,t[p].id);
        }
        if(clac(i,t[p].l)<clac(t[p].id,t[p].l)){
            update(ls,i);
        }
        if(clac(i,t[p].r)<clac(t[p].id,t[p].r)){
            update(rs,i);
        }
        return;
}

ll query(int p,ll k){
    ll ret=INF;
    if(t[p].id) ret=clac(t[p].id,k);
    if(t[p].l==t[p].r) return ret;
    int mid=(t[p].l+t[p].r)>>1;
    if(mid>=k) ret=min(ret,query(ls,k));
    else ret=min(ret,query(rs,k));
    return ret;
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>h[i];
    }
    for(int i=1;i<=n;i++){
        cin>>s[i];
        s[i]+=s[i-1];
    }
    ln[0].b=INF;
    build(1,0,M);
    ln[1].k=-2*h[1];
    ln[1].b=h[1]*h[1]-s[1];
    update(1,1);
    for(int i=2;i<=n;i++){
        f[i]=query(1,h[i])+s[i-1]+h[i]*h[i];
        ln[i].k=-2*h[i];
        ln[i].b=f[i]-s[i]+h[i]*h[i];
        update(1,i);
    }
    cout<<f[n];
    return 0;
}

3.4 k不单调，x不单调

其实和3.3差不太多。

3.5 补充例题

矩阵优化+斜率优化 CF1067D

首先这个升级显然是吓唬你的，因为我可以一直选一个游戏 van，所以我只需要看$b_{i}p_{i}$ 最大就可以了。但是这里我们并不能考虑贪心，因为在时间短的情况下可能升级升不了，还是要 dp 的。

不难有 dp 方程如下，设$f(t)$ 表示还剩下$t$ 秒的最大期望，$v$ 表示$b_{i}p_i$ 的最大值：

$$f(t+1)= \max_{i=1}^n \left\{ \underbrace{p_{i}(tv+a_i)}_{\text{升级成功}} + \underbrace{（1-p_{i})f_t}_{\text{升级失败}} \right\}$$

时间复杂度$O(nt)$ ，这太$nt$ 了www
不难看出来可以斜率优化啊，但是我们要变下形式：

$$\begin{aligned} f(t+1) & = \max_{i=1}^n \left\{ p_{i}(tv+a_i) + (1-p_{i})f_t \right\} \\ & = p_{i}tv+p_{i}a_{i}+f_t-p_{i}f_{t} \\ & = p_{i}(tv-f_t)+p_{i}a_{i}+f_t \end{aligned}$$

因为$f_{t}$ 是已知的，所以这个就是一个显然的斜率优化式子，通过将$p_i$ 排序可以满足$k$ 单调，但是$x$ 呢？其实也是一样的：

$$\begin{aligned} tv-f_{t}& \ge (t-1)v-f_{t-1} \\ tv-f_{t}& \ge tv-v-f_{t-1} \\ f_{t-1}-f_{t} & \le v \end{aligned}$$

因为两个游戏之间获得的收益不可能比玩最大收益（最大的$b_{i}p_{i}$ 的游戏）还大，所以式子成立，$x$ 单调不降。

故单调队列优化，时间复杂度$O(t+n)$…$t\le 10^{10}$？

这个数据范围已经不行了，必须出矩阵优化…等会矩阵怎么斜率优化？

首先我们先把转移的矩阵搞出来，推啊推：

$$\begin{bmatrix} f_{i-1} & i-1 & 1 \end{bmatrix} \times \begin{bmatrix} (1-p_i) & 0 & 0\\ p_i v & 1 & 0\\ (p_i-a_i) & 1 & 1 \end{bmatrix} = \begin{bmatrix} f_{i} & i & 1 \end{bmatrix}$$

其实也不是很难推，有啥加啥，因为少个 1 直接加上去就行。

如果我们想找出来有哪些游戏是我们在斜率优化需要的，可以利用单调栈（不能用单调队列我们要存下来的）来记录我们斜率从那些点转移过来，现在问题在于如何确定什么时候从一个点转移到另一个点。

回忆一下这张图：

在斜率优化上，我们能用单调队列来做是因为对于每一个点上的斜率，它有一定转移的边界，在这之前是这个斜率，在之后就不是了。

说的好听矩阵怎么做？首先一个游戏的转移矩阵肯定不会变。问题在于我们怎么像单调队列优化一样找到所谓的边界呢？

首先单调队列不太行因为它不适用于矩阵这种玩意，那怎么办，矩阵这玩意也不能上不单调三小将…………二分？

但其实维护凸壳的时候斜率函数单调递增，我们可以借助这个二分，找到顶点就可以了，其实二分也可以套在$k$ 与$x$ 同单调的地方，芝士没有那么优罢了 —— 3.2 k不单调 x单调

我们可以二分矩阵快速幂的幂，到哪个幂的时候转移是最优的！这样的时间复杂度是$O(n \log^2 t)$，可以通过。

我们不妨快点，不难发现幂其实是一个倍增的形式，我们可以利用倍增的形式二分，首先预处理矩阵快速幂后的各个幂对应的矩阵，从大到小枚举倍增的幂，不断检查是否合法（即是否$<t$ )，让后检查是否更优，直接赋值即可！时间复杂度$O(n \log t)$，其中$\log t=33$ 可以通过。

代码如下，注意精度！！！！！：

#include<bits/stdc++.h>
#define ll long long
#define double long double
using namespace std;
constexpr int MN=6e5+15;
constexpr double eps=1e-13;
struct Node{
    double k,b;
}ln[MN],cl[MN],s[MN];
ll n,t,top,tot,now;
double v;

struct Matrix{
    double mat[5][5];

    Matrix operator *(const Matrix &x)const{
        Matrix ret;
        memset(ret.mat,0,sizeof(ret.mat));
        for(int i=1;i<=3;i++){
            for(int j=1;j<=3;j++){
                for(int k=1;k<=3;k++){
                    ret.mat[i][j]+=mat[i][k]*x.mat[k][j];
                }
            }
        }
        return ret;
    }

}g[40],f;

bool cmp(Node x,Node y){
    if(fabs(x.k-y.k)<eps) return x.b<y.b;
    return x.k<y.k;
}

int ck(double x){
    if(fabs(x)<eps) return 0;
    return x>0?1:-1;
}

double gety(Node x,Node y){
    return (x.b-y.b)/(y.k-x.k);
}

int main(){
    cin>>n>>t;
    for(int i=1;i<=n;i++){
        double a,b,p;
        cin>>a>>b>>p;
        v=max(v,b*p);
        ln[i].k=p;
        ln[i].b=p*a;
    }
    sort(ln+1,ln+1+n,cmp);
    for(int i=1;i<=n;i++){
	    // 先把那些相等斜率的全排了
        if(i == n || ck(ln[i].k - ln[i+1].k) != 0) cl[++tot]=ln[i];
    }
    for(int i=1;i<=tot;i++){
	    // 单调栈处理转移的点
        while(top>1&&ck(gety(s[top],s[top-1])-gety(cl[i],s[top-1]))>=0) top--;
        s[++top]=cl[i];
    }
    // f 为 初始矩阵
    f.mat[1][3]=1;
    for(int i=1;i<=top;i++){
        double x=now*v-f.mat[1][1];
        while(i<top&&ck(x-gety(s[i],s[i+1]))>=0) i++;// 先把过时决策排了
        if(i<top) x=gety(s[i],s[i+1]);
        g[0].mat[1][2]=g[0].mat[1][3]=g[0].mat[2][3]=0;
        g[0].mat[2][2]=g[0].mat[3][2]=g[0].mat[3][3]=1;
        g[0].mat[1][1]=1-s[i].k,g[0].mat[2][1]=s[i].k*v,g[0].mat[3][1]=s[i].b;// 初始化矩阵
        for(int j=1;j<=35;j++) g[j]=g[j-1]*g[j-1];
        for(int j=35;j>=0;j--){
            ll np=now+(1ll<<j);
            if(np>=t) continue;
            // 如果决策更优或已经到头了即可转移
            if(i==top||ck(x-np*v+(f*g[j]).mat[1][1])>=0){
                f=f*g[j];
                now=np;
            }
        }
        f=f*g[0];
        now++;
        if(now==t) break;
    }
    cout<<fixed<<setprecision(10)<<f.mat[1][1];
    return 0;
}

3.6 总结

对于求最小值，应当维护下凸包，而最大值维护上凸包。

特征方程：$f[i]=\min_{j=1}^{i-1} f[j]-a[i]d[j]$

特点存在既有$i$又有$j$的项$a[i]d[j]$,并且两项均单调不减。

主要尝试把式子化成一个$y=kx+b$的形式，有的时候$b$可能会带高次项，不要怕当成整体看就可以了。

4.WQS带权二分

特征：$f(i,j)=min/max(g(i,k)+w(i,j))\,,\,j\in[1,i],w(i,j)$无明显性质。
当$i$固定时，$f(i,j)$为凸函数。

当不限定$j$时，$f(i)$能够$O(n)$计算。

例题：

给定$n$个物品，每个物品有价值$w$（$w$可以小于0），从中选$m$个物品求最大价值。

这不是背包吗？但是我要求你$O(n\log n)$呢？

一个简单的思路是$w_i$排序，但是简单地排序无法保证正确性。

有朴素转移方程,时间复杂度$O(n^2)$：

$$f(i,j)=\max\limits_{j=1}^i (f(i-1,j),f(i,j-1)+w(i))$$

解题思路：

1. 检查f(k,j)关于j的凸性

既然优化，我们需要挖掘性质来进行优化。

这里的f(k,j)关于j的凸性是什么意思呢，实际上就是我们固定$f(i,j)$其中的$i=k$，根据$j$的变化我们来看满足什么性质。

显然为上凸函数，因为我少选还不如多选吗，我选的越多肯定我拿到的钱就最多吗。

2. 不限制 j 的时候f(i)很好算

如果不限制的化，那么很简单。

$$f(i)=\max (f(i-1),f(i-1)+w_i)$$

时间复杂度$O(n)$，目标$f(n)$。

如果$f(n)$代表的刚好就是选$m$个物品时的最大价值，那不就可以了吗。

萧苯单，谁跟你说一定是$m$个了，往上看看题目后面对于$w$说的什么，$w_i$可能为负数，不限制取那么肯定不选负数价值的。那怎么办？

3. 直线切点求截距

还是一张图(实际上你是求不出来点的大致画一下就可以了），这里$f(x)$与$g(x)$是相同的：

我们用一条直线$y=kx+b$去切一个点$(x,g(x))$，显然有$g(x)=kx+b$，那么这个点可以表示为$(x,kx+b)$。

因为凸包有个性质，我们和这个凸包的顶点相切那么截距$b$肯定最大，这个在斜率优化里面提到过，假设我们知道$k$，只要我们求出最大的$b$并知道顶点$x$，就能确定具体坐标$g(x)$了。不难发现和斜率优化类似的一点是$k$具有单调性，所以我们只需要去二分$k$，就可以了。

问题在于怎么求最大截距$b_{max}$?

这个凸包我们根本都不知道长啥，如果先求出来那复杂度肯定会爆炸。

不难发现$b=g(i)-kx$，考虑再重新设转移方程，设$h(i)$表示当前$g(i)$的最大截距。显然有$h(i)=g(i)-kx$。我们求$h_i$并没有规定非要选多少个，而且不难发现$h(i)$是可以DP出来的，并且只是源问题的转换：

给定$n$个物品，每个物品有价值$w$（$w$可以小于0），同时选择物品会带有$k$的负权值，任意选择求最大价值。

不难有转移方程：

$$h(i)=\max (h(i-1),h(i-1)+w(i)-k)$$

每个都减去$k$其实就是$kx$，解释以下。

问题在于如果这么搞的这$h(i)$还是个凸函数吗，我们还想要他的极值点呢。

显然是的，可以看看下面的图，利用二次函数来模拟：

不难发现其实还是凸函数

那么用他的最值点来求$f(i,j)$，求$h(x)$显然为$O(n)$，转化为$O(1)$。

但是还是有一个问题，我怎么知道它能够恰好选到$m$个物品呢？这个时候$-k$的作用就体现在这里了，我们每选取一个物品，额外减少$k$的价值，间接限制DP对物品的选取数量，如下图：

并且不难发现一个性质，他的极值点随$k$增大而减少，这是因为$f$的凸性造成的。

我们可以在一定范围内对$k$进行二分，直到找到某个$h_k(n)$的极大值点刚好对应选$m$个物品，这样我们就获得了$f(n,m)$的值，二分时间复杂度$O(\log n)$，一次DP求最大$b$时间复杂度$O(n)$，时间复杂度$O(n\log n)$。我们搜索范围最大为$[0,max(w(i))]$。如果斜率存在小数我们需要实数二分，反之整数二分。

特别注意！

如果是总代价最小化，我们需要加上$k$的代价。
如果是总代价最大化，我们需要减去$k$的代价。
这其实很好理解可以画画图，下凸壳和上凸壳的维护是不同的。

你的整数二分要和$h_k$的计算要匹配，如果$h$出现多点共线，整数二分只能获取到左右端点，搜索出来的选取个数不一定为$m$，但是可以算中间的点因为获得$h$是一样的，只是加上的$kx$不同。

如图：

注意有没有可能$m$永远无法取到，如果$t<m,m<t$任意一个成立，其中$t$为极致点选取的物品个数，那么$m$对应的$h(n,m)$百分百与$h(n,t)$（这里加上第二维是指极致点共选了多少个，不是状态中原本就有这个）共线，所以需要特别考虑。

WQS模板题

P6246 [IOI 2000] 邮局

高速公路旁边有$n$ 个村庄。高速公路表示为整数轴，每个村庄的位置用单个整数坐标标识。两个位置之间的距离是其整数坐标差的绝对值。
现在要建立$m$ 个邮局，邮局将建在一些，但不一定是所有的村庄中。为了建立邮局，应选择他们建造的位置，使每个村庄与其最近的邮局之间的距离总和最小。
你要编写一个程序，已知村庄的位置和邮局的数量，计算每个村庄和最近的邮局之间所有距离的最小可能的总和。

邮局肯定放在一个区间的中间（中位数？），那么显然有朴素状态转移方程：设$f(i,j)$表示到了第$i$个村庄，共放了$j$个邮局，有：

$$f(i,j)=\min\limits_{j=1}^{i-1}f(j,i-1)+dis(j,i)$$

有人会问不是可以不放吗，你不放距离肯定大啊不是最优解，这里埋个铺垫后面会提到。

不难发现$dis$其实可以$O(n^2)$预处理。

DP3维枚举时间复杂度$O(n^3)$

考虑优化，不难发现$dis$满足四边形不等式，可以优化到$O(n^2\log n)$，进一步可以优化到$O(n^2)$。这个复杂度还是不好，不能满足我们对于NOI的胃口。

“有人会问不是可以不放吗，你不放距离肯定大啊不是最优解”，这句话说明什么？

$f(i,j)$有凸性！而且还是刚好$m$个邮局，和上面我们提到的问题是一样的，不难推出$h(i)$的图像其实是一个下凸壳，不难发现$h(i)$还可以继续用四边形不等式优化，复杂度$O(n\log n)$。故时间复杂度为$O(n \log n \log |V|)$，其中$V$为值域。

很难发现$dis$可以$O(1)$计算。怎么算看题解把（雾）

#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=5e5+15;
struct queueueue{
    int l,r,j;
}q[MN];
int n,m,ql,qr;
ll pos[MN],sump[MN],ans[MN];
ll f[MN];

ll w(int l,int r){
    int p=(l+r+1)>>1;
    return (sump[r]-sump[p])-(ll)pos[p]*(r-p)+(ll)pos[p]*(p-l)-(sump[p]-sump[l]);
}

void insert(int x){
    int pos=n+1;
    while(ql<=qr&&f[x]+w(x,q[qr].l)<=f[q[qr].j]+w(q[qr].j,q[qr].l)) pos=q[qr--].l;
    if(ql<=qr&&f[x]+w(x,q[qr].r)<=f[q[qr].j]+w(q[qr].j,q[qr].r)){
        int l=q[qr].l,r=q[qr].r;
        while(l+1<r){
            int mid=(l+r)>>1;
            if(f[x]+w(x,mid)<=f[q[qr].j]+w(q[qr].j,mid)) r=mid;
            else l=mid;
        }
        q[qr].r=r-1;
        pos=r;
    }
    if(pos!=n+1){
        q[++qr]={pos,n,x};
    }
}

bool check(ll k){
    ql=1,qr=0;
    q[++qr]={1,n,0};
    for(int i=1;i<=n;i++){
        while(ql<=qr&&q[ql].r<i) ql++;
        f[i]=f[q[ql].j]+w(q[ql].j,i)+k;
        ans[i]=ans[q[ql].j]+1;
        insert(i);// 可以看蓝书的四边形不等式教程，照这写的
    }
    // cout<<ans[n]<<" ";
    return ans[n]>=m;//我们需要>=m的决策
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>pos[i];
    }
    sort(pos+1,pos+1+n);
    for(int i=1;i<=n;i++){
        sump[i]=sump[i-1]+pos[i];
    }
    ll l=0,r=8e11;
    while(l+1<r){
        ll mid=(l+r)>>1;
        if(check(mid)) l=mid;
        else r=mid;
    }
    check(l);
    cout<<f[n]-m*l;// 减去kx
    return 0;
}

CF739E Gosha is hunting

你要抓神奇宝贝！ 现在一共有 $n$ 只神奇宝贝。 你有 $a$ 个『宝贝球』和 $b$ 个『超级球』。 『宝贝球』抓到第 $i$$只神奇宝贝的概率是$p_i$​，『超级球』抓到的概率则是$u_i$​。 不能往同一只神奇宝贝上使用超过一个同种的『球』，但是可以往同一只上既使用『宝贝球』又使用『超级球』（都抓到算一个）。 请合理分配每个球抓谁，使得你抓到神奇宝贝的总个数期望最大，并输出这个值，注意概率为实数。$1\le n\le 2000$

期望DP，我们先列个小方程出来。设$f(i,j,k)$表示第$i$只神奇宝贝，总共用了$j$个宝贝球与$k$个超级球，显然有：

$$f(i,j,k)=\max \begin{cases} f(i-1,j,k) & \text{不选} \\ f(i-1,j-1,k)+P_i & \text{用宝贝球} \\ f(i-1,j,k-1)+U_i & \text{用超级球} \\ f(i-1,j-1,k-1)+1-(1-P_i)(1-U_i) & \text{都用} \end{cases}$$

不难发现还是有凸性的，但是有两个限制变量，怎么办？那就WQS二分套WQS二分！

$$f(i)=\max \begin{cases} f(i-1) & \text{不选} \\ f(i-1)+P_i-k_a & \text{宝贝球} \\ f(i-1)+U_i-k_b & \text{超级球} \\ f(i-1)+P_i+U_i-P_iU_i-k_a-k_b & \text{都用} \end{cases}$$

本题有实数二分，注意精度问题，并且要滚动数组一下不然会炸空间。

#include<bits/stdc++.h>
#define pir pair<double,double>
using namespace std;
constexpr int MN=2501;
constexpr double eps=1e-8;
double p[MN],q[MN];
double f,pref;
int n,a,b;

pir check(double ka,double kb){
    pref=0;
    int cnta=0,cntb=0;
    for(int i=1;i<=n;i++){
        //pref即f[i-1]
        f=max({pref,pref+p[i]-ka,pref+q[i]-kb,pref+p[i]+q[i]-p[i]*q[i]-ka-kb});
        if(f-(pref+p[i]-ka)<eps){
            cnta++;
        }else if(f-(pref+q[i]-kb)<eps) cntb++;
        else if(f-(pref+p[i]+q[i]-p[i]*q[i]-ka-kb)<eps){
            cnta++;
            cntb++;
        }
        pref=f;
    }
    return pir(cnta,cntb);
}

int main(){
    cin>>n>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>p[i];
    }
    for(int i=1;i<=n;i++){
        cin>>q[i];
    }
    double la=0,ra=1,lb,rb,mida,midb;
    while(la+eps<ra){//先a
        mida=(la+ra)/2;
        lb=0,rb=1;
        pir ansb;
        while(lb+eps<rb){// 后b
            midb=(lb+rb)/2;
            ansb=check(mida,midb);
            if(ansb.second>b) lb=midb;
            else if(ansb.second<b)rb=midb;
            else break;//如果找到了就退出
        }
        if(ansb.first>a) la=mida;
        else if(ansb.first<a)ra=mida;
        else break;
    }
    cout<<f+mida*a+midb*b;//因为我们取最小，h(i)是减去k，这里要加上
    return 0;
}

UVA1537 Picnic Planning

给定一张 n 个点 n 条边的无向图，正边权，求出无向图的一棵最小生成树，满足一号节点的度数不超过给定的整数 s.
$n\le 20$

这不对啊这个和DP有什么关系？这不是显然有后效性吗。而且这题正解什么时候是WQS了。

事实上WQS二分可以套在许多类型的题上，不仅仅局限于DP.(只是没打标签而已)

观察这个题，又是我们熟悉的强迫$s$，要求最小值。

考虑在不限制$s$ 的情况下显然变为最小生成树模板可以$O(m \log m)$做。

观察当我们选择加入最小生成树，连一号节点的边数越多，总边权越来越大（正边权），显然是个凸函数，考虑WQS二分消去$s$的限制。

首先我们计算时需要统计一号节点的度数$cnt$，如果$cnt\le S$，显然不用算。反之，进行WQS二分。

我们的权值$k$加的情况，当且仅当边连的是一号节点我们才加上权值。在排序的时候记得要加上特判。

时间复杂度多少？一次kru显然$O(m\log m)$，总时间复杂度显然为$O(Tm\log m \log |V|)$，其中$V$为值域。

故代码如下：

#include<bits/stdc++.h>
#define getid(x) (!ump[x]?ump[x]=++umptot:ump[x])
#define pir pair<int,int>
using namespace std;
constexpr int MN=1314;
struct Edge{
    int u,v,w;
}e[MN];
int pre[MN],n,k,T,umptot,s;
unordered_map<string,int> ump;

int root(int x){
    if(pre[x]==x) return pre[x];
    else return pre[x]=root(pre[x]);
}

void initpre(){
    for(int i=1;i<=umptot;i++){
        pre[i]=i;
    }
}

bool cmp(Edge x,Edge y){
    if(x.w+k*(x.u==1)==y.w+k*(y.u==1)) return x.u!=1;
    return x.w+k*(x.u==1)<y.w+k*(y.u==1);
}

pir kru(){
    int ans=0,cnt=0;
    initpre();
    sort(e+1,e+1+n,cmp);
    for(int i=1;i<=n;i++){
        int ru=root(e[i].u),rv=root(e[i].v);
        if(ru==rv) continue;
        pre[rv]=ru;
        ans+=e[i].w;
        if(e[i].u==1){
            cnt++;
            ans+=k;
        }
    }
    //cout<<"K:"<<k<<" "<<ans<<" "<<cnt<<'\n';
    return pir(ans,cnt);
}

void solve(){
    ump.clear();
    umptot=1;
    ump["Park"]=1;
    cin>>n;
    for(int i=1;i<=n;i++){
        string u,v;
        int w;
        cin>>u>>v>>w;
        e[i].u=getid(u);
        e[i].v=getid(v);
        e[i].w=w;
        
        if(e[i].u>e[i].v) swap(e[i].u,e[i].v);
        //cout<<e[i].u<<" "<<e[i].v<<" "<<e[i].w<<'\n';
    }
    cin>>s;
    int l=0,r=1000;
    k=0;
    if(kru().second<=s){
        cout<<"Total miles driven: "<<kru().first<<'\n';
        if(T) cout<<'\n';
        return;
    }
    //cout<<umptot<<'\n';
    while(l+1<r){
        int mid=(l+r)>>1;
        k=mid;
        if(kru().second>s) l=mid;
        else r=mid;
    }
    k=r;
    cout<<"Total miles driven: "<<kru().first-s*k<<'\n';
    if(T) cout<<'\n';
}

int main(){
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

WQS总结

主要是利用凸包这一特性来消除掉选$m$的特性，适用的问题一般是$n$个里面强制选$m$个的问题，求最大最小价值，并且如果可以随便选可以很简单的做的题。最难的是发现性质。

主要注意二分斜率时的细节。

写在最后

感谢阅读！

本文章素材来源：

1. 算法竞赛进阶指南
2. FloatingLife的WQS二分博客,链接
3. しずり雪 の Blog

本文章遵循开源协议——[知识共享署名-相同方式共享 4.0 国际许可协议]。