注:线性代数并不算于这篇文章
数论应该算是oi里面一个比较算是重要的章节了吧,他在大纲内标得难度居然比平衡树还简单?听老师说这个难度其实是按学起来的难度表的。应用起来和平衡树的区间操作一样难。
故借一个下午,整理数论笔记,重新思考思考一下吧。
数论研究的是整数的性质,但是性质要好多啊啊啊。一个一个慢慢学吧.
整除应该早就在小学中学过他的概念了。这里我们添加几个符号来表示整除,并且重新复述一遍定义。
若a a a b b b a a a b b b b是a的倍数,a是b的约数(或者也可以叫做因数) ,我们记为a ∣ b a|b a ∣ b
若a ∣ b a|b a ∣ b m m m a m ∣ b m am|bm a m ∣ b m
若a ∣ b a|b a ∣ b b ∣ c b|c b ∣ c a ∣ c a|c a ∣ c
若a ∣ b c a|bc a ∣ b c a a a c c c a ∣ b a|b a ∣ b
若c ∣ a c|a c ∣ a c ∣ b c|b c ∣ b m , n m,n m , n c ∣ ( m a + n b ) c|(ma+nb) c ∣ ( m a + n b )
素数又称质数,其满足性质就是大于等于2,并且除了1和他本身外不能被其他的任何自然数整除。
不满足该性质的数为合数,但是1既不是素数又不是合数
2是唯一的偶素数
随着整数的增大,素数的分布越来越稀疏。随机整数x x x 1 l o g 2 x \frac{1}{log_2x} l o g 2 x 1
怎样取判定一个数是否为素数?我们先从定义来看,素数表示只能被1和自己整除的正整数。那我们就可以得到如下的做法
朴素判定:对n n n [ 2 , n ) [2,n) [ 2 , n ) n n n n n n O ( n ) O(n) O ( n ) 我们考虑一下优化,假设一个数能够整除n n n a ∣ n a|n a ∣ n n a \frac{n}{a} a n a a a a ≤ n a a\le \frac{n}{a} a ≤ a n a 2 ≤ n a^2\le n a 2 ≤ n a ≤ n a\le \sqrt{n} a ≤ n n \sqrt{n} n n \sqrt{n} n
优化判定:对n n n [ 2 , n ] [2,\sqrt{n}] [ 2 , n ] O ( n ) O(\sqrt{n}) O ( n ) 要不要再快点?我们显然可得如果n是合数,那么必然有一个小于等于n \sqrt{n} n n \sqrt{n} n s s s O ( s ) O(s) O ( s )
不过,我们发现这个的复杂度只能在1 0 12 10^{12} 1 0 1 2
给定n n n [ 2 , n ] [2,n] [ 2 , n ]
像上面一样逐个判断会很慢,我们可以用“筛子”,来一起筛所有的整数,把合数都筛掉。常用的两种算法分别为埃式筛和欧拉筛。
我们直接利用素数的定义,即除了1和他本身外不能被其他的任何自然数整除。可以得出他的倍数都是合数。
步骤如下
用一个标记数组f [ m a x n ] f[maxn] f [ m a x n ] f [ i ] = 0 f[i]=0 f [ i ] = 0 i i i f [ 0 ] = f [ 1 ] = 1 f[0]=f[1]=1 f [ 0 ] = f [ 1 ] = 1
从未被标记的数中找到最小的数,为2,它不是任何(除1与其本身)数的倍数,所以2是素数,这时候我们将4,6,8,10,…等2的倍数标记为1
从未被标记的数中找到最小的数,为3.它也是素数,我们把它的倍数也标记上,6,9,12…
从未被标记的数中找到最小的数,为5,它也是素数,我们标记他的倍数,10,15,20,25…
…
这种方式我们遍历完标记数组f [ i ] f[i] f [ i ] O ( n l o g l o g n ) O(nloglogn) O ( n l o g l o g n )
如果我们对于f f f v e c t o r < b o o l > vector<bool> v e c t o r < b o o l > b i t s e t bitset b i t s e t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 vector<int > prime; vector<bool > notprime (100000000 ) ;void aishi (int n) for (int i=2 ;i<=n;i++){ if (notprime[i]!=1 ){ prime.push_back (i); for (int j=i*2 ;j<=n;j+=i){ notprime[j]=1 ; } } } }
但是带log,当数量级增大的时候就会TLE。我们考虑上面的情况(重复划掉),我们发现有重复的数组被筛掉,我们能否优化掉这一过程呢
原理就是一个合数肯定有一个最小质因数。让每个合数被他的最小质因数筛选一次,以达到不重复筛的目的,步骤如下
逐一检查[ 2 , n ) [2,n) [ 2 , n )
当检查到第i i i x x x x x x
代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 vector<bool > notprime (MN+5 ) ;vector<int > prime; void shai () for (int i=2 ;i<=n;i++){ if (!notprime[i]){ prime.push_back (i); } for (int j=0 ;j<prime.size ();j++){ if (i*prime[j]>n) break ; notprime[i*prime[j]]=1 ; if (i%prime[j]==0 ){ break ; } } } }
我们可以比较一下埃式筛和线性筛的性能差距,都使用了vector优化
线性筛
埃式筛
飞快
我们来看素数真正的定义,也就是算数基本引理
设p p p p ∣ a 1 a 2 p|a_1 a_2 p ∣ a 1 a 2 p ∣ a 1 p|a_1 p ∣ a 1 p ∣ a 2 p|a_2 p ∣ a 2 算数唯一分解定理表示如下
设正整数a a a
n = p 1 p 2 p 3 . . . p k n=p_1p_2p_3...p_k n = p 1 p 2 p 3 . . . p k p 1 ≤ p 2 ≤ p 3 ≤ . . . ≤ p k p_1\le p_2\le p_3\le...\le p_k p 1 ≤ p 2 ≤ p 3 ≤ . . . ≤ p k
n = p 1 e 1 p 2 e 2 . . . p k e k n=p^{e_1}_{1}p^{e_2}_{2}...p^{e_k}_{k} n = p 1 e 1 p 2 e 2 . . . p k e k
遇到一个数不要只把它当作一个普普通通的数,要想到算数唯一分解定理。
还是靠经典的试除法,考虑朴素算法,因数是成对分布的,[ 2 , n ] [2,\sqrt{n}] [ 2 , n ] [ n + 1 , n ] [\sqrt{n}+1,n] [ n + 1 , n ] [ 2 , n ] [2,\sqrt{n}] [ 2 , n ] O ( n ) O(\sqrt{n}) O ( n )
代码如下(粘贴自oiwiki)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 vector<int > breakdown (int N) { vector<int > result; for (int i = 2 ; i * i <= N; i++) { if (N % i == 0 ) { while (N % i == 0 ) N /= i; result.push_back (i); } } if (N != 1 ) { result.push_back (N); } return result; }
证明result中所有元素是N N N
还是试除法,我们套用优化枚举[ 1 , n ] [1,\sqrt{n}] [ 1 , n ] O ( n ) O(\sqrt{n}) O ( n )
根据算数基本定理可得,n n n p 1 , p 2 . . . p k p_1,p_2...p_k p 1 , p 2 . . . p k p 1 p_1 p 1 [ 0 , e 1 ] [0,e_1] [ 0 , e 1 ] p 2 p_2 p 2 [ 0 , e 2 ] [0,e_2] [ 0 , e 2 ]
由乘法原理可得,设总因子个数为g ( n ) g(n) g ( n ) e i + 1 e_i+1 e i + 1
g ( n ) = ∏ i = 1 k ( e i + 1 ) g(n)=\prod_{i=1}^{k}(e_i+1) g ( n ) = ∏ i = 1 k ( e i + 1 )
时间复杂度即求素因子分解的复杂度O ( s ) O(s) O ( s )
对于一个正整数p p p n n n n = k p + r n=kp+r n = k p + r k , r k,r k , r 0 ≤ r < p 0\le r<p 0 ≤ r < p k k k n n n p p p r r r n n n p p p n m o d p = r n\,mod\,p =r n m o d p = r
我们定义正整数和整数a , b a,b a , b
a m o d p a\,mod\,p a m o d p
以下公式分别是模p加法,减法,乘法和幂模p
模运算满足结合律,交换律与分配律。
我们用a ≡ b ( m o d m ) a\equiv b\,(mod\,m) a ≡ b ( m o d m ) a a a b b b m m m a a a b b b m m m
对于同余有如下性质
自反性:若a是整数,则a ≡ a ( m o d m ) a\equiv a\,(mod\, m) a ≡ a ( m o d m )
对称性:若a和b是整数,且a ≡ b ( m o d m ) a\equiv b\,(mod\,m) a ≡ b ( m o d m ) b ≡ a ( m o d m ) b\equiv a\,(mod\,m) b ≡ a ( m o d m )
传递性:若a,b,c是整数,且a ≡ b ( m o d m ) a\equiv b\,(mod\,m) a ≡ b ( m o d m ) b ≡ c ( m o d m ) b\equiv c\,(mod\,m) b ≡ c ( m o d m ) a ≡ c ( m o d m ) a\equiv c\,(mod\,m) a ≡ c ( m o d m )
关于同余的加减乘除,若a,b,c,d和m是整数,m > 0 m>0 m > 0 a ≡ b ( m o d m ) a\equiv b\,(mod\,m) a ≡ b ( m o d m ) c ≡ d ( m o d m ) c\equiv d\,(mod\,m) c ≡ d ( m o d m )
加:a + c ≡ b + d ( m o d m ) a+c\equiv b+d\,(mod\,m) a + c ≡ b + d ( m o d m )
减:a − c ≡ b − d ( m o d m ) a-c\equiv b-d\,(mod\,m) a − c ≡ b − d ( m o d m )
乘:a c ≡ b d ( m o d m ) ac\equiv bd\,(mod\,m) a c ≡ b d ( m o d m )
除:在模的左右都同除一个数不能保证同余,后面会讲模除法
寻求最大公约数是人民民主的真谛…
最大的正整数d d d d ∣ a d|a d ∣ a d ∣ b d|b d ∣ b d d d a , b a,b a , b g c d ( a , b ) gcd(a,b) g c d ( a , b ) k ∣ a k|a k ∣ a k ∣ b k|b k ∣ b k ∣ g c d ( a , b ) k|gcd(a,b) k ∣ g c d ( a , b )
由算数基本定理可得,有如下公式满足:
那么g c d ( a , b ) gcd(a,b) g c d ( a , b )
g c d ( a , b ) = p 1 m i n ( x 1 , y 1 ) p 2 m i n ( x 2 , y 2 ) p 3 m i n ( x 3 , y 3 ) . . . p k m i n ( x k , y k ) gcd(a,b)=p_1^{min(x_1,y_1)}p_2^{min(x_2,y_2)}p_3^{min(x_3,y_3)}...p_k^{min(x_k,y_k)} g c d ( a , b ) = p 1 m i n ( x 1 , y 1 ) p 2 m i n ( x 2 , y 2 ) p 3 m i n ( x 3 , y 3 ) . . . p k m i n ( x k , y k )
需要说明的是这里a a a b b b
当b ≠ 0 b\ne0 b = 0 a = k b + r a=kb+r a = k b + r k = ⌊ a b ⌋ , r = a m o d b k=\lfloor\frac{a}{b}\rfloor,r=a\,mod\,b k = ⌊ b a ⌋ , r = a m o d b ( 0 ≤ r < b ) (0\le r<b) ( 0 ≤ r < b ) a − k b a-kb a − k b g c d ( a , b ) = g c d ( b , a m o d b ) gcd(a,b)=gcd(b,a\,mod\,b) g c d ( a , b ) = g c d ( b , a m o d b )
但是假设建立在b ≠ 0 b\ne0 b = 0 b = 0 b=0 b = 0
g c d ( a , b ) = { a b = 0 g c d ( b , a m o d b ) b ≠ 0 gcd(a,b)=\begin{cases} a & b=0 \\ gcd(b,a\,mod\,b) & b\ne 0 \end{cases} g c d ( a , b ) = { a g c d ( b , a m o d b ) b = 0 b = 0
写成代码就是如下
1 2 3 4 5 6 7 int gcd (int a, int b) return !b ? a : gcd (b, a % b); }
也可以用std实现的std::__gcd(a,b)加下划线是不推荐使用因为没有安全保护,但毕竟我们又不是写多线程,直接用就完了。
gcd具有结合律,如下
g c d ( a , b , c , d , e , f , g ) = g c d ( g c d ( a , b ) , c , d , e , f , g ) gcd(a,b,c,d,e,f,g)=gcd(gcd(a,b),c,d,e,f,g) g c d ( a , b , c , d , e , f , g ) = g c d ( g c d ( a , b ) , c , d , e , f , g )
P10463 Interval GCD
给定一个长度为N N N A A A M M M
C l r d,表示把A [ l ] , A [ l + 1 ] , … , A [ r ] A[l],A[l+1],…,A[r] A [ l ] , A [ l + 1 ] , … , A [ r ] d d d
Q l r,表示询问A [ l ] , A [ l + 1 ] , … , A [ r ] A[l],A[l+1],…,A[r] A [ l ] , A [ l + 1 ] , … , A [ r ]
显然线段树,根据gcd的结合律,我们可以进行暴力的单点修改,gcd根据结合律进行维护:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 #include <bits/stdc++.h> #define ll long long #define ls p<<1 #define rs p<<1|1 #define gcd(a,b) __gcd(abs(a),abs(b)) #define pir pair<int,int> using namespace std;const int MN=5e5 +15 ;struct segtree { int l,r; ll sum,d; }t[MN<<2 ]; int n,m;ll a[MN]; void pushup (int p) t[p].sum=t[ls].sum+t[rs].sum; t[p].d=gcd (t[ls].d,t[rs].d); } void build (int p,int l,int r) t[p].l=l; t[p].r=r; if (l==r){ t[p].d=t[p].sum=a[l]-a[l-1 ]; return ; } int mid=l+r>>1 ; build (ls,l,mid); build (rs,mid+1 ,r); pushup (p); } void modify (int p,int x,ll k) if (t[p].l==t[p].r){ t[p].sum+=k; t[p].d+=k; return ; } int mid=t[p].l+t[p].r>>1 ; if (mid>=x) modify (ls,x,k); else modify (rs,x,k); pushup (p); } ll querys (int p,int fl,int fr) { if (t[p].l>=fl&&t[p].r<=fr){ return t[p].sum; } int mid=t[p].l+t[p].r>>1 ; ll ret=0 ; if (mid>=fl){ ret+=querys (ls,fl,fr); } if (mid<fr){ ret+=querys (rs,fl,fr); } return ret; } ll queryd (int p,int fl,int fr) { if (t[p].l>=fl&&t[p].r<=fr){ return t[p].d; } ll ret=0 ; int mid=t[p].l+t[p].r>>1 ; if (mid>=fl){ ret=gcd (ret,queryd (ls,fl,fr)); } if (mid<fr){ ret=gcd (ret,queryd (rs,fl,fr)); } return ret; } int main () ios::sync_with_stdio (0 ); cin>>n>>m; for (int i=1 ;i<=n;i++){ cin>>a[i]; } char op; int l,r; ll v; build (1 ,1 ,n); while (m--) { cin>>op>>l>>r; if (op=='C' ){ cin>>v; modify (1 ,l,v); if (r!=n) modify (1 ,r+1 ,-v); }else { cout<<gcd (queryd (1 ,l+1 ,r),querys (1 ,1 ,l))<<'\n' ; } } return 0 ; }
两个数a和b的最小公倍数是指同时被a和b整除的最小倍数,记为l c m ( a , b ) lcm(a,b) l c m ( a , b )
特殊的,当a和b互素时,l c m ( a , b ) = a b lcm(a,b)=ab l c m ( a , b ) = a b
求LCM需要先求gcd,所以易得
l c m ( a , b ) = a b g c d ( a , b ) lcm(a,b)=\frac{ab}{gcd(a,b)} l c m ( a , b ) = g c d ( a , b ) a b
由算数唯一分解定理可得如下公式:
那么g c d ( a , b ) 和 l c m ( a , b ) gcd(a,b)和lcm(a,b) g c d ( a , b ) 和 l c m ( a , b )
g c d ( a , b ) = p 1 m i n ( x 1 , y 1 ) p 2 m i n ( x 2 , y 2 ) p 3 m i n ( x 3 , y 3 ) . . . p k m i n ( x k , y k ) gcd(a,b)=p_1^{min(x_1,y_1)}p_2^{min(x_2,y_2)}p_3^{min(x_3,y_3)}...p_k^{min(x_k,y_k)} g c d ( a , b ) = p 1 m i n ( x 1 , y 1 ) p 2 m i n ( x 2 , y 2 ) p 3 m i n ( x 3 , y 3 ) . . . p k m i n ( x k , y k )
l c m ( a , b ) = p 1 m a x ( x 1 , y 1 ) p 2 m a x ( x 2 , y 2 ) p 3 m a x ( x 3 , y 3 ) . . . p k m a x ( x k , y k ) lcm(a,b)=p_1^{max(x_1,y_1)}p_2^{max(x_2,y_2)}p_3^{max(x_3,y_3)}...p_k^{max(x_k,y_k)} l c m ( a , b ) = p 1 m a x ( x 1 , y 1 ) p 2 m a x ( x 2 , y 2 ) p 3 m a x ( x 3 , y 3 ) . . . p k m a x ( x k , y k )
需要说明的是这里a a a b b b
我们将gcd和lcm相乘,由下列公式可得
m i n ( x , y ) + m a x ( x , y ) = x + y min(x,y)+max(x,y)=x+y m i n ( x , y ) + m a x ( x , y ) = x + y
可得l c m ( a , b ) × g c d ( a , b ) = a b lcm(a,b)\times gcd(a,b)=ab l c m ( a , b ) × g c d ( a , b ) = a b
等式两边同除g c d ( a , b ) gcd(a,b) g c d ( a , b )
l c m ( a , b ) = a b g c d ( a , b ) lcm(a,b)=\frac{ab}{gcd(a,b)} l c m ( a , b ) = g c d ( a , b ) a b
代码如下
1 2 3 4 5 6 7 int lcm (int a, int b) return a / gcd (a, b) * b; }
裴蜀定理是关于GCD的一个定理。
对于整数a 和 b a和b a 和 b x , y x,y x , y a x + b y = g c d ( a , b ) ax+by=gcd(a,b) a x + b y = g c d ( a , b )
推论:当a和b互素(即g c d ( a , b ) = 1 gcd(a,b)=1 g c d ( a , b ) = 1 a x + b y = 1 ax+by=1 a x + b y = 1
或另一种形式
对于任意x , y x,y x , y d = a x + b y d=ax+by d = a x + b y d d d g c d ( a , b ) gcd(a,b) g c d ( a , b ) g c d ( a , b ) gcd(a,b) g c d ( a , b ) a x + b y = k × g c d ( a , b ) ( k ≥ 1 ) ax+by=k\times gcd(a,b)\,\,(k \ge 1) a x + b y = k × g c d ( a , b ) ( k ≥ 1 ) 证明如下
例题: P4549 【模板】裴蜀定理
给定一个包含n n n 整数 序列A A A A 1 , A 2 , A 3 , . . . , A n A_1,A_2,A_3,...,A_n A 1 , A 2 , A 3 , . . . , A n
求另一个包含n n n 整数 序列X X X S = ∑ i = 1 n A i × X i S=\sum\limits_{i=1}^nA_i\times X_i S = i = 1 ∑ n A i × X i S > 0 S>0 S > 0 S S S
我们可以发现,这个A i × X i A_i\times X_i A i × X i a x + b y ax+by a x + b y a 和 b a和b a 和 b A i × X i A_i\times X_i A i × X i g c d ( A 1 , A 2 ) gcd(A_1,A_2) g c d ( A 1 , A 2 )
引理:g c d ( a 1 , a 2 , . . . a k ) = g c d ( g c d ( a 1 , a 2 ) , g c d ( a 3 , a 4 ) . . . g c d ( a k − 1 , a k ) ) gcd(a_1,a_2,...a_k)=gcd(gcd(a_1,a_2),gcd(a_3,a_4)...gcd(a_{k-1},a_k)) g c d ( a 1 , a 2 , . . . a k ) = g c d ( g c d ( a 1 , a 2 ) , g c d ( a 3 , a 4 ) . . . g c d ( a k − 1 , a k ) )
那么只需要合并结果就可以了
代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <iostream> #include <cmath> #define ll long long using namespace std;ll gcd (ll x,ll y) { if (y==0 ) return x; return gcd (y,x%y); } ll ans,awa; int n;int main () cin>>n; cin>>ans; if (n==1 ){ cout<<ans; return 0 ; } for (int i=2 ;i<=n;i++){ cin>>awa; awa=abs (awa); ans=gcd (ans,awa); } cout<<ans; return 0 ; }
线性同余方程(也叫模线性方程)是最基本的同余方程,即 a x ≡ b ( m o d n ) ax \equiv b(mod \ n) a x ≡ b ( m o d n )
其中 a、b、n 都为常量,x 是未知数,这个方程可以进行一定的转化,得到:a x = k n + b ax = kn + b a x = k n + b
这里的 k 为任意整数,于是我们可以得到更加一般的形式即:a x + b y + c = 0 ax + by + c = 0 a x + b y + c = 0
求解的第一步就是将原式化为a x + b y = c ax+by=c a x + b y = c
第二步求出d = g c d ( a , b ) d=gcd(a,b) d = g c d ( a , b )
d ( a x d + b y d ) = c d(a \frac xd + b \frac yd) = c d ( a d x + b d y ) = c
容易知道( a x d + b y d ) (a \frac xd + b \frac yd) ( a d x + b d y )
第三步:我们由2步可知方程有解则可以一定能表示成a x + b y = c = g c d ( a , b ) × c ax + by = c = gcd(a, b) \times c a x + b y = c = g c d ( a , b ) × c
d = g c d ( a , b ) = g c d ( b , a % b ) ( 1 ) = b x ′ + ( a % b ) y ′ ( 2 ) = b x ′ + [ a − b × ⌊ a b ⌋ ] y ′ ( 3 ) = a y ′ + b [ x ′ − ⌊ a b ⌋ y ′ ] ( 4 ) \begin{aligned} d &= gcd(a, b) \\&= gcd(b, a\%b) & (1)\\&= bx' + (a\%b)y' & (2)\\&= bx' + [a-b \times \lfloor \frac ab \rfloor]y' & (3)\\&= ay' + b[x' - \lfloor \frac ab \rfloor y'] & (4)\end{aligned} d = g c d ( a , b ) = g c d ( b , a % b ) = b x ′ + ( a % b ) y ′ = b x ′ + [ a − b × ⌊ b a ⌋ ] y ′ = a y ′ + b [ x ′ − ⌊ b a ⌋ y ′ ] ( 1 ) ( 2 ) ( 3 ) ( 4 )
于是有{ x = y ′ y = x ′ − ⌊ a b ⌋ y ′ \begin{cases}x &= y' \\ y &= x' - \lfloor \frac ab \rfloor y' \end{cases} { x y = y ′ = x ′ − ⌊ b a ⌋ y ′
需要注意的是,当递归边界即b = 1 b=1 b = 1 x = 1 x=1 x = 1 y = 0 y=0 y = 0
代码也就如下,这样吧x x x y y y
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void exgcd (ll a,ll b,ll &x,ll &y) if (!b){ x=1 ; y=0 ; return ; } exgcd (b,a%b,y,x); y-=a/b*x; }
例如求解方程27 x + 8 y = 1 27x+8y=1 2 7 x + 8 y = 1
点我观看动画!
求关于x x x a x ≡ 1 ( m o d b ) ax \equiv 1 \pmod {b} a x ≡ 1 ( m o d b )
显然可以变化为a x + b y = 1 ax+by=1 a x + b y = 1 g c d ( a , b ) = 1 gcd(a,b)=1 g c d ( a , b ) = 1
对于原式a x + b y = 1 ax+by=1 a x + b y = 1
a x + b y + k × b a − k × b a = 1 ax+by+k\times ba-k\times ba=1 a x + b y + k × b a − k × b a = 1
a ( x + k b ) + b ( y − k a ) = 1 a(x+kb)+b(y-ka)=1 a ( x + k b ) + b ( y − k a ) = 1
即可得求出的解x x x x 0 + k b x_0+kb x 0 + k b
1 2 3 4 5 6 7 8 9 ll a,b,x,y; cin>>a>>b; exgcd (a,b,x,y); cout<<(x%b+b)%b;
可以理解为加上b和减去b不会错过任何解
故AC代码如下,套板子就行
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #define ll long long using namespace std;void exgcd (ll a,ll b,ll &x,ll &y) if (!b){ x=1 ; y=0 ; return ; } exgcd (b,a%b,y,x); y-=a/b*x; } int main () ll a,b,x,y; cin>>a>>b; exgcd (a,b,x,y); cout<<(x%b+b)%b; return 0 ; }
仔细看看这个题,是不是有点眼熟,我们把x x x a − 1 a^{-1} a − 1
要求输出a x + b y = c ax+by=c a x + b y = c x x x y y y
有裴蜀定理可得,如果c c c g c d ( a , b ) gcd(a,b) g c d ( a , b )
用exgcd求出a x 0 + b y 0 = g c d ( a , b ) ax_0+by_0=gcd(a,b) a x 0 + b y 0 = g c d ( a , b ) a x + b y = c ax+by=c a x + b y = c
由裴蜀定理推论得a x + b y = k × g c d ( a , b ) ( k ≥ 1 ) ax+by=k\times gcd(a,b)\,\,(k \ge 1) a x + b y = k × g c d ( a , b ) ( k ≥ 1 )
所以可得a x + b y = c ax+by=c a x + b y = c a x + b y = k × g c d ( a , b ) = c ax+by=k\times gcd(a,b)=c a x + b y = k × g c d ( a , b ) = c
k × g c d ( a , b ) = c k\times gcd(a,b)=c k × g c d ( a , b ) = c
k = c g c d ( a , b ) k=\frac{c}{gcd(a,b)} k = g c d ( a , b ) c
代入原式a x 0 + b y 0 = g c d ( a , b ) ax_0+by_0=gcd(a,b) a x 0 + b y 0 = g c d ( a , b )
x 0 c g c d ( a , b ) a + x 0 c g c d ( a , b ) b = c \frac{x_0c}{gcd(a,b)}a+\frac{x_0c}{gcd(a,b)}b=c g c d ( a , b ) x 0 c a + g c d ( a , b ) x 0 c b = c
故可得x x x y y y
a x + b y = c { x = x 0 × c g c d ( a , b ) y = y 0 × c g c d ( a , b ) ax+by=c\,\begin{cases} x=x_0\times\frac{c}{gcd(a,b)} \\ y=y_0\times\frac{c}{gcd(a,b)} \end{cases} a x + b y = c { x = x 0 × g c d ( a , b ) c y = y 0 × g c d ( a , b ) c
既然我们用x 0 x_0 x 0 y 0 y_0 y 0 x x x y y y
我们开例1推的式子,我们将x 0 x_0 x 0 y 0 y_0 y 0 x 和 y x和y x 和 y
不过我们换元求一下k
m = k b m=kb m = k b
n = k a n=ka n = k a
a ( x 0 + m ) + b ( y 0 − n ) = c a(x_0+m)+b(y_0-n)=c a ( x 0 + m ) + b ( y 0 − n ) = c
展开可得a x 0 + b y 0 + a m − b n = c ax_0+by_0+am-bn=c a x 0 + b y 0 + a m − b n = c
我们只需要让a m − b n = 0 am-bn=0 a m − b n = 0
设g c d ( a , b ) = d gcd(a,b)=d g c d ( a , b ) = d { m = t × b d n = t × a d \begin{cases} m=t\times\frac{b}{d}\\n=t\times\frac{a}{d} \end{cases} { m = t × d b n = t × d a
代入计算得a b d − a b d = 0 \frac{ab}{d}-\frac{ab}{d}=0 d a b − d a b = 0
这时候我们就证明了一个定理
设方程a x + b y = c ax+by=c a x + b y = c x = x 0 , y = y 0 x=x_0,y=y_0 x = x 0 , y = y 0 x = x 0 + b g c d ( a , b ) t , y = y 0 − a g c d ( a , b ) t x=x_0+\frac{b}{gcd(a,b)}t,y=y_0-\frac{a}{gcd(a,b)}t x = x 0 + g c d ( a , b ) b t , y = y 0 − g c d ( a , b ) a t
我们开始考虑最大最小值
{ x = x 0 + t × b d y = y 0 − t × a d \begin{cases} x=x_0+t\times\frac{b}{d}\\y=y_0-t\times\frac{a}{d} \end{cases} { x = x 0 + t × d b y = y 0 − t × d a
我们可以发现当t增大的时候,x越来越大,y越来越小
由于增加减少的值太难写,我们考虑换元法。
令t x = t × b d , t y = t × a d t_x=t\times\frac{b}{d},t_y=t\times\frac{a}{d} t x = t × d b , t y = t × d a
既然是正整数,那么即求x m i n ≥ 1 x_{min}\ge1 x m i n ≥ 1
代入上式可得
x 0 + k t x ≥ 1 x_0+kt_x\ge1 x 0 + k t x ≥ 1
变形即可得
k ≥ ⌈ 1 − x 0 t x ⌉ k\ge\lceil\frac{1-x_0}{t_x}\rceil k ≥ ⌈ t x 1 − x 0 ⌉
为什么是上取整因为k必须大于这个值
可得x m i n = x 0 − ⌈ 1 − x 0 t x ⌉ x_{min}=x_0-\lceil\frac{1-x_0}{t_x}\rceil x m i n = x 0 − ⌈ t x 1 − x 0 ⌉
x m i n x_min x m i n y m a x y_{max} y m a x y m a x < 0 y_{max}<0 y m a x < 0
懒的敲式子了
代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 #include <iostream> #include <cmath> #define ll long long using namespace std;int T;ll exgcd (ll a,ll b,ll &x,ll &y) { if (!b){ x=1 ; y=0 ; return a; } ll d=exgcd (b,a%b,y,x); y-=a/b*x; return d; } int main () cin>>T;ll qp (ll a,ll b,ll mod) { a%=mod; ll res=1 ; while (b>0 ){ if (b&1 ){ res=res*a%mod; } a=a*a%mod; b>>=1 ; } return res; } while (T--) { ll a,b,c,x,y; cin>>a>>b>>c; ll d=exgcd (a,b,x,y); if (c%d!=0 ){ cout<<-1 <<endl; continue ; } x=x*c/d,y=y*c/d; ll tx=b/d,ty=a/d; ll k=ceil ((1.0 -x)/tx); x+=tx*k; y-=ty*k; if (y<=0 ){ ll ansy=y+ty*(ll)1 *ceil ((1.0 -y)/ty); cout<<x<<" " <<ansy<<endl; }else { cout<<(y-1 )/ty+1 <<" " <<x<<" " <<(y-1 )%ty+1 <<" " <<x+(y-1 )/ty*tx<<" " <<y<<endl; } } return 0 ; }
总结以下就是这个结论
已知三个正整数a , b , c ( a , b , c < = 1 0 5 ) a,b,c(a,b,c<=10^5) a , b , c ( a , b , c < = 1 0 5 ) a b m o d c a^{b}\mod c a b m o d c
直接模拟一个b次的循环,枚举a对b次乘法
1 2 3 4 5 6 7 8 9 10 11 12 13 int f (int a, int b, int c) int ans = 1 ; while (b--) ans = ans * a; return ans % c; }
显然我们发现1 0 1 0 5 10^{10^5} 1 0 1 0 5
并且时间复杂度是O ( b ) O(b) O ( b )
a b m o d c = ( a m o d c ) ( b m o d c ) m o d c ab\mod c=(a\mod c)(b\mod c)\mod c a b m o d c = ( a m o d c ) ( b m o d c ) m o d c
证明贴一个别人的
改进如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int f (int a, int b, int c) a = (a % c + c) % c; int ans = 1 % c; while (b--) ans = ans * a % c; return ans; }
但是时间复杂度并没有改善。
我们采用二分的思想,对原式进行分治法,有如下公式。
a b m o d c = { 1 m o d c b 为 0 a ( a ( b − 1 2 ) 2 m o d c b 为奇数 ( a b / 2 ) 2 m o d c b 为偶数 a^{b}\mod c=\begin{cases} 1\mod c & b为0\\a(a^{(b-1}{2})^{2}\mod c & b为奇数 \\ (a^{b/2})^2\mod c & b为偶数 \end{cases} a b m o d c = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 m o d c a ( a ( b − 1 2 ) 2 m o d c ( a b / 2 ) 2 m o d c b 为 0 b 为 奇 数 b 为 偶 数
于是我们可以利用程序的递归思想,把函数描述成如下形式
f ( a , b , c ) = { 1 m o d c b 为 0 a f ( a , b − 1 2 , c ) 2 b 为奇数 f ( a , b 2 , c ) 2 b 为偶数 f(a,b,c)=\begin{cases} 1\mod c & b为0\\ af(a,\frac{b-1}{2},c)^2 & b为奇数 \\ f(a,\frac{b}{2},c)^2 & b为偶数\end{cases} f ( a , b , c ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 m o d c a f ( a , 2 b − 1 , c ) 2 f ( a , 2 b , c ) 2 b 为 0 b 为 奇 数 b 为 偶 数
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ll qp (ll a,ll b,ll mod) { a%=mod; ll res=1 ; while (b>0 ){ if (b&1 ){ res=res*a%mod; } a=a*a%mod; b>>=1 ; } return res; }
注意如果乘法可能溢出,要使用龟速乘!
对于正整数n n n φ ( n ) \varphi(n) φ ( n ) φ ( 1 ) = 1 \varphi(1)=1 φ ( 1 ) = 1
即φ ( n ) = ∑ i = 1 n [ g c d ( i , n ) = 1 ] \varphi(n)=\sum\limits_{i=1}^n[gcd(i,n)=1] φ ( n ) = i = 1 ∑ n [ g c d ( i , n ) = 1 ]
其中[ A ] [A] [ A ] A 成立时, [ A ] = 1 ,反之 [ A ] = 0 A成立时,[A]=1,反之[A]=0 A 成 立 时 , [ A ] = 1 , 反 之 [ A ] = 0
对于素数p p p p p p
φ ( p ) = p − 1 \varphi(p)=p-1 φ ( p ) = p − 1
对于素数的幂来说,有
φ ( p k ) = p k − p k − 1 \varphi(p^k)=p^k-p^{k-1} φ ( p k ) = p k − p k − 1
对于素数p p p
φ ( 2 p ) = φ ( p ) \varphi(2p)=\varphi(p) φ ( 2 p ) = φ ( p )
对于任意正整数n,有
n = ∑ d ∣ n φ ( d ) n=\sum\limits_{d|n}\varphi(d) n = d ∣ n ∑ φ ( d )
对于任意两个互素的数p , q p,q p , q
φ ( p q ) = φ ( p ) × φ ( q ) \varphi(pq)=\varphi(p)\times\varphi(q) φ ( p q ) = φ ( p ) × φ ( q )
利用算数基本定理可得
故有任意正整数n,有
φ ( n ) = n ∏ i = 1 k ( 1 − 1 p i ) \varphi(n)=n\prod^k_{i=1}(1-\frac{1}{p_i}) φ ( n ) = n ∏ i = 1 k ( 1 − p i 1 )
我们可以用定义来做,那么只需要枚举i i i g c d ( n , i ) = 1 gcd(n,i)=1 g c d ( n , i ) = 1
φ ( n ) = n ∏ i = 1 k ( p i − 1 p i ) \varphi(n)=n\prod^k_{i=1}(\frac{p_i-1}{p_i}) φ ( n ) = n ∏ i = 1 k ( p i p i − 1 )
- 对[ 2 , n ] [2,\sqrt{n}] [ 2 , n ] p p p p ∣ n p|n p ∣ n a n s = a n s / ( i − 1 i ) ans=ans/(\frac{i-1}{i}) a n s = a n s / ( i i − 1 ) n / = i n/=i n / = i
当某个时刻n=1的时候直接返回ans的值。若试除完后还有剩余说明n是一个素数,返回a n s / ( n − 1 n ) ans/(\frac{n-1}{n}) a n s / ( n n − 1 ) 代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 int phi (int n) int ans=n; for (int i=2 ;i*i<=n;i++){ if (n%i==0 ){ ans=ans/i*(i-1 ); while (n%i==0 ) { n/=i; } } } if (n>=2 ){ ans=ans/n*(n-1 ); } return ans; }
先除后乘防止超Int范围
因为欧拉函数是积性函数,φ ( x y ) = φ ( x ) φ ( y ) \varphi(xy)=\varphi(x)\varphi(y) φ ( x y ) = φ ( x ) φ ( y )
可得如下筛法,时间复杂度O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 phi[1 ]=1 ; for (int i=2 ;i<=n;i++) { if (!vis[i]) p[++cnt]=i,phi[i]=i-1 ; for (int j=1 ;p[j]&&i*p[j]<=n;j++) { vis[i*p[j]]=1 ; if (!(i%p[j])) { phi[i*p[j]]=phi[i]*p[j]; break ; } else phi[i*p[j]]=phi[i]*(p[j]-1 ); } }
数论函数指定义域为正整数的函数。
若数论函数f f f gcd ( a , b ) = 1 \gcd(a,b)=1 g cd( a , b ) = 1 f ( 1 ) = 1 f(1)=1 f ( 1 ) = 1 f ( a b ) = f ( a ) f ( b ) f(ab)=f(a)f(b) f ( a b ) = f ( a ) f ( b ) f f f
若数论函数f f f a , b a,b a , b f ( a b ) = f ( a ) f ( b ) f(ab)=f(a)f(b) f ( a b ) = f ( a ) f ( b ) f f f
单位函数ϵ ( n ) = [ n = 1 ] \epsilon(n)=[n=1] ϵ ( n ) = [ n = 1 ]
常函数1 ( n ) = 1 1(n)=1 1 ( n ) = 1
幂函数I k ( n ) = n k I_k(n)=n^k I k ( n ) = n k
恒等函数i d ( n ) = n \mathrm{id}(n)=n i d ( n ) = n i d k ( n ) = n k \mathrm{id}_k(n)=n^k i d k ( n ) = n k
因数和函数σ ( n ) = ∑ d ∣ n d \sigma(n)=\sum_{d|n}d σ ( n ) = ∑ d ∣ n d σ k ( n ) = ∑ d ∣ n d k \sigma_k(n)=\sum_{d|n}d^k σ k ( n ) = ∑ d ∣ n d k
约数个数d ( n ) = σ 0 ( n ) = ∑ d ∣ n 1 d(n)=\sigma_0(n)=\sum_{d|n}1 d ( n ) = σ 0 ( n ) = ∑ d ∣ n 1
经典永流传~
例题:CF920F
给定n n n a a a m m m 1 ≤ n , m ≥ 3 × 1 0 5 , 1 ≤ a i ≤ 1 0 6 1 \le n,m \ge 3\times 10^5,1\le a_{i}\le 10^6 1 ≤ n , m ≥ 3 × 1 0 5 , 1 ≤ a i ≤ 1 0 6
将i ∈ [ l , r ] i \in [l,r] i ∈ [ l , r ] a i a_i a i d ( a i ) d(a_i) d ( a i ) 求∑ i = l r a i \sum\limits_{i=l}^{r}a_i i = l ∑ r a i 这里阐述一个估算d ( x ) d(x) d ( x )
那么这个题很好做,不难根据表发现当a i = 1 0 6 , d ( a i ) = 240 a_i=10^6,d(a_i)=240 a i = 1 0 6 , d ( a i ) = 2 4 0
故有代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 #include <bits/stdc++.h> #define ls p<<1 #define rs p<<1|1 #define ll long long using namespace std;const int MN=3e5 +15 ,MA=1e6 +15 ;template <typename type>inline void read (type &x) x=0 ;bool flag (0 ) char ch=getchar (); while (!isdigit (ch)) flag=ch=='-' ,ch=getchar (); while (isdigit (ch)) x=(x<<1 )+(x<<3 )+(ch^48 ),ch=getchar (); flag?x=-x:0 ; } struct segtree { int l,r; bool isok; ll sum; }t[MN<<2 ]; ll a[MN]; int n,m; int d[MA],num[MA];vector<bool > vis (MA) ;vector<int > prime; void pushup (int p) t[p].sum=t[ls].sum+t[rs].sum; if (t[ls].isok==1 &&t[rs].isok==1 ){ t[p].isok=1 ; } } void build (int p,int l,int r) t[p].l=l; t[p].r=r; if (l==r){ t[p].sum=a[l]; if (t[p].sum==1 ||t[p].sum==2 ){ t[p].isok=1 ; } return ; } int mid=l+r>>1 ; build (ls,l,mid); build (rs,mid+1 ,r); pushup (p); } void update (int p,int fl,int fr) if (t[p].isok) return ; if (t[p].l==t[p].r){ t[p].sum=d[t[p].sum]; if (t[p].sum==1 ||t[p].sum==2 ) t[p].isok=1 ; return ; } int mid=t[p].l+t[p].r>>1 ; if (mid>=fl) update (ls,fl,fr); if (mid<fr) update (rs,fl,fr); pushup (p); } ll query (int p,int fl,int fr) { if (t[p].l>=fl&&t[p].r<=fr){ return t[p].sum; } ll ret=0 ; int mid=t[p].l+t[p].r>>1 ; if (mid>=fl)ret+=query (ls,fl,fr); if (mid<fr) ret+=query (rs,fl,fr); return ret; } void getd () d[1 ]=1 ; for (int i=2 ;i<MA;i++){ if (!vis[i]){ prime.push_back (i); d[i]=2 ; num[i]=1 ; } for (int j=0 ;1ll *i*prime[j]<MA&&j<prime.size ();j++){ vis[i*prime[j]]=1 ; if (i%prime[j]==0 ){ num[i*prime[j]]=num[i]+1 ; d[i*prime[j]]=d[i]/(num[i]+1 )*(num[i*prime[j]]+1 ); break ; }else { d[i*prime[j]]=d[i]*2 ; num[i*prime[j]]=1 ; } } } } int main () ios::sync_with_stdio (0 ); getd (); read (n); read (m); for (int i=1 ;i<=n;i++){ read (a[i]); } int op,x,y; build (1 ,1 ,n); while (m--) { read (op); read (x); read (y); if (op==1 ){ update (1 ,x,y); }else { cout<<query (1 ,x,y)<<'\n' ; } } }
n n n a a a n , a n,a n , a a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)} \equiv 1(\mod n) a φ ( n ) ≡ 1 ( m o d n )
证明?
推论:
若正整数a , b a,b a , b a x ≡ 1 ( m o d b ) a^x \equiv 1 \pmod b a x ≡ 1 ( m o d b ) x 0 x_0 x 0 φ ( b ) \varphi(b) φ ( b )
可以用欧拉定理反证法证明。
例题:洛谷P1463_POI_2001_HAOI_2007_反素数
若p p p g c d ( a , p ) = 1 gcd(a,p)=1 g c d ( a , p ) = 1 a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1(\mod p) a p − 1 ≡ 1 ( m o d p ) a a a a p ≡ a ( m o d p ) a^p\equiv a(\mod p) a p ≡ a ( m o d p )
我们回到判定素数的那一节,如果我们要判定的范围超过的1 0 12 10^{12} 1 0 1 2 O ( n ) O(\sqrt{n}) O ( n )
我们可以用费马小定理,随机找几个和n n n a a a
计算a n − 1 m o d n a^{n-1} \mod n a n − 1 m o d n
若结果均为1,那么认为n n n O ( C l o g 2 n ) O(Clog_2n) O ( C l o g 2 n )
但是,以上假设不成立!
因为在费马小定理的条件中,若置换条件。
若a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1(\mod p) a p − 1 ≡ 1 ( m o d p ) p p p
例如561,这一类数我们称其为伪素数,又称为卡迈克尔数,在n ≤ 1 0 9 n\le 10^9 n ≤ 1 0 9
若n n n 2 n − 1 2^n-1 2 n − 1
Miller Rabin素性检验是一种素数判定的法则,由CMU的教授Miller首次提出,并由希大的Rabin教授作出修改,变成了今天竞赛人广泛使用的一种算法,故称Miller Rabin素性检验。
本质其实是随机化算法,能在时间复杂度为O ( C log 3 n ) O(C \log^3 n) O ( C log 3 n ) C C C
既然我们单纯费马小定理无法判断,我们只好引入新的定理来提高我们的正确性。
二次探测定理:对于质数p p p x 2 ≡ 1 ( m o d p ) x^2 \equiv 1 \pmod p x 2 ≡ 1 ( m o d p ) p p p x 1 = 1 , x 2 = p − 1 x_1=1,x_2=p-1 x 1 = 1 , x 2 = p − 1
证明:
x 2 ≡ 1 ( m o d p ) x 2 − 1 ≡ 0 ( m o d p ) ( x + 1 ) ( x − 1 ) ≡ 0 ( m o d p ) p ∣ ( x + 1 ) ( x − 1 ) ∵ p 是质数 ∴ { x 1 = 1 x 2 = p − 1 \begin{aligned} x^2 & \equiv 1 \pmod p \\ x^{2}-1 & \equiv 0 \pmod p \\ (x+1)(x-1) & \equiv 0 \pmod p \\ p &| (x+1)(x-1) \\ \\ \because &p \text{是质数} \\ \\ \therefore &\begin{cases} x_1=1 \\ x_{2}= p-1\\ \end{cases} \end{aligned} x 2 x 2 − 1 ( x + 1 ) ( x − 1 ) p ∵ ∴ ≡ 1 ( m o d p ) ≡ 0 ( m o d p ) ≡ 0 ( m o d p ) ∣ ( x + 1 ) ( x − 1 ) p 是质数 { x 1 = 1 x 2 = p − 1
这个定理有什么用?
如果费马小定理检测得到a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod p a p − 1 ≡ 1 ( m o d p ) p − 1 p-1 p − 1 p p p a p − 1 a^{p-1} a p − 1 x 2 x^2 x 2
拆分为( a p − 1 2 ) 2 ≡ 1 ( m o d p ) \left(a^{\dfrac{p-1}{2}}\right)^2 \equiv 1 \pmod p ⎝ ⎛ a 2 p − 1 ⎠ ⎞ 2 ≡ 1 ( m o d p )
如果a p − 1 2 a^{\frac{p-1}{2}} a 2 p − 1 ( m o d p ) \pmod p ( m o d p ) p − 1 p-1 p − 1 p p p
如果( a p − 1 2 ) 2 ≡ 1 ( m o d p ) \left(a^{\frac{p-1}{2}}\right)^2 \equiv 1 \pmod p ( a 2 p − 1 ) 2 ≡ 1 ( m o d p ) a p − 1 4 a^{\frac{p-1}{4}} a 4 p − 1
也就是说,我们可以将p − 1 = u × 2 t p-1=u\times 2^t p − 1 = u × 2 t u u u a u , a u × 2 , a u × 2 2 … a^u,a^{u\times 2},a^{u \times 2^2} \dots a u , a u × 2 , a u × 2 2 … p − 1 p-1 p − 1 p − 1 p-1 p − 1 p p p
过程如下:
先特判 3 以下的数和偶数 将n − 1 n-1 n − 1 u × 2 t u\times 2^t u × 2 t 选取多个底数a a a a u , a u × 2 , a u × 2 2 … a^u,a^{u\times 2},a^{u \times 2^2} \dots a u , a u × 2 , a u × 2 2 … p − 1 p-1 p − 1 如果都满足,则认为为素数。 板子题:SP288——PON
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 #include <bits/stdc++.h> #define ll long long using namespace std;constexpr ll prime[]={2 ,3 ,5 ,7 ,11 ,13 ,17 ,37 };ll qmul (ll a,ll b,ll MOD) { ll ret=0 ; while (b){ if (b&1 ) ret=(ret+a)%MOD; b>>=1 ; a=(a+a)%MOD; } return ret; } ll qpow (ll a,ll b,ll MOD) { ll ret=1 ; while (b){ if (b&1 ) ret=qmul (ret,a,MOD); a=qmul (a,a,MOD); b>>=1 ; } return ret; } bool MillerRabin (ll n) if (n<3 ||n%2 ==0 ) return n==2 ; ll d=n-1 ,tot=0 ; while (d%2 ==0 ) d/=2 ,++tot; for (auto p:prime){ ll v=qpow (p,d,n); if (v==1 ||v==n-1 ||v==0 ) continue ; for (int j=1 ;j<=tot;j++){ v=qmul (v,v,n); if (v==n-1 &&j!=tot){ v=1 ; break ; } if (v==1 ) return 0 ; } if (v!=1 ) return 0 ; } return 1 ; } int main () int T; cin>>T; while (T--){ ll n; cin>>n; cout<<(MillerRabin (n)?"YES\n" :"NO\n" ); } return 0 ; }
给出一个大整数n ( 1 ≤ n ≤ 1 0 100000 ) n(1\le n \le 10^{100000}) n ( 1 ≤ n ≤ 1 0 1 0 0 0 0 0 )
求2 n m o d 1 e 9 + 7 2^n\mod 1e9+7 2 n m o d 1 e 9 + 7
令x = p − 1 x=p-1 x = p − 1
2 p − 1 m o d p = 1 2^{p-1}\mod p=1 2 p − 1 m o d p = 1
m = n m o d ( p − 1 ) m=n\mod(p-1) m = n m o d ( p − 1 ) m ∈ [ 0 , p − 1 ) m \in [0,p-1) m ∈ [ 0 , p − 1 )
说到这里,我们先来看看欧拉定理的局限性
欧拉定理:
n n n a a a n , a n,a n , a a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)} \equiv 1(\mod n) a φ ( n ) ≡ 1 ( m o d n )
不难发现,局限性在于互素,即g c d ( a , n ) = 1 gcd(a,n)=1 g c d ( a , n ) = 1
拓展欧拉定理如下:
定义:
a b ≡ { a ( b m o d φ ( m ) ) g c d ( a , m ) = 1 a b g c d ( a , m ) ≠ 1 , b < φ ( m ) a ( ( b + φ ( m o d φ ( m ) ) g c d ( a , m ) ≠ 1 , ( b ≥ φ ( m ) ( m o d m ) a^b \equiv \begin{cases} a^{(b \mod \varphi(m))} & gcd(a,m)=1 \\ a^b & gcd(a,m) \ne 1,b< \varphi(m) \\ a^{((b+\varphi(\,mod \,\varphi(m))} & gcd(a,m)\ne 1,(b\ge \varphi(m) \end{cases} \quad (mod\,\,\,\,m) a b ≡ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a ( b m o d φ ( m ) ) a b a ( ( b + φ ( m o d φ ( m ) ) g c d ( a , m ) = 1 g c d ( a , m ) = 1 , b < φ ( m ) g c d ( a , m ) = 1 , ( b ≥ φ ( m ) ( m o d m )
其中第二行的意思,若g c d ( a , m ) ≠ 1 , b < φ ( m ) gcd(a,m) \ne 1,b< \varphi(m) g c d ( a , m ) = 1 , b < φ ( m )
题目中的m m m b < φ ( m ) b<\varphi(m) b < φ ( m )
证明略(啊?)
应用:
P5091 【模板】扩展欧拉定理
求a b m o d m a^b \mod m a b m o d m
其中1 ≤ a ≤ 1 0 9 , 1 ≤ b ≤ 1 0 20000000 , 1 ≤ m ≤ 1 0 8 1\le a\le 10^9,1\le b\le10^{20000000},1\le m \le 10^8 1 ≤ a ≤ 1 0 9 , 1 ≤ b ≤ 1 0 2 0 0 0 0 0 0 0 , 1 ≤ m ≤ 1 0 8
十分甚至九分的恐怖,甚至都没有互素,直接套上去看看。
φ ( x ) \varphi(x) φ ( x ) b b b
代码?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 #include <iostream> #define ll long long using namespace std;int phi (int n) int ans=n; for (int i=2 ;i*i<=n;i++){ if (n%i==0 ){ ans=ans/i*(i-1 ); while (n%i==0 ) { n/=i; } } } if (n>=2 ){ ans=ans/n*(n-1 ); } return ans; } inline int read (int mod) int x=0 ; bool g=false ; char c=getchar (); while (c<'0' ||c>'9' ) c=getchar (); while (c>='0' &&c<='9' ) { x=(x<<3 )+(x<<1 )+(c^'0' ); if (x>=mod) x%=mod,g=true ; c=getchar (); } if (g) return (x+mod); else return x; } ll quickpow (ll a,ll b,ll mod) { ll ret=1 ; while (b) { if (b&1 ){ ret=ret*a%mod; } a=a*a%mod; b>>=1 ; } return ret%mod; } int main () ll a,mod,cishu; cin>>a>>mod; cishu=read (phi (mod)); cout<<quickpow (a,cishu,mod); return 0 ; }
定义:
形如
a x ≡ b ( m o d m ) ax \equiv b \,\,\, (mod \,m) a x ≡ b ( m o d m )
的方程称为线性同余方程,其中a , b , m a,b,m a , b , m x x x [ 0 , m − 1 ] [0,m-1] [ 0 , m − 1 ] x x x x x x
逆元可以理解为模意义下的除法,符号为a − 1 a^{-1} a − 1
可以理解为倒数eee,然而实际上不是倒数,人家就叫做逆元。
考虑最简单的情况,g c d ( a , m ) = 1 gcd(a,m)=1 g c d ( a , m ) = 1 a a a a a a
线性方程组解的数量等于g c d ( a , n ) gcd(a,n) g c d ( a , n )
我们可以将取余的式子改写为如下的形式:
a x + n y = b ax+ny=b a x + n y = b
不难发现可以用拓展欧几里得算法求解该方程,得一组解,在通过之前上面讲过的单一解求通解,在拓展到全体解,即可得到。
其实说实话这两个不是一种东西吗…
其实是等价的。
例题:
P1082 [NOIP2012 提高组] 同余方程
求关于x x x a x ≡ 1 ( m o d b ) ax \equiv 1 \pmod {b} a x ≡ 1 ( m o d b )
不是这个题怎么又上来了?
然而实际上这个题刚好就能作为例题eee
代码重放
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #define ll long long using namespace std;void exgcd (ll a,ll b,ll &x,ll &y) if (!b){ x=1 ; y=0 ; return ; } exgcd (b,a%b,y,x); y-=a/b*x; } int main () ll a,b,x,y; cin>>a>>b; exgcd (a,b,x,y); cout<<(x%b+b)%b; return 0 ; }
乘法逆元就是求a b m o d p = a × x m o d p \frac{a}{b} \mod p=a\times x \mod p b a m o d p = a × x m o d p x x x
那么也就是说a b ≡ a × x (mod p) \frac{a}{b} \equiv a\times x \,\text{(mod p)} b a ≡ a × x (mod p)
那么有1 ≡ b × x (mod p) 1\equiv b\times x \,\text{(mod p)} 1 ≡ b × x (mod p)
由费马小定理可得当p p p x = b ( p − 2 ) x=b^{(p-2)} x = b ( p − 2 )
快速幂即可求解。
留存一份,一般是先exgcd或快速幂求解f [ n ] f[n] f [ n ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 jc[0 ] = 1 ; for (int i = 1 ; i <= 1e5 ; i++) { jc[i] = (i * jc[i - 1 ]) % MOD; } ll x, y; inv[100000 ] = binpow (jc[100000 ], MOD - 2 ); for (int i = 100000 - 1 ; i >= 0 ; i--) { inv[i] = inv[i + 1 ] * (i + 1 ) % MOD; }
「物不知数」问题:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
答:我不会,我不会,我不会,啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊┗( T﹏T )┛
中国剩余定理可以求解如下的一元线性同余方程组。
{ x ≡ a 1 m o d n 1 x ≡ a 2 m o d n 2 ⋮ x ≡ a n m o d n k \begin{cases} x\equiv a_{1} \mod n_{1}\\ x\equiv a_{2} \mod n_{2} \\ \space \space \space\ \ \vdots \\ x\equiv a_{n} \mod n_{k}\end{cases} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x ≡ a 1 m o d n 1 x ≡ a 2 m o d n 2 ⋮ x ≡ a n m o d n k
其中n 1 , n 2 … n k n_1,n_{2} \ldots n_{k} n 1 , n 2 … n k
方法:
计算所有模数的积:n n n
对于第i i i
- 计算m i = n n i m_i=\frac{n}{n_i} m i = n i n
- 计算m i m_i m i n i n_i n i m i − 1 m_i^{-1} m i − 1
- 计算c i = m i ∗ m i − 1 c_i=m_{i}* m_i^{-1} c i = m i ∗ m i − 1
方程组在模n n n P1495 【模板】中国剩余定理(CRT)/ 曹冲养猪
实现代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 #include <iostream> #define ll long long using namespace std;const int MN=1e5 +15 ;int a[MN],b[MN],n;ll mt=1 ; ll exgcd (ll a,ll b,ll &x,ll &y) { if (!b){ x=1 ; y=0 ; return a; } ll d=exgcd (b,a%b,y,x); y-=a/b*x; return d; } ll inv (ll a,ll n) { ll x,y; exgcd (a,n,x,y); return (x%n+n)%n; } long long quick_mul (long long x,long long y,long long mod) long long ans=0 ; while (y!=0 ){ if (y&1 ==1 )ans+=x,ans%=mod; x=x+x,x%=mod; y>>=1 ; } return ans; } ll crt () { ll ans=0 ; for (int i=1 ;i<=n;i++){ ll m=mt/a[i],invm=inv (m,a[i]); ll ci=m*invm; ans=(ans+quick_mul (b[i],ci,mt))%mt; } return (ans%mt+mt)%mt; } int main () cin>>n; for (int i=1 ;i<=n;i++){ cin>>a[i]>>b[i]; mt*=a[i]; } cout<<crt (); return 0 ; }
{ x ≡ a 1 m o d n 1 x ≡ a 2 m o d n 2 ⋮ x ≡ a n m o d n k \begin{cases} x\equiv a_{1} \mod n_{1}\\ x\equiv a_{2} \mod n_{2} \\ \space \space \space\ \ \vdots \\ x\equiv a_{n} \mod n_{k}\end{cases} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x ≡ a 1 m o d n 1 x ≡ a 2 m o d n 2 ⋮ x ≡ a n m o d n k
其中n 1 , n 2 … n k n_1,n_{2} \ldots n_{k} n 1 , n 2 … n k
与中国剩余定理的区别在哪里?在于我们需要合并方程才能做,例如合并上面两个式子:
x ≡ a 1 m o d n 1 x\equiv a_{1} \mod n_{1} x ≡ a 1 m o d n 1
x ≡ a 2 m o d n 2 x \equiv a_{2}\mod n_2 x ≡ a 2 m o d n 2
合并为:x ≡ a ′ m o d ( n 1 n 2 / g c d ( m 1 , m 2 ) ) x\equiv a' \mod (n_1n_{2}/ gcd(m_1,m_2)) x ≡ a ′ m o d ( n 1 n 2 / g c d ( m 1 , m 2 ) )
若合并了所有方程,那么得到的解即为最终解。
证明:
根据方程可变形为:
x ≡ a 1 + n 1 y 1 x\equiv a_1+n_1y_1 x ≡ a 1 + n 1 y 1
x ≡ a 2 + n 2 y 2 x\equiv a_2+n_2y_2 x ≡ a 2 + n 2 y 2
可得:a 1 + n 1 y 1 = a 2 + n 2 y 2 ⇒ n 1 y 1 − m 2 y 2 = a 2 − a 1 a_1+n_1y_1=a_2+n_2y_{2}\Rightarrow n_1y_1-m_2y_2=a_2-a_1 a 1 + n 1 y 1 = a 2 + n 2 y 2 ⇒ n 1 y 1 − m 2 y 2 = a 2 − a 1
转换为经典的a x + b y = c ax+by=c a x + b y = c a x + b y = g c d ( a , b ) ax+by=gcd(a,b) a x + b y = g c d ( a , b )
通过上面变形过的方程够再出一个m o d m 1 m 2 / g c d ( m 1 , m 2 ) \mod m_1m_2/gcd(m_1,m_2) m o d m 1 m 2 / g c d ( m 1 , m 2 )
即得证。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 #include <iostream> #define ll long long using namespace std;const int MN=1e5 +15 ;ll md[MN],b[MN],mt; int n; ll slowti (ll a,ll b,ll mod) { ll ret=0 ; while (b>0 ) { if (b&1 ) ret=(ret+a)%mod; a=(a+a)%mod; b>>=1 ; } return ret; } ll exgcd (ll a,ll b,ll &x,ll &y) { if (!b){ x=1 ; y=0 ; return a; } ll ret=exgcd (b,a%b,y,x); y-=a/b*x; return ret; } ll excrt () { ll x,y; ll m1=md[1 ],b1=b[1 ]; ll ans=(b1%m1+m1)%m1; for (int i=2 ;i<=n;i++){ ll m2=md[i],b2=b[i]; ll a=m1,b=m2,c=(b2-b1%m2+m2)%m2; ll d=exgcd (a,b,x,y); if (c%d!=0 ){ return -1 ; } x=slowti (x,c/d,b/d); ans=b1+x*m1; m1=m2/d*m1; ans=(ans%m1+m1)%m1; b1=ans; } return ans; } int main () cin>>n; for (int i=1 ;i<=n;i++){ cin>>md[i]>>b[i]; } cout<<excrt (); return 0 ; }
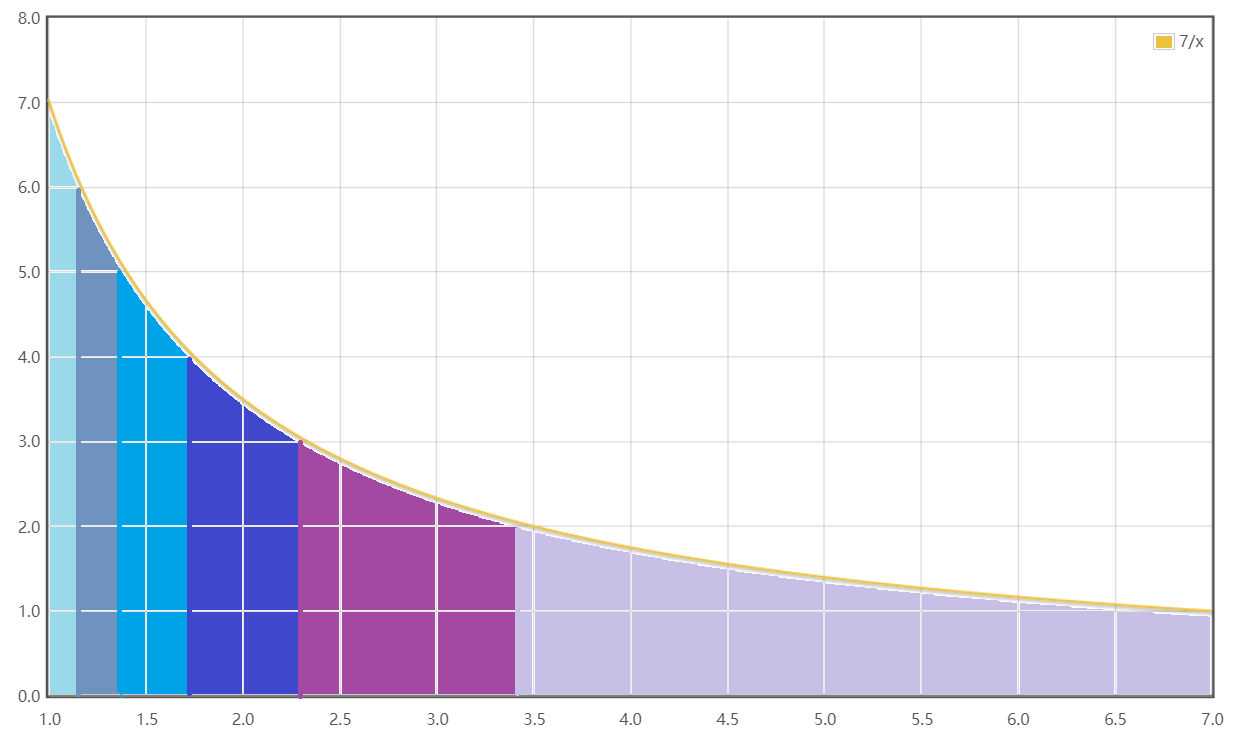
求∑ i = 1 n ⌊ n i ⌋ \sum\limits_{i=1}^n \lfloor \frac{n}{i} \rfloor i = 1 ∑ n ⌊ i n ⌋ n ≤ 1 0 12 n\le 10^{12} n ≤ 1 0 1 2
第一眼看上去是不可做题,因为如果我们直接暴力枚举的话是肯定不行的,因为我们枚举到1 0 9 10^9 1 0 9
我们比如果举例一个函数,比如果y = 15 x y=\frac{15}{x} y = x 1 5
我们根据题意,把他的下取整表示出来(图中红色):
有没有发现什么,发现对应的下取整都是一个横线端(这不废话吗 ),而且是分成一小段一小段的。
或者我们搬一个图来举例(出处vvauted的数论分块 :
没错,数论分块中的分块就是看中的这一点,图像中是被分割成了几个大块,只要我们不断枚举块,就能显著的降低时间复杂度!
但是问题在于我们怎么知道每个块的右端点?这里给出一个引理。
对于任意一个i i i ⌊ n i ⌋ = ⌊ n j ⌋ \lfloor \frac{n}{i} \rfloor=\lfloor \frac{n}{j} \rfloor ⌊ i n ⌋ = ⌊ j n ⌋ j j j
j = ⌊ n ⌊ n i ⌋ ⌋ j=\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor j = ⌊ ⌊ i n ⌋ n ⌋
证明如下:
⌊ n i ⌋ ≤ n i \lfloor \frac{n}{i} \rfloor \le \frac{n}{i} ⌊ i n ⌋ ≤ i n
⌊ n ⌊ n i ⌋ ⌋ ≥ ⌊ n n i ⌋ \lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor \ge \lfloor \frac{n}{\frac{n}{i}}\rfloor ⌊ ⌊ i n ⌋ n ⌋ ≥ ⌊ i n n ⌋
⌊ n ⌊ n i ⌋ ⌋ ≥ i \lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor \ge i ⌊ ⌊ i n ⌋ n ⌋ ≥ i
得证。
复杂度分析:
当x ∈ [ 1 , ⌊ n ⌋ ] x\in[1,\lfloor \sqrt{n} \rfloor] x ∈ [ 1 , ⌊ n ⌋ ] ⌊ n ⌋ \lfloor \sqrt{n} \rfloor ⌊ n ⌋
当x ∈ [ ⌊ n ⌋ , n ] x\in[\lfloor \sqrt{n} \rfloor,n] x ∈ [ ⌊ n ⌋ , n ] ⌊ n ⌋ \lfloor \sqrt{n} \rfloor ⌊ n ⌋
共2 ⌊ n ⌋ 2\lfloor \sqrt{n} \rfloor 2 ⌊ n ⌋ O ( n ) O(\sqrt{n}) O ( n )
求∑ i = 1 n f ( i ) \sum\limits_{i=1}^{n}f(i) i = 1 ∑ n f ( i ) n ≤ 1 0 6 n\le 10^6 n ≤ 1 0 6
f ( i ) f(i) f ( i ) i i i
对于i i i [ 1 , n ] [1,n] [ 1 , n ] ⌊ n i ⌋ \lfloor \frac{n}{i} \rfloor ⌊ i n ⌋
∑ i = 1 n f ( i ) = ∑ i = 1 n ⌊ n i ⌋ \sum\limits_{i=1}^n f(i)=\sum\limits_{i=1}^n \lfloor \frac{n}{i} \rfloor i = 1 ∑ n f ( i ) = i = 1 ∑ n ⌊ i n ⌋
那么其实可以直接O ( n ) O(n) O ( n )
但是如果n ≤ 1 0 14 n\le 10^{14} n ≤ 1 0 1 4
我们考虑一个块怎么贡献,根据式子,其实就是( r − l + 1 ) × ⌊ n i ⌋ (r-l+1)\times \lfloor \frac{n}{i} \rfloor ( r − l + 1 ) × ⌊ i n ⌋
那么代码也就如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> #define ll long long using namespace std;int main () ll n,ans=0 ; cin>>n; for (ll i=1 ,j;i<=n;i=j+1 ){ j=n/(n/i); ans+=(j-i+1 )*(n/i); } cout<<ans; return 0 ; }
给定n , k n,k n , k ∑ i = 1 n k m o d n \sum\limits_{i=1}^n k \mod n i = 1 ∑ n k m o d n n , k ≤ 1 0 9 n,k\le 10^9 n , k ≤ 1 0 9
这个题很有数论分块的感觉,毕竟这已经不能O ( n ) O(n) O ( n )
简单转换一下,把取模变成如下式子:
∑ i = 1 n k − ⌊ k i ⌋ × i \sum\limits_{i=1}^{n} k-\lfloor \frac{k}{i} \rfloor \times i i = 1 ∑ n k − ⌊ i k ⌋ × i
= n × k − ∑ i = 1 n ⌊ k i ⌋ × i =n\times k - \sum\limits_{i=1}^n \lfloor \frac{k}{i} \rfloor \times i = n × k − i = 1 ∑ n ⌊ i k ⌋ × i
直接数论分块就可以了,但是这个我们再算贡献的时候与∑ i = l r i \sum\limits_{i=l}^r i i = l ∑ r i
那么代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <bits/stdc++.h> #define ll long long using namespace std;ll n,k,ret=0 ; ll getsum (ll l,ll r) { if (r>n) r=n; return (r-l+1 )*(l+r)/2 ; } int main () cin>>n>>k; ret+=n*k; for (ll i=1 ,j;i<=n;i=j+1 ){ if (k/i==0 ) break ; j=k/(k/i); if (j>n) j=n; ret-=(k/i)*getsum (i,j); } cout<<ret; return 0 ; }
定义f ( n ) = ∑ i ∣ n i f(n)=\sum\limits_{i|n} i f ( n ) = i ∣ n ∑ i x , y x,y x , y [ x , y ] [x,y] [ x , y ] f f f
x , y ≤ 1 0 9 x,y \le 10^9 x , y ≤ 1 0 9
简单的拆成两个前缀和的形式,现在只需要求出[ 1 , n ] [1,n] [ 1 , n ]
∑ i = 1 n f ( i ) = ∑ i = 1 n ∑ k ∣ i k \sum\limits_{i=1}^n f(i)=\sum\limits_{i=1}^n\sum\limits_{k|i} k i = 1 ∑ n f ( i ) = i = 1 ∑ n k ∣ i ∑ k
交换一下求和顺序:
∑ k = 1 n ∑ k ∣ i k ( k ≤ n ) \sum\limits_{k=1}^n\sum\limits_{k|i}k(k\le n) k = 1 ∑ n k ∣ i ∑ k ( k ≤ n )
不难发现转化为了约数为k的数的前缀和,那么直接做就可以了。即为∑ k = 1 n k × ⌊ n k ⌋ \sum\limits_{k=1}^{n} k\times \lfloor \frac{n}{k} \rfloor k = 1 ∑ n k × ⌊ k n ⌋
那么直接写就没了。。。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> #define ll long long using namespace std;ll n,m; ll getsum (ll l,ll r) { return (r-l+1 )*(l+r)/2 ; } int main () cin>>n>>m; n--; ll retn=0 ,retm=0 ; for (ll i=1 ,j;i<=n;i=j+1 ){ j=n/(n/i); retn+=(n/i)*getsum (i,j); } for (ll i=1 ,j;i<=m;i=j+1 ){ j=m/(m/i); retm+=(m/i)*getsum (i,j); } cout<<retm-retn; return 0 ; }
这个只是属于一个工具,如果考这个复杂度是显然可以观察出来的,往下取整的式子推就可以了。
证明一般可能省略或给出。
狄利克雷卷积,是定义在数论函数 间的一种二元运算,有如下两个等价定义:
( f ∗ g ) ( n ) = ∑ x y = n f ( x ) g ( y ) (f*g)(n)=\sum\limits_{xy=n}f(x)g(y) ( f ∗ g ) ( n ) = x y = n ∑ f ( x ) g ( y )
或如下等价式:
( f ∗ g ) ( n ) = ∑ d ∣ n f ( d ) g ( n d ) (f*g)(n)=\sum\limits_{d|n}f(d)g(\frac{n}{d}) ( f ∗ g ) ( n ) = d ∣ n ∑ f ( d ) g ( d n )
积性函数之间的狄利克雷卷积有一个重要的性质:
若f , g f,g f , g f ∗ g f*g f ∗ g
证明如下:
显然有( f ∗ g ) ( 1 ) = f ( 1 ) g ( 1 ) = 1 (f*g)(1)=f(1)g(1)=1 ( f ∗ g ) ( 1 ) = f ( 1 ) g ( 1 ) = 1 a , b a,b a , b
( f ∗ g ) ( a ) = ∑ d ∣ a f ( d ) g ( a d ) , ( f ∗ g ) ( b ) = ∑ d ∣ b f ( d ) g ( b d ) (f*g)(a)=\sum\limits_{d|a}f(d)g(\frac{a}{d}),(f*g)(b)=\sum\limits_{d|b}f(d)g(\frac{b}{d}) ( f ∗ g ) ( a ) = d ∣ a ∑ f ( d ) g ( d a ) , ( f ∗ g ) ( b ) = d ∣ b ∑ f ( d ) g ( d b )
( f ∗ g ) ( a b ) = ∑ d ∣ a b f ( d ) g ( a b d ) (f*g)(ab)=\sum\limits_{d|ab}f(d)g(\frac{ab}{d}) ( f ∗ g ) ( a b ) = d ∣ a b ∑ f ( d ) g ( d a b )
注意到:
\begin{align} \sum\limits_{d|a}f(d)g(\frac{a}{d}) \cdot \sum\limits_{d|b}f(d)g(\frac{b}{d}) & = \sum\limits_{d_1|a,d_2|b}f(d_1)g(\frac{a}{d_1}) \cdot f(d_2)g(\frac{b}{d_2})\\ \sum\limits_{d|a}f(d)g(\frac{a}{d}) \cdot \sum\limits_{d|b}f(d)g(\frac{b}{d}) & = \sum\limits_{d_1|a,d_2|b}f(d_1d_2)g(\frac{ab}{d_1d_2}) \end{align}
因为a , b a,b a , b a b ab a b a , b a,b a , b
那么若f , g f,g f , g f ∗ g f*g f ∗ g
( f ∗ g ) ( a ) ⋅ ( f ∗ g ) ( b ) = ( f ∗ g ) ( a b ) (f*g)(a) \cdot (f*g)(b) =(f*g)(ab) ( f ∗ g ) ( a ) ⋅ ( f ∗ g ) ( b ) = ( f ∗ g ) ( a b )
根据定义有( f ∗ 1 ) ( n ) = ∑ d ∣ n f ( d ) 1 ( n d ) = ∑ d ∣ n f ( d ) (f*1)(n)=\sum\limits_{d|n}f(d)1(\frac{n}{d})=\sum\limits_{d|n}f(d) ( f ∗ 1 ) ( n ) = d ∣ n ∑ f ( d ) 1 ( d n ) = d ∣ n ∑ f ( d )
所以得:
( I d k ∗ 1 ) ( n ) = ∑ d ∣ n I d k ( d ) = ∑ d ∣ n d k = σ k (Id_k * 1)(n) =\sum\limits_{d|n} Id_k(d) =\sum\limits_{d|n} d^k = \sigma _k ( I d k ∗ 1 ) ( n ) = d ∣ n ∑ I d k ( d ) = d ∣ n ∑ d k = σ k
因为:
( φ ∗ 1 ) ( n ) = ∑ d ∣ n φ ( d ) (\varphi * 1)(n)=\sum\limits_{d|n} \varphi(d) ( φ ∗ 1 ) ( n ) = d ∣ n ∑ φ ( d )
当d = p m d=p^m d = p m p p p
∑ d ∣ n φ ( d ) = φ ( 1 ) + ∑ i = 1 m φ ( p i ) = p m = d \sum\limits_{d|n} \varphi(d) =\varphi(1)+\sum\limits_{i=1}^m \varphi(p^i) = p^m = d d ∣ n ∑ φ ( d ) = φ ( 1 ) + i = 1 ∑ m φ ( p i ) = p m = d
那么可得( φ ∗ 1 ) ( p m ) = p m (\varphi * 1)(p^m)=p^m ( φ ∗ 1 ) ( p m ) = p m
那么现在设n n n ( φ ∗ 1 ) ( p m ) (\varphi * 1)(p^m) ( φ ∗ 1 ) ( p m )
( φ ∗ 1 ) ( Π p m ) = Π ( φ ∗ 1 ) ( p m ) = Π p m (\varphi * 1)(\Pi p^m)=\Pi (\varphi * 1)(p^m)=\Pi p^m ( φ ∗ 1 ) ( Π p m ) = Π ( φ ∗ 1 ) ( p m ) = Π p m
即得:
( φ ∗ 1 ) ( n ) = n (\varphi * 1)(n)=n ( φ ∗ 1 ) ( n ) = n
φ ∗ 1 = I d \varphi * 1 =Id φ ∗ 1 = I d
e e e μ \mu μ 有如下关系式:
e = μ ∗ 1 = ∑ d ∣ n μ ( d ) e=\mu*1=\sum\limits_{d|n}\mu(d) e = μ ∗ 1 = d ∣ n ∑ μ ( d )
证明利用单位元(下面)性质即可,略。
接下来我们来阐述狄利克雷卷积的一些性质:
具有交换性:( f ∗ g ) ( n ) = ( g ∗ f ) ( n ) (f*g)(n)=(g*f)(n) ( f ∗ g ) ( n ) = ( g ∗ f ) ( n ) 具有结合律:( ( f ∗ g ) ∗ h ) ( n ) = ( f ∗ ( g ∗ h ) ) ( n ) ((f*g)*h)(n)=(f*(g*h))(n) ( ( f ∗ g ) ∗ h ) ( n ) = ( f ∗ ( g ∗ h ) ) ( n ) 对函数加法的分配率:( f ∗ ( g + h ) ) ( n ) = ( f ∗ g ) ( n ) + ( f ∗ h ) ( n ) (f*(g+h))(n)=(f*g)(n)+(f*h)(n) ( f ∗ ( g + h ) ) ( n ) = ( f ∗ g ) ( n ) + ( f ∗ h ) ( n ) 单位元:
( ε ∗ f ) ( n ) = ∑ d ∣ n ε ( d ) f ( n d ) = f ( n ) (\varepsilon * f)(n)=\sum\limits_{d|n}\varepsilon(d)f(\frac{n}{d})=f(n) ( ε ∗ f ) ( n ) = d ∣ n ∑ ε ( d ) f ( d n ) = f ( n )
故单位函数即为狄利克雷卷积的单位元。
逆元:
假设f ∗ g = ε f*g=\varepsilon f ∗ g = ε g g g f f f f − 1 f^{-1} f − 1
f f f 必要条件 是f ( 1 ) ≠ 0 f(1)\neq 0 f ( 1 ) = 0
f − 1 f^{-1} f − 1
对于证明过程可以去网上找,这里就不在叙述了。
对于莫比乌斯函数的定义我们这里不在详细叙述,需要去积性函数那里找。
莫比乌斯函数是积性函数,于是我们可以用线性筛来筛!
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 vector<bool > vis (MN) ;vector<ll> prime; ll n,mu[MN]; void euler () vis[1 ]=1 ; mu[1 ]=1 ; for (int i=2 ;i<=n;i++){ if (!vis[i]){ prime.push_back (i); mu[i]=-1 ; } for (auto p:prime){ if (i*p>n) break ; vis[p*i]=1 ; if (i%p==0 ){ mu[i*p]=0 ; break ; } mu[i*p]=-mu[i]; } } }
莫比乌斯函数还具有另一个性质:
∑ d ∣ n μ ( d ) = [ n = 1 ] \sum\limits_{d|n}\mu(d)=[n=1] d ∣ n ∑ μ ( d ) = [ n = 1 ]
证明需用到组合计数,这里就不在叙述了。
那么我们就能根据推论得到一个反演常用的结论 :
∑ d ∣ g c d ( i , j ) μ ( d ) = [ g c d ( i , j ) = 1 ] \sum\limits_{d|gcd(i,j)}\mu(d)=[gcd(i,j)=1] d ∣ g c d ( i , j ) ∑ μ ( d ) = [ g c d ( i , j ) = 1 ]
但是到现在我们还并没有说反演到底是啥,我们下面就来说。
设f ( n ) , g ( n ) f(n),g(n) f ( n ) , g ( n )
如果有:
f ( n ) = ( g ∗ 1 ) ( n ) = ∑ d ∣ n g ( d ) f(n)=(g*1)(n)=\sum\limits_{d|n}g(d) f ( n ) = ( g ∗ 1 ) ( n ) = d ∣ n ∑ g ( d )
那么有:
g ( n ) = ( μ ∗ f ) ( n ) = ∑ d ∣ n μ ( d ) f ( n d ) g(n)=(\mu * f)(n)=\sum\limits_{d|n}\mu(d) f(\frac{n}{d}) g ( n ) = ( μ ∗ f ) ( n ) = d ∣ n ∑ μ ( d ) f ( d n )
证明运用卷积即可。
有如下式子:
∑ i = 1 n ∑ j = 1 m f ( g c d ( i , j ) ) \sum\limits_{i=1}^{n}\sum\limits_{j=1}^mf(gcd(i,j)) i = 1 ∑ n j = 1 ∑ m f ( g c d ( i , j ) )
一般套路:
我们可以尝试构造出函数g g g
f = ( g ∗ 1 ) = ∑ d ∣ n g ( d ) f=(g*1)=\sum\limits_{d|n}g(d) f = ( g ∗ 1 ) = d ∣ n ∑ g ( d )
不难替换:
∑ i = 1 n ∑ j = 1 m ∑ d ∣ g c d ( i , j ) g ( d ) \sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|gcd(i,j)}g(d) i = 1 ∑ n j = 1 ∑ m d ∣ g c d ( i , j ) ∑ g ( d )
不难发现当d ∣ g c d ( i , j ) d|gcd(i,j) d ∣ g c d ( i , j ) d ∣ i d|i d ∣ i d ∣ j d|j d ∣ j d ∣ i d|i d ∣ i d ∣ j d|j d ∣ j
∑ d = 1 g ( d ) ∑ i = 1 n [ d ∣ i ] ∑ j = 1 m [ d ∣ j ] \sum\limits_{d=1}g(d)\sum\limits_{i=1}^n [d|i]\sum\limits_{j=1}^m [d|j] d = 1 ∑ g ( d ) i = 1 ∑ n [ d ∣ i ] j = 1 ∑ m [ d ∣ j ]
不难发现后面两项就是在枚举约数个数,可以转化为⌊ n d ⌋ ⌊ m d ⌋ \lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor ⌊ d n ⌋ ⌊ d m ⌋
最终式为:
∑ d = 1 g ( d ) ⌊ n d ⌋ ⌊ m d ⌋ \sum\limits_{d=1}g(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor d = 1 ∑ g ( d ) ⌊ d n ⌋ ⌊ d m ⌋
即得,数论分块求解即可。
例1.1 :
∑ i = 1 n ∑ j = 1 m g c d ( i , j ) \sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j) i = 1 ∑ n j = 1 ∑ m g c d ( i , j )
不难发现其实就是I d ( g c d ( i , j ) ) Id(gcd(i,j)) I d ( g c d ( i , j ) )
∑ d = 1 φ ( d ) ⌊ n d ⌋ ⌊ m d ⌋ \sum\limits_{d=1}\varphi(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor d = 1 ∑ φ ( d ) ⌊ d n ⌋ ⌊ d m ⌋
例1.2:
∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = 1 ] \sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=1] i = 1 ∑ n j = 1 ∑ m [ g c d ( i , j ) = 1 ]
不难发现是单位函数e e e
∑ d = 1 μ ( d ) ⌊ n d ⌋ ⌊ m d ⌋ \sum\limits_{d=1}\mu(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor d = 1 ∑ μ ( d ) ⌊ d n ⌋ ⌊ d m ⌋
例2:
∑ x = a b ∑ y = c d [ g c d ( x , y ) = k ] \sum\limits_{x=a}^b\sum\limits_{y=c}^d [gcd(x,y)=k] x = a ∑ b y = c ∑ d [ g c d ( x , y ) = k ]
其中1 ≤ a , b , c , d , k ≤ 5 × 1 0 4 1\le a,b,c,d,k\le 5\times 10^4 1 ≤ a , b , c , d , k ≤ 5 × 1 0 4
这种区间,我们可以套路的转化为前缀和的形式,用容斥原理求解,那么不难转化:
f ( n , m ) = ∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = k ] f(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=k] f ( n , m ) = i = 1 ∑ n j = 1 ∑ m [ g c d ( i , j ) = k ]
考虑把k k k
∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ m k ⌋ [ g c d ( i , j ) = 1 ] \sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}[gcd(i,j)=1] i = 1 ∑ ⌊ k n ⌋ j = 1 ∑ ⌊ k m ⌋ [ g c d ( i , j ) = 1 ]
套入例1.2
∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ m k ⌋ ∑ d ∣ g c d ( i , j ) μ ( d ) \sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}\sum\limits_{d|gcd(i,j)}\mu(d) i = 1 ∑ ⌊ k n ⌋ j = 1 ∑ ⌊ k m ⌋ d ∣ g c d ( i , j ) ∑ μ ( d )
考虑下取整的式子能否直接代入,其实是可以的。那么有
∑ d = 1 μ ( d ) ⌊ n k d ⌋ ⌊ m k d ⌋ \sum\limits_{d=1}\mu(d)\lfloor\frac{n}{kd}\rfloor\lfloor\frac{m}{kd}\rfloor d = 1 ∑ μ ( d ) ⌊ k d n ⌋ ⌊ k d m ⌋
线性筛求μ \mu μ O ( n ) O(n) O ( n )
例3:
∑ i = 1 n ∑ j = 1 n ( i j ∗ g c d ( i , j ) ) m o d m \sum\limits_{i=1}^n\sum\limits_{j=1}^n(ij*gcd(i,j)) \mod m i = 1 ∑ n j = 1 ∑ n ( i j ∗ g c d ( i , j ) ) m o d m
上来发现式子有点不像人样,尝试枚举gcd,有:
∑ d = 1 d ∑ i = 1 n ∑ j = 1 n i j [ g c d ( i , j ) = d ] \sum\limits_{d=1}d\sum\limits_{i=1}^n\sum\limits_{j=1}^nij[gcd(i,j)=d] d = 1 ∑ d i = 1 ∑ n j = 1 ∑ n i j [ g c d ( i , j ) = d ]
我们发现这个式子和例2及其详细,我们可以转化过去,但是注意i j → i d ∗ j d ij\rightarrow id*jd i j → i d ∗ j d
∑ d = 1 d ∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ n k ⌋ [ g c d ( i , j ) = 1 ] ∗ i d ∗ j d \sum\limits_{d=1}d\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}[gcd(i,j)=1]*id*jd d = 1 ∑ d i = 1 ∑ ⌊ k n ⌋ j = 1 ∑ ⌊ k n ⌋ [ g c d ( i , j ) = 1 ] ∗ i d ∗ j d
考虑把d d d
∑ d = 1 d 3 ∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ n k ⌋ [ g c d ( i , j ) = 1 ] ∗ i j \sum\limits_{d=1}d^3\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}[gcd(i,j)=1]*ij d = 1 ∑ d 3 i = 1 ∑ ⌊ k n ⌋ j = 1 ∑ ⌊ k n ⌋ [ g c d ( i , j ) = 1 ] ∗ i j
现在把例二丢进去:
∑ d = 1 d 3 ∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ n k ⌋ i j ∑ k ∣ g c d ( i , j ) μ ( k ) \sum\limits_{d=1}d^3\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{k}\rfloor}ij\sum\limits_{k|gcd(i,j)}\mu(k) d = 1 ∑ d 3 i = 1 ∑ ⌊ k n ⌋ j = 1 ∑ ⌊ k n ⌋ i j k ∣ g c d ( i , j ) ∑ μ ( k )
如果我们想转化成最终形式,我们考虑i j ij i j i j ij i j
∑ d = 1 d 3 ∑ k = 1 μ ( k ) k 2 ∑ i = 1 ⌊ n k d ⌋ ∑ j = 1 ⌊ n k d ⌋ i j \sum\limits_{d=1}d^3\sum\limits_{k=1}\mu(k)k^2\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{n}{kd}\rfloor}ij d = 1 ∑ d 3 k = 1 ∑ μ ( k ) k 2 i = 1 ∑ ⌊ k d n ⌋ j = 1 ∑ ⌊ k d n ⌋ i j
有没有发现多了个k 2 k^2 k 2 i j ij i j k k k k 2 k^2 k 2
考虑后面式子,后面式子我们其实可以O ( 1 ) O(1) O ( 1 )
f ( ⌊ n k d ⌋ , ⌊ m k d ⌋ ) = ∑ i = 1 ⌊ n k d ⌋ i ∑ j = 1 ⌊ n k d ⌋ j = ⌊ n k d ⌋ × ( ⌊ n k d ⌋ + 1 ) 2 × ⌊ m k d ⌋ × ( ⌊ m k d ⌋ + 1 ) 2 f(\lfloor\frac{n}{kd}\rfloor,\lfloor\frac{m}{kd}\rfloor)=\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{n}{kd}\rfloor}j=\frac{\lfloor\frac{n}{kd}\rfloor\times(\lfloor\frac{n}{kd}\rfloor+1)}{2}\times\frac{\lfloor\frac{m}{kd}\rfloor\times(\lfloor\frac{m}{kd}\rfloor+1)}{2} f ( ⌊ k d n ⌋ , ⌊ k d m ⌋ ) = i = 1 ∑ ⌊ k d n ⌋ i j = 1 ∑ ⌊ k d n ⌋ j = 2 ⌊ k d n ⌋ × ( ⌊ k d n ⌋ + 1 ) × 2 ⌊ k d m ⌋ × ( ⌊ k d m ⌋ + 1 )
考虑前面的式子,发现枚举没有上界或者上界很大,我们能不能限制上界?
发现分式中的k d kd k d n n n t = k d t=kd t = k d
考虑枚举d d d k k k
∑ t = 1 n ∑ d ∣ t d 3 μ ( t d ) ( t d ) 2 f ( ⌊ n t ⌋ , ⌊ n t ⌋ ) \sum\limits_{t=1}^n\sum\limits_{d|t}d^3\mu(\frac{t}{d})(\frac{t}{d})^2f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor) t = 1 ∑ n d ∣ t ∑ d 3 μ ( d t ) ( d t ) 2 f ( ⌊ t n ⌋ , ⌊ t n ⌋ )
考虑把立方和平方消去:
∑ t = 1 n t 2 f ( ⌊ n t ⌋ , ⌊ n t ⌋ ) ∑ d ∣ t d μ ( t d ) \sum\limits_{t=1}^nt^2f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor)\sum\limits_{d|t}d\mu(\frac{t}{d}) t = 1 ∑ n t 2 f ( ⌊ t n ⌋ , ⌊ t n ⌋ ) d ∣ t ∑ d μ ( d t )
后面的式子其实就是∑ d ∣ n I d ( d ) μ ( T ) = φ ( t ) \sum\limits_{d|n}Id(d)\mu(T)=\varphi(t) d ∣ n ∑ I d ( d ) μ ( T ) = φ ( t )
不难有:
∑ t = 1 n t 2 φ ( t ) f ( ⌊ n t ⌋ , ⌊ n t ⌋ ) \sum\limits_{t=1}^{n}t^2\varphi(t)f(\lfloor\frac{n}{t}\rfloor,\lfloor\frac{n}{t}\rfloor) t = 1 ∑ n t 2 φ ( t ) f ( ⌊ t n ⌋ , ⌊ t n ⌋ )
到这里我们完成80%,不难发现后面O ( 1 ) O(1) O ( 1 )
原式为∑ i = 1 n I d 2 ( i ) φ ( i ) \sum\limits_{i=1}^nId_2(i)\varphi(i) i = 1 ∑ n I d 2 ( i ) φ ( i )
我们需要构造函数g g g
∑ d ∣ n I d 2 ( d ) φ ( d ) g ( n d ) \sum\limits_{d|n}Id_2(d)\varphi(d)g(\frac{n}{d}) d ∣ n ∑ I d 2 ( d ) φ ( d ) g ( d n )
能够快速求出。
考虑直接把I d 2 Id_2 I d 2
令g = I d 2 g=Id_2 g = I d 2
那么原式I d 2 Id_2 I d 2
∑ d ∣ n d 2 φ ( d ) ( n d ) 2 = n 2 ∑ d ∣ n φ ( d ) = n 3 \sum\limits_{d|n}d^2\varphi(d)(\frac{n}{d})^2=n^2\sum\limits_{d|n}\varphi(d)=n^3 d ∣ n ∑ d 2 φ ( d ) ( d n ) 2 = n 2 d ∣ n ∑ φ ( d ) = n 3
最后一个式子考虑反演变为I d Id I d
那么这道题做完了,不难发现g g g O ( n ) O(n) O ( n )
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 #include <bits/stdc++.h> #define ll long long using namespace std;constexpr int MN = 2e6 + 15 ;ll inv2, inv6, P, n, fsum[MN + 15 ], phi[MN + 15 ]; unordered_map<ll, ll> ump; vector<bool > vis (MN + 15 ) ;vector<ll> prm; inline ll read () ll x = 0 , t = 1 ; char ch = getchar (); while ((ch < '0' || ch > '9' ) && ch != '-' ) ch = getchar (); if (ch == '-' ) t = -1 , ch = getchar (); while (ch <= '9' && ch >= '0' ) x = x * 10 + ch - 48 , ch = getchar (); return x * t; } ll ksm (ll a, ll b) ll ret = 1 ; while (b) { if (b & 1 ) { ret = (ret * a) % P; } a = a * a % P; b >>= 1 ; } return ret; } ll getlf (ll k) k %= P; return ((k * (k + 1 ) % P * inv2 % P) * (k * (k + 1 ) % P * inv2 % P)) % P; } ll getpf (ll k) k %= P; return (k * (k + 1 ) % P * (2 * k + 1 ) % P * inv6 % P) % P; } void getphi () vis[0 ] = vis[1 ] = 1 ; phi[1 ] = 1 ; for (ll i = 2 ; i <= MN; i++) { if (!vis[i]) { prm.push_back (i); phi[i] = i - 1 ; } for (auto p : prm) { if (p * i > MN) break ; vis[p * i] = 1 ; if (i % p == 0 ) { phi[i * p] = phi[i] * p; break ; } else phi[i * p] = phi[i] * (p - 1 ); } } for (ll i = 1 ; i <= MN; i++) { fsum[i] = (fsum[i - 1 ] + i * i * phi[i] % P) % P; } } ll dushu (ll k) if (k <= MN) return fsum[k]; if (ump[k]) return ump[k]; ll ans = getlf (k), now, pre; for (ll i = 2 , j; i <= k; i = j + 1 ) { j = k / (k / i); ans = (ans - (getpf (j) - getpf (i - 1 )) % P * dushu (k / i) % P) % P; } return ump[k] = (ans + P) % P; } ll solve () ll ans = 0 , pre = 0 , now; for (ll i = 1 , j; i <= n; i = j + 1 ) { j = n / (n / i); now = dushu (j); ans = (ans + ((now - pre) * getlf (n / i)) % P) % P; pre = now; } return (ans + P) % P; } int main () P = read (); n = read (); getphi (); inv6 = ksm (6 , P - 2 ); inv2 = ksm (2 , P - 2 ); cout << solve (); return 0 ; }
真服了好多次模拟赛考这个自己都不会转化导致就只能在那里坐牢。
二项式反演用于解决 “某个物品恰好 若干个” 这一类计数例题。
我们记f n f_n f n n n n g n g_n g n n n n i ( i ≥ 0 ) i(i\ge 0) i ( i ≥ 0 )
若已知g n g_n g n f i f_i f i
f n = ∑ i = 0 n ( n i ) ( − 1 ) n − i g i f_n=\sum\limits_{i=0}^n \binom{n}{i} (-1)^{n-i} g_i f n = i = 0 ∑ n ( i n ) ( − 1 ) n − i g i
证明过程如下:
f n = ∑ i = 0 n ( n i ) ( − 1 ) n − i g i f n = ∑ i = 0 n ( n i ) ( − 1 ) n − i [ ∑ j = 0 i ( i j ) f j ] f n = ∑ i = 0 n ∑ j = 0 i ( n i ) ( i j ) ( − 1 ) n − i f j \begin{aligned} f_n&=\sum\limits_{i=0}^n \binom{n}{i}(-1)^{n-i}g_{i}\\ f_n&=\sum\limits_{i=0}^n \binom{n}{i}(-1)^{n-i} \left[ \sum\limits_{j=0}^i \binom{i}{j}f_{j} \right]\\ f_n&=\sum\limits_{i=0}^n\sum\limits_{j=0}^i \binom{n}{i} \binom{i}{j} (-1)^{n-i} f_j \end{aligned} f n f n f n = i = 0 ∑ n ( i n ) ( − 1 ) n − i g i = i = 0 ∑ n ( i n ) ( − 1 ) n − i [ j = 0 ∑ i ( j i ) f j ] = i = 0 ∑ n j = 0 ∑ i ( i n ) ( j i ) ( − 1 ) n − i f j
考虑交换求和顺序,为了满足j ≤ i j\le i j ≤ i j j j i i i
f n = ∑ i = 0 n ∑ j = 0 i ( n i ) ( i j ) ( − 1 ) n − i f j = ∑ j = 0 n f j ∑ i = j n ( n i ) ( i j ) ( − 1 ) n − i ∵ ( n i ) ( i j ) = ( n j ) ( n − j i − j ) ∴ ∑ j = 0 n f j ∑ i = j n ( n j ) ( n − j i − j ) ( − 1 ) n − i = ∑ j = 0 n ( n j ) f j ∑ i = j n ( n − j i − j ) ( − 1 ) n − i \begin{aligned} f_n&=\sum\limits_{i=0}^n\sum\limits_{j=0}^i \binom{n}{i} \binom{i}{j} (-1)^{n-i} f_j \\ & = \sum\limits_{j=0}^nf_{j}\sum\limits_{i=j}^n \binom{n}{i} \binom{i}{j} (-1)^{n-i} \\ \\ & \because \binom{n}{i}\binom{i}{j}=\binom{n}{j}\binom{n-j}{i-j} \\ & \therefore \sum\limits_{j=0}^nf_{j}\sum\limits_{i=j}^n \binom{n}{j} \binom{n-j}{i-j} (-1)^{n-i} \\ \\ & =\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{i=j}^n \binom{n-j}{i-j} (-1)^{n-i} \\ \end{aligned} f n = i = 0 ∑ n j = 0 ∑ i ( i n ) ( j i ) ( − 1 ) n − i f j = j = 0 ∑ n f j i = j ∑ n ( i n ) ( j i ) ( − 1 ) n − i ∵ ( i n ) ( j i ) = ( j n ) ( i − j n − j ) ∴ j = 0 ∑ n f j i = j ∑ n ( j n ) ( i − j n − j ) ( − 1 ) n − i = j = 0 ∑ n ( j n ) f j i = j ∑ n ( i − j n − j ) ( − 1 ) n − i
设k = i − j k=i-j k = i − j ∵ i ∈ [ j , n ] \because i\in [j,n] ∵ i ∈ [ j , n ] ∴ k ∈ [ 0 , n − j ] \therefore k\in [0,n-j] ∴ k ∈ [ 0 , n − j ]
f n = ∑ j = 0 n ( n j ) f j ∑ i = j n ( n − j i − j ) ( − 1 ) n − i = ∑ j = 0 n ( n j ) f j ∑ k = 0 n − j ( n − j k ) ( − 1 ) n − j − k ∵ ∑ i = 0 n ( − 1 ) n − i ( n i ) = [ n = 0 ] ∴ f n = ∑ i = 0 n ( n j ) f j [ n − j = 0 ] = ∑ i = 0 n ( n j ) f j [ n = j ] = f n ∵ f n = f n ∴ 得证 \begin{aligned} f_n&=\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{i=j}^n \binom{n-j}{i-j} (-1)^{n-i} \\ &=\sum\limits_{j=0}^n \binom{n}{j} f_{j}\sum\limits_{k=0}^{n-j} \binom{n-j}{k} (-1)^{n-j-k} \\ & \because \sum\limits_{i=0}^n (-1)^{n-i}\binom{n}{i}=[n=0] \\ \\ \therefore f_n&=\sum\limits_{i=0}^n \binom{n}{j}f_{j}[n-j=0] \\ & = \sum\limits_{i=0}^n \binom{n}{j}f_{j}[n=j] \\ & =f_{n}\\ \\ & \because f_n=f_{n}\\ & \therefore \text{得证} \end{aligned} f n ∴ f n = j = 0 ∑ n ( j n ) f j i = j ∑ n ( i − j n − j ) ( − 1 ) n − i = j = 0 ∑ n ( j n ) f j k = 0 ∑ n − j ( k n − j ) ( − 1 ) n − j − k ∵ i = 0 ∑ n ( − 1 ) n − i ( i n ) = [ n = 0 ] = i = 0 ∑ n ( j n ) f j [ n − j = 0 ] = i = 0 ∑ n ( j n ) f j [ n = j ] = f n ∵ f n = f n ∴ 得证
而做题过程中往往遇见的是g n g_n g n f n f_n f n
那么二项式反演就是干这个的,利用g n g_n g n f n f_n f n
形式1:
g n g_n g n n n n f n f_n f n n n n
g n = ∑ i = 0 n ( n i ) f i ⇔ f n = ∑ i = 0 n ( − 1 ) n − i ( n i ) g i g_n=\sum\limits_{i=0}^n \binom{n}{i} f_{i}\Leftrightarrow f_{n}= \sum\limits_{i=0}^n (-1)^{n-i} \binom{n}{i} g_i g n = i = 0 ∑ n ( i n ) f i ⇔ f n = i = 0 ∑ n ( − 1 ) n − i ( i n ) g i
形式2:
g k g_k g k k k k f k f_k f k k k k
g k = ∑ i = k n ( i k ) f i ⇔ f k = ∑ i = 0 n ( − 1 ) i − k ( i k ) g i g_k=\sum\limits_{i=k}^n \binom{i}{k} f_{i}\Leftrightarrow f_{k}= \sum\limits_{i=0}^n (-1)^{i-k} \binom{i}{k} g_i g k = i = k ∑ n ( k i ) f i ⇔ f k = i = 0 ∑ n ( − 1 ) i − k ( k i ) g i
洛谷P9850
给定n n n m m m f 红色 f_{\text{红色}} f 红色 ( i , j , k , l ) (i,j,k,l) ( i , j , k , l ) f 蓝色 f_{\text{蓝色}} f 蓝色 ( i , j , k , l ) (i,j,k,l) ( i , j , k , l ) ∣ f 红色 − f 蓝色 ∣ |f_{\text{红色}}-f_{\text{蓝色}}| ∣ f 红色 − f 蓝色 ∣ 1 ≤ n ≤ 1 0 5 , 1 ≤ m ≤ 2 × 1 0 5 1\le n \le 10^5,1\le m \le 2\times 10^5 1 ≤ n ≤ 1 0 5 , 1 ≤ m ≤ 2 × 1 0 5
赛时没想出正解(废话都没学二项式反演能做?)
发现蓝色很难受,显然可以考虑以下容斥,但是怎么容斥呢?
但是这咋求啊?暴力枚举直接O ( n 4 ) O(n^4) O ( n 4 )
对于一张存在j j j g i g_i g i i i i ( j i ) \binom{j}{i} ( i j ) f i f_i f i i i i
g i = ∑ j = i ( j i ) f j g_i=\sum\limits_{j=i}\binom{j}{i} f_j g i = j = i ∑ ( i j ) f j
长的就很二项式反演:
f i = ∑ j = i ( j i ) ( − 1 ) j − i g j f_i=\sum\limits_{j=i}\binom{j}{i} (-1)^{j-i} g_j f i = j = i ∑ ( i j ) ( − 1 ) j − i g j
那么∣ f 6 − f 0 ∣ = ∣ g 0 − g 1 + g 2 − g 3 + g 4 − g 5 ∣ |f_6-f_0|=|g_0-g_1+g_2-g_3+g_4-g_5| ∣ f 6 − f 0 ∣ = ∣ g 0 − g 1 + g 2 − g 3 + g 4 − g 5 ∣
g 0 g_0 g 0 ( n 4 ) \dbinom{n}{4} ( 4 n ) g 1 g_1 g 1 ( m 1 ) \dbinom{m}{1} ( 1 m ) ( m 1 ) ( n − 2 2 ) \dbinom{m}{1}\dbinom{n-2}{2} ( 1 m ) ( 2 n − 2 ) g 2 g_2 g 2 如果是一点连两条边,枚举公共点,让后再枚举以该端点出发的两个点,让后再瞎选一个:( n − 3 ) ∑ i = 1 n ( d e g i 2 ) (n-3)\sum\limits_{i=1}^{n}\dbinom{deg_i}{2} ( n − 3 ) i = 1 ∑ n ( 2 d e g i ) d e g i deg_i d e g i i i i 如果没有公共点,正南则反,就是原图任意选2个边减去有公共点的,即:( m 2 ) − ∑ i = 1 n ( d e g i 2 ) \dbinom{m}{2}-\sum\limits_{i=1}^n \dbinom{deg_i}{2} ( 2 m ) − i = 1 ∑ n ( 2 d e g i ) g 3 g_3 g 3 如果三元环,那就枚举剩下一个点为( n − 3 ) C 3 (n-3)C_3 ( n − 3 ) C 3 如果是共用一个顶点,那么很简单直接枚举即可,结果∑ i = 1 n ( n 3 ) \sum\limits_{i=1}^n \binom{n}{3} i = 1 ∑ n ( 3 n ) 如果是链,注意一下要把三元环的三个情况舍去,结果就是∑ ( u , v ) ∈ E ( d e g u − 1 ) ( d e g v − 1 ) − 3 C 3 \sum\limits_{(u,v)\in E}(deg_u-1)(deg_v-1)-3C_3 ( u , v ) ∈ E ∑ ( d e g u − 1 ) ( d e g v − 1 ) − 3 C 3 g 4 g_4 g 4 如果四元环,那不用枚举直接C 4 C_4 C 4 如果三元环出来一个那就是∑ i = 1 n T i ( d e g i − 2 ) \sum\limits_{i=1}^n T_i(deg_i-2) i = 1 ∑ n T i ( d e g i − 2 ) T i T_i T i i i i g 5 g_5 g 5 f 5 = ∑ i = ∈ C 3 ( t i 2 ) f_5=\sum\limits_{i=\in \mathbb{C}_3}\binom{t_i}{2} f 5 = i = ∈ C 3 ∑ ( 2 t i ) C 3 \mathbb{C}_3 C 3 t i t_i t i i i i 做完了,直接公式计算即可,注意瓶颈在三元环和四员化计算,不要超过O ( n 2 ) O(n^2) O ( n 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 #include <bits/stdc++.h> #define pir pair<int, int> #define ll long long using namespace std;constexpr int MN = 1e5 + 15 , MM = 2e5 + 15 ;struct Edge { int u, v; } e[MM]; ll f0, f1, f2, f3, f4, f5; int dg[MN],n,m,top,s[MN],id[MN];ll cp[MN], ce[MM]; vector<int > adj[MN]; vector<pir> G[MN]; ll countthree () { ll ret = 0 ; for (int i = 1 ; i <= n; i++) { for (auto p : G[i]) id[p.first] = p.second; for (auto p : G[i]) { int v = p.first; for (auto pv : G[v]) { int w = pv.first; if (id[w]) { ret++; cp[i]++; cp[v]++; cp[w]++; ce[p.second]++; ce[pv.second]++; ce[id[w]]++; } } } for (auto p : G[i]) id[p.first] = 0 ; } return ret; } ll countfour () { memset (id, 0 , sizeof (id)); ll ret = 0 ; for (int i = 1 ; i <= n; i++) { for (int v : adj[i]) { for (auto p : G[v]) { int w = p.first; if (dg[i] < dg[w] || (dg[i] == dg[w] && i < w)) { ret += id[w]; if (!id[w]) s[++top] = w; id[w]++; } } } for (int j = 1 ; j <= top; j++) id[s[j]] = 0 ; top = 0 ; } return ret; } int main () cin >> n >> m; for (int i = 1 ; i <= m; i++) { cin >> e[i].u >> e[i].v; dg[e[i].u]++; dg[e[i].v]++; adj[e[i].u].push_back (e[i].v); adj[e[i].v].push_back (e[i].u); } for (int i = 1 ; i <= m; i++) { int u = e[i].u, v = e[i].v; if ((dg[u] == dg[v] && u > v) || dg[u] > dg[v]) swap (u, v); G[u].push_back ({v, i}); } ll tri = countthree (); ll quad = countfour (); for (int i = 1 ; i <= n; i++) { f2+=1LL * dg[i] * (dg[i] - 1 ) / 2 * (n - 4 ); f3+=1LL * dg[i] * (dg[i] - 1 ) * (dg[i] - 2 ) / 6 ; f4+=1LL * cp[i] * (dg[i] - 2 ); for (auto p : G[i]) { int v = p.first; f3+=1LL * (dg[i] - 1 ) * (dg[v] - 1 ); } } for (int i = 1 ; i <= m; i++) { f5+=1LL * ce[i] * (ce[i] - 1 ) / 2 ; } f0=(__int128)n * (n - 1 ) * (n - 2 ) * (n - 3 ) / 24 ; f1=1LL * m * (n - 2 ) * (n - 3 ) / 2 ; f2+=1LL * m * (m - 1 ) / 2 ; f3+=tri * (n - 6 ); f4+=quad; cout << abs (f0 - f1 + f2 - f3 + f4 - f5); return 0 ; }
这个定理真的很冷门的……
威尔逊定理给定了判断某个自然是是否是素数的一个充分必要条件 。
对于自然数n > 1 n>1 n > 1 n n n ( n − 1 ) ! ≡ − 1 ( m o d n ) (n-1)! \equiv -1 \pmod n ( n − 1 ) ! ≡ − 1 ( m o d n )
逆定理:若( p − 1 ) ! ≡ − 1 ( m o d p ) (p-1)! \equiv -1 \pmod p ( p − 1 ) ! ≡ − 1 ( m o d p ) p p p 证明?
首先需要说明的是,我们的前提是n > 1 , n ∈ Z n>1,n \in \mathbb{Z} n > 1 , n ∈ Z
我们把非素数分成几类:
非素数 { 4 大于 4 { 完全平方数 非完全平方数 \text{非素数} \begin{cases} 4 \\ \text{大于}4 \begin{cases} \text{完全平方数} \\ \text{非完全平方数} \end{cases} \end{cases} 非素数 ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 4 大于 4 { 完全平方数 非完全平方数
显然这样分类保证不重不漏
当n = 4 n=4 n = 4 ( 4 − 1 ) ! ≡ 2 ( m o d 4 ) (4-1)! \equiv 2 \pmod 4 ( 4 − 1 ) ! ≡ 2 ( m o d 4 )
当n n n p = k 2 p=k^2 p = k 2 p > 4 p>4 p > 4 k > 2 k>2 k > 2
让后我们比较2 k , p 2k,p 2 k , p
2 k − p = 2 k − k 2 = 2 k − k 2 − 1 + 1 = − ( k − 1 ) 2 + 1 < 0 \begin{aligned} 2k-p & = 2k-k^2 \\ & = 2k-k^2-1+1 \\ & = -(k-1)^2+1<0 \end{aligned} 2 k − p = 2 k − k 2 = 2 k − k 2 − 1 + 1 = − ( k − 1 ) 2 + 1 < 0
推论既得
∵ k < p , 2 k < p ∴ ( p − 1 ) ! = 1 × 2 × ⋯ × k × 2 k × ⋯ × ( p − 1 ) = k × 2 k × n = 2 n k 2 = 2 n p ∴ ( p − 1 ) ! ≡ 0 ( m o d p ) \begin{aligned} &\because k<p,2k<p \\ & \therefore (p-1)! \\ & = 1\times 2 \times \dots \times k \times 2k\times \dots \times (p-1) \\ & =k \times 2k \times n \\ & = 2nk^2 \\ & = 2np \\ & \therefore (p-1)! \equiv 0 \pmod p \end{aligned} ∵ k < p , 2 k < p ∴ ( p − 1 ) ! = 1 × 2 × ⋯ × k × 2 k × ⋯ × ( p − 1 ) = k × 2 k × n = 2 n k 2 = 2 n p ∴ ( p − 1 ) ! ≡ 0 ( m o d p )
若p p p p p p a a a b b b a < b a<b a < b 1 < a < b < p 1<a<b<p 1 < a < b < p
显然有:
( p − 1 ) ! = 1 × 2 × ⋯ × a × b × ⋯ × ( p − 1 ) = a × b × n = n a b = n p ∴ ( p − 1 ) ! ≡ 0 ( m o d p ) \begin{aligned} (p-1)! & =1\times 2\times \dots \times a\times b \times \dots \times (p-1) \\ & = a\times b\times n \\ & = nab \\ & =np \\ & \therefore (p-1)! \equiv 0 \pmod p \end{aligned} ( p − 1 ) ! = 1 × 2 × ⋯ × a × b × ⋯ × ( p − 1 ) = a × b × n = n a b = n p ∴ ( p − 1 ) ! ≡ 0 ( m o d p )
当p p p
二次探测定理:对于质数p p p x 2 ≡ 1 ( m o d p ) x^2 \equiv 1 \pmod p x 2 ≡ 1 ( m o d p ) p p p x 1 = 1 , x 2 = p − 1 x_1=1,x_2=p-1 x 1 = 1 , x 2 = p − 1
再对于a ∈ [ 2 , p − 2 ] a\in [2,p-2] a ∈ [ 2 , p − 2 ] a − 1 ∈ [ 2 , p − 2 ] a^{-1} \in [2,p-2] a − 1 ∈ [ 2 , p − 2 ]
a a − 1 ≡ 1 ( m o d p ) aa^{-1} \equiv 1 \pmod p a a − 1 ≡ 1 ( m o d p )
所以必然有p − 3 2 \frac{p-3}{2} 2 p − 3
( p − 2 ) ! ≡ 1 ( m o d p ) (p-2)! \equiv 1 \pmod p ( p − 2 ) ! ≡ 1 ( m o d p )
两边同乘p − 1 p-1 p − 1 ( − 1 + p ) m o d p (-1+p) \mod p ( − 1 + p ) m o d p
( p − 1 ) ! ≡ − 1 ( m o d p ) (p-1)! \equiv -1 \pmod p ( p − 1 ) ! ≡ − 1 ( m o d p )
对于2 ≤ n ≤ 1 0 9 2\le n \le 10^9 2 ≤ n ≤ 1 0 9
( n − 1 ) ! m o d n (n-1)! \mod n ( n − 1 ) ! m o d n
建议看证明。
UVA1434 YAPTCHA
求下列式子答案:
∑ k = 1 n ⌊ ( 3 k + 6 ) ! + 1 3 k + 7 − ⌊ ( 3 k + 6 ! ) 3 k + 7 ⌋ ⌋ \sum\limits_{k=1}^n \lfloor \frac{(3k+6)!+1}{3k+7} -\lfloor \frac{(3k+6!)}{3k+7} \rfloor \rfloor k = 1 ∑ n ⌊ 3 k + 7 ( 3 k + 6 ) ! + 1 − ⌊ 3 k + 7 ( 3 k + 6 ! ) ⌋ ⌋
我们对于上面定理变个形式:
( n − 1 ) ! + 1 ≡ 0 ( m o d n ) (n-1)!+1\equiv 0 \pmod n ( n − 1 ) ! + 1 ≡ 0 ( m o d n )
到这里你回看上面这个式子,是不是直接就秒了。
别急,我们分类讨论:
当k k k ( 3 k + 6 ) ! + 1 3 k + 7 \dfrac{(3k+6)!+1}{3k+7} 3 k + 7 ( 3 k + 6 ) ! + 1 当k k k ( 3 k + 6 ) ! + 1 3 k + 7 \dfrac{(3k+6)!+1}{3k+7} 3 k + 7 ( 3 k + 6 ) ! + 1 源命题转化为,统计素数问题,线性筛即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <bits/stdc++.h> using namespace std;constexpr int MN=3e6 +100 ;int T,cnt[MN];vector<bool > notprime (MN+5 ) ,isprime (MN+15 ) ;vector<int > prime; void shai (int n) for (int i=2 ;i<=n;i++){ if (!notprime[i]){ isprime[i]=1 ; prime.push_back (i); } for (auto p:prime){ if (i*p>n) break ; notprime[i*p]=1 ; if (i%p==0 ) break ; } } } int main () shai (3e6 +15 ); for (int i=1 ;i<=1e6 ;i++){ cnt[i]=cnt[i-1 ]+isprime[3 *i+7 ]; } cin>>T; while (T--) { int x; cin>>x; cout<<cnt[x]<<'\n' ; } return 0 ; }
补天坑
我们能够解决线性同余方程,这很好,我们来解决高级一点的——高次同余方程。
高次同余方程,有a x ≡ b ( m o d p ) a^x \equiv b \pmod p a x ≡ b ( m o d p ) x a ≡ b ( m o d p ) x^a \equiv b \pmod p x a ≡ b ( m o d p ) x x x
问题:
给定整数a , b , p a,b,p a , b , p a , p a,p a , p a x ≡ b ( m o d p ) a^x \equiv b \pmod p a x ≡ b ( m o d p )
因为a , p a,p a , p p p p
当然我们可以暴力枚举x x x x x x O ( φ ( p ) ) O(\varphi(p)) O ( φ ( p ) )
虽然O ( φ ( p ) ) O(\varphi(p)) O ( φ ( p ) )
什么,优雅的暴力?那不就是分块吗。
我们不妨把待求的x x x A A A x = m A − n x=mA-n x = m A − n
a m A − n ≡ b ( m o d p ) a m A ≡ b a n ( m o d p ) \begin{aligned} a^{mA-n} & \equiv b \pmod p \\ a^{mA} & \equiv ba^{n} \pmod p \end{aligned} a m A − n a m A ≡ b ( m o d p ) ≡ b a n ( m o d p )
显然这里的n n n A , m ≤ ⌈ p A ⌉ A,m\le \lceil \frac{p}{A} \rceil A , m ≤ ⌈ A p ⌉
我们考虑暴力枚举每一个n n n b a n m o d p ba^n \mod p b a n m o d p m m m a m A m o d p a^{mA} \mod p a m A m o d p
枚举n n n O ( A ) O(A) O ( A ) m m m O ( p A ) O(\frac{p}{A}) O ( A p )
注意到A + n A A+\frac{n}{A} A + A n A = n A=\sqrt{n} A = n O ( n ) O(\sqrt{n}) O ( n )
所以为什么是大步小步呢,你看a n a^n a n n n n a a a a m A a^{mA} a m A a A a^A a A
代码如下,实现因为用了 map 所以多一个log \log log
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 map<int ,int > mp; int BSGS (int a,int b,int p) mp.clear (); b%=p; int t=sqrt (p)+1 ; for (int j=0 ;j<t;j++){ int val=(long long )b*qpow (a,j,p)%p; mp[val]=j; } a=qpow (a,t,p); if (a==0 ) return b==0 ?1 :-1 ; for (int i=0 ;i<t;i++){ int val=qpow (a,i,p); int j=mp.find (val)==mp.end ()?-1 :mp[val]; if (j>=0 &&i*t-j>=0 ) return i*t-j; } return -1 ; }
就和拓展中国剩余定理一样,我们这里的拓展就是不互质的情况下,那怎么做?
注意到,我们当然互质不能做(废话 ),我们考虑怎么改写。
咱们可以换成求解线性同余方程的形式,变形为:
a x + k p = n a^x +kp =n a x + k p = n
当gcd ( a , n ) ∣ n \gcd(a,n)|n g cd( a , n ) ∣ n
由特殊解推一般解公式(还是裴蜀定理那里)得:
a x − 1 ⋅ a d + k ⋅ p d = n d a^{x-1} \cdot \frac{a}{d} + k \cdot \frac{p}{d}=\frac{n}{d} a x − 1 ⋅ d a + k ⋅ d p = d n
考虑重新传参,一直递归直到gcd ( a , p ) = 1 \gcd(a,p)=1 g cd( a , p ) = 1
不妨设递归了c n t cnt c n t d d d d ′ d' d ′
原式即为:
a x − c n t ⋅ a c n t d ′ ≡ n d ′ ( m o d p d ′ ) a^{x-cnt} \cdot \frac{a^{cnt}}{d'} \equiv \frac{n}{d'} \pmod{\frac{p}{d'}} a x − c n t ⋅ d ′ a c n t ≡ d ′ n ( m o d d ′ p )
此时互质,BSGS即可,当然结果要加上c n t cnt c n t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 int qpow (int a,int b,int MOD) int ret=1 ; while (b){ if (b&1 ){ ret=ret*a%MOD; } a=a*a%MOD; b>>=1 ; } return ret; } int exgcd (int a,int b,int &x,int &y) if (!b){ x=1 ,y=0 ; return a; } int d=exgcd (b,a%b,y,x); y-=a/b*x; return d; } int BSGS (int a,int b,int p) mp.clear (); b%=p; int t=sqrt (p)+1 ; for (int j=0 ;j<t;j++){ int val=b*qpow (a,j,p)%p; mp[val]=j; } a=qpow (a,t,p); if (a==0 ) return b==0 ?1 :-1 ; for (int i=0 ;i<=t;i++){ int val=qpow (a,i,p); int j=mp.find (val)==mp.end ()?-1 :mp[val]; if (j>=0 &&i*t-j>=0 ) return i*t-j; } return -1 ; } int exBSGS (int a,int b,int p) a%=p,b%=p; if (b==1 ||p==1 ) return 0 ; int gcdd,d=1 ,cnt=0 ,x,y; while ((gcdd=exgcd (a,p,x,y))^1 ){ if (b%gcdd) return -1 ; b/=gcdd,p/=gcdd; cnt++; d=1ll *d*(a/gcdd)%p; if (d==b) return cnt; } exgcd (d,p,x,y); int inv=(x%p+p)%p; b=1ll *b*inv%p; int ans=BSGS (a,b,p); if (ans==-1 ) return -1 ; else return ans+cnt; }
的所有因数可以被分成两块,即和 。只需要把里的数遍历一遍,再根据除法就可以找出至少两个因数了。这个方法的时间复杂度为 。
。这两点保证了,当循环进行到
的一个因子,且不被任何小于
的因子。当循环进行到
的因子,故而有
的因子。当对
的一个因子。
,则必然存在
,满足
不可能作为循环中的某个
时,
的
也不可能在循环结束后加入,因为循环退出的条件是
的
。
的素因子必然出现在
是
的一个素因子,但并没有出现在
不可能是循环中出现过的
,而退出循环后的
整除
,必会在最后加入