0.前言

你需要的必备芝士：

  1. 图的存储与遍历。
  2. DFS序。
  3. 线段树的基础应用。
  4. LCA的概念与性质。

准备好了？Let’s GO!

1.重链剖分

什么是树链剖分？他是干什么的？

树链剖分，字面意思就是将树剖成一条一条链，让后我们利用这些链来维护树上路径的信息。

那我们举个例子吧。

nn 个点的树，有mm 次操作，每一次操作将树上x→yx\rightarrow y 的路径都加11 的权值 ，求树所有节点的权值之和。

不难发现树上差分。直接差分做一做就可以了，不知道的可以看我的博客。

但是如果我想求路径的值呢？

nn 个点的树，有mm 次操作，每一次操作将树上x→yx\rightarrow y 的路径都加11 的权值 。
给定qq 次询问，询问最短路径u→vu\rightarrow v上的权值之和

这个时候问题就不一样了，仅靠差分的话复杂度会炸成O(nq)O(nq)，怎么办？如果这个问题我们不放到树上，我们就是一个数组的操作，很简单对吧，线段树和树状数组都可以轻轻松松的做到，但是放到树上怎么做我们肯定是不会的。接下来我们要介绍树链剖分是如何做到这一点的。

树链剖分，就是把树剖分成若干条链，使其组合成线性结构，让后用数据结构维护链的信息。 ——OI Wiki

说人话就是：把一颗树拆成若干个不相交的链，让后用数据结构维护链的信息。

说到底为什么我们非要拆成链来维护呢？回忆树上差分，差分本质上我们只能在一个线性结构比如说数组上维护，但是放在树上我们不会做。但是我们可以把一条路径在LCA处劈成2半，分别进行拆分，如下图。我们将这颗树的3→63\rightarrow 6的路径都加上11 。我们拆成了3→2,5→63 \rightarrow 2,5\rightarrow 6，2条线性的链，这样我们进行差分就十分方便了。

让后差分的结果如下：

而对于路径信息的维护也很好说，就像差分拆成链的思想一样，我们也用链来去维护。上文我们提到了如果我们不放到树上就很好做，只需要用线段树来去维护就可以了，问题在于树不是像数组。但是我们可以利用拆链的思想，把它拆成一条一条链，这样不就类似于数组了吗，让后我们维护数组的信息，就可以了。

现在问题在于我们怎么把树拆成一条一条链？而且这个链应该怎么拆才能保证我的复杂度不会炸掉？

我们有2种方法，一种叫重链剖分，一种叫长链剖分。我们先讲重链剖分。

先来几个概念，别怕会有图辅助理解的：

  • 重儿子（hsonhson数组记录）：该节点子树中，节点个数最多的子树的根节点，即为该节点的重儿子。

对于上面的树结构，节点11 的重儿子就是22 因为节点个数有4个，而对于节点22 的重儿子是55 ，因为有2个比3号点要大。而对于3，6，5号点没有重儿子，因为他们是叶子节点。

  • 重边：连接该节点与它重儿子的边

就像上面，例如1→2,2→51\rightarrow 2,2\rightarrow 5。

  • 重链（toptop数组记录顶端）：由一系列重边相连得到的链。特别的，落单的节点也是重链。
  • 轻链：由一系列非重边相连得到的链。

借用OI-Wiki的图：

这样就不难得到拆树的方法。对于每个节点我们只需要找出它的重儿子，让后就可以根据这些信息拆成许多许多链了。

话是这么说但是到底咋求？

我们要分成2次来DFS进行求，我们需要维护如下信息。

名称变量名含义维护方式
子树大小sizsiz子树节点的数量，用于判断轻重儿子自底向上统计（第一次DFS）
重儿子hsonhson一个节点的重儿子，若无默认为0用子树大小sizsiz计算取siz[v]siz[v]最大的vv（第一次DFS）
节点深度depdep节点在树的深度自上向下计算（第一次DFS）
节点的父亲fafa父亲节点字面意思维护即可（第一次DFS）
重链toptop一条重链的顶端节点，其中top[u]top[u]表示uu号点所在链的顶端遍历重儿子赋值即可（第二次DFS）
按照链遍历的DFS序idid重链优先遍历的DFS序字面意思先遍历重边在遍历轻边（第二次DFS）

根据这个表，我们能够很轻松的设计出第一个DFS函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void dfs1(int u,int pre){// u号节点，父亲节点是pre
    dep[u]=dep[pre]+1;// 深度
    siz[u]=1;// 子树大小
    fa[u]=pre;// 父亲
    int maxp=-1;//初始化最大sizv为-1
    for(auto v:adj[u]){
        if(v==pre) continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(maxp<siz[v]){// 更新hson
            maxp=siz[v];
            hson[u]=v;
        }
    }
}

而对于第二次的DFS函数，也是很好设计。

1
2
3
4
5
6
7
8
9
10
void dfs2(int u,int ltop){
    id[u]=++cnt;// 设置id，因为我们优先遍历重链所以是重链优先的dfn序
    top[u]=ltop;//节点u所在链的顶端
    if(!hson[u]) return;//如果没有重儿子显然叶子节点
    dfs2(hson[u],ltop);// 先剖重链
    for(auto v:adj[u]){
        if(v==fa[u]||v==hson[u]) continue; // 别忘了排除重儿子！
        dfs2(v,v);//处理轻链
    }
}

toptop 还好说，为什么要设计idid ？别忘了，我们最终是要用线段树等数据结构来进行维护，这样维护的话一条链在idid 上是排成一个连续区间（即DFS序是连续的），这样就方便了。

我们建一颗支持区间加的线段树，让后我们考虑怎么维护树上的操作。

回顾上面的图，我们其实对于路径来说就是根据LCA拆成2条链进行操作。

问题来了，怎么求LCA？

一个很显然的想法就是倍增求LCA，但是我跟你说这个也可以同时求出LCA呢？

我们对上面的图进行小小的改编，并进行重链剖分。对于6号点也是可以作为最长重链的终点，不过链不能分叉。

我们不妨借鉴倍增求LCA的思想：2个节点借助fafa数组跳到同一个节点。对于重链剖分来说，就是在不同重链的节点，我们让他们不断的跳直到处于同一重链（如果一开始就是同一重链，想一想还用跳吗？）。还记得我们求的toptop 数组吗？这个就是替代倍增fafa的关键。我们直接跳到链的顶端，这样就可以有像倍增跳fafa一样的效果了！当然和倍增算法一样，我们让dep[top[x]],dep[top[y]]dep[top[x]],dep[top[y]]中深度大的往上跳。

跳到最后会出现一个情况，虽然x,yx,y在一条链上但不一定重合，此时lcalca就是深度小的节点。

不难有lcalca函数：

1
2
3
4
5
6
7
8
9
int lca(int x,int y){
    while(top[x]!=top[y]){//如果不在一条链就继续跳
        if(dep[top[x]]<dep[top[y]]){// 优先跳深度大的
            swap(x,y);
        }
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;// 深度小的即为LCA
}

等会，时间复杂度多少？这个我们待会再说。

LCA求完那就都好说，直接LCA维护就可以了。

例如路径加：

1
2
3
4
5
6
7
8
9
10
void addchain(int x,int y,ll k){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        sg.add(1,id[top[x]],id[x],k);// x跳的过程中我们就要加上权值，顺序不要搞反了。
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    sg.add(1,id[x],id[y],k);
    // 处理路径LCA->y的权值，因为LCA与y已经在一条链上所以可以直接加
}

有的人会说，你这个跳LCA的时候会更换x,yx,y，难道不会重复加吗？这种问题的解法可以自己模拟一遍LCA的跳法，看看是否会重复加区间，显然是不会的。

到这里前面2个问题就解决完毕了，但是我还有一个问题。如果我要加子树的权值呢。

给定节点uu，将uu的子树内权值都加上wiw_i。特别的，叶子节点的子树就是节点本身。

我们思考一个问题，重链优先遍历在子树内的DFS序是连续的吗？

显然是连续的，这里不再证明。

那么就好说了，直接对[id[x],id[x]+siz[x]−1][id[x],id[x]+siz[x]-1]维护即可。减一是因为sizsiz包含自己xx。

1
2
3
4
5
6
7
void addchild(int x,ll k){ //加
    sg.add(1,id[x],id[x]+siz[x]-1,k);
}

ll querychild(int x){ // 查
    return sg.query(1,id[x],id[x]+siz[x]-1)%MOD;
}

所以时间复杂度到底是多少？

有一个性质：向下经过一条 轻边 时，所在子树的大小至少会除以二。

这个是根据性质来说的，那么不难发现，我们拆LCA路径的做法只需要最多走O(log⁡n)O(\log n)次，树上每条路径最多可以划分成不超过O(log⁡n)O(\log n)条重链。

来做题，P3884:

nn个节点的树，根节点为RR，树节点有初始权值wiw_i。mm次操作:
1 x y z，表示将树从xx 到yy 结点最短路径上所有节点的值都加上zz。
2 x y，表示求树从xx 到yy 结点最短路径上所有节点的值之和。
3 x z，表示将以xx 为根节点的子树内所有节点值都加上zz。
4 x 表示求以xx 为根节点的子树内所有节点值之和。
数据对给定的模数PP取模。
1≤n,m≤105,1≤R≤n,1≤P≤2301\le n,m \le 10^5,1\le R \le n,1\le P \le 2^{30}

照着写就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=5e5+15;
int n,m,rt,MOD,cnt,dep[MN],siz[MN],fa[MN],id[MN],hson[MN],top[MN];
ll w[MN];
vector<int> adj[MN];
struct segtree{
    #define ls p<<1
    #define rs p<<1|1

    struct{
        int l,r;
        ll sum,add;
    }t[MN<<2];

    void pushup(int p){
        t[p].sum=(t[ls].sum+t[rs].sum)%MOD;
    }

    void build(int p,int l,int r){
        t[p].l=l;
        t[p].r=r;
        if(l==r){
            t[p].sum=0;
            return;
        }
        int mid=(l+r)>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
        pushup(p);
    }

    void pushdown(int p){
        if(t[p].add){
            t[ls].sum=(t[ls].sum+(t[ls].r-t[ls].l+1)*t[p].add)%MOD;
            t[rs].sum=(t[rs].sum+(t[rs].r-t[rs].l+1)*t[p].add)%MOD;

            t[ls].add=(t[ls].add+t[p].add)%MOD;
            t[rs].add=(t[rs].add+t[p].add)%MOD;

            t[p].add=0;
        }
    }

    void add(int p,int fl,int fr,ll k){
        if(t[p].l>=fl&&t[p].r<=fr){
            t[p].add=(t[p].add+k)%MOD;
            t[p].sum=(t[p].sum+(t[p].r-t[p].l+1)*k)%MOD;
            return;
        }
        pushdown(p);
        int mid=(t[p].l+t[p].r)>>1;
        if(mid>=fl) add(ls,fl,fr,k);
        if(mid<fr) add(rs,fl,fr,k);
        pushup(p);
    }

    ll query(int p,int fl,int fr){
        if(t[p].l>=fl&&t[p].r<=fr){
            return t[p].sum;
        }
        pushdown(p);
        int mid=(t[p].l+t[p].r)>>1;
        ll ret=0;
        if(mid>=fl) ret=(ret+query(ls,fl,fr))%MOD;
        if(mid<fr) ret=(ret+query(rs,fl,fr))%MOD;
        return ret;
    }

    #undef ls
    #undef rs
}sg;

void dfs1(int u,int pre){
    dep[u]=dep[pre]+1;
    siz[u]=1;
    fa[u]=pre;
    int maxp=-1;
    for(auto v:adj[u]){
        if(v==pre) continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(maxp<siz[v]){
            maxp=siz[v];
            hson[u]=v;
        }
    }
}

void dfs2(int u,int ltop){
    id[u]=++cnt;
    top[u]=ltop;
    if(w[u]!=0){
        sg.add(1,id[u],id[u],w[u]);
    }
    if(!hson[u]) return;
    dfs2(hson[u],ltop);
    for(auto v:adj[u]){
        if(v==fa[u]||v==hson[u]) continue;
        dfs2(v,v);
    }
}

void addchain(int x,int y,ll k){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        sg.add(1,id[top[x]],id[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    sg.add(1,id[x],id[y],k);
}

ll querychain(int x,int y){
    ll ret=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        ret=(ret+sg.query(1,id[top[x]],id[x]))%MOD;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    ret=(ret+sg.query(1,id[x],id[y]))%MOD;
    return ret;
}

void addchild(int x,ll k){
    sg.add(1,id[x],id[x]+siz[x]-1,k);
}

ll querychild(int x){
    return sg.query(1,id[x],id[x]+siz[x]-1)%MOD;
}

int main(){
    // freopen("ans.in","r",stdin);
    cin>>n>>m>>rt>>MOD;
    for(int i=1;i<=n;i++){
        cin>>w[i];
    }
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    sg.build(1,1,n);
    dfs1(rt,0);
    dfs2(rt,rt);
    while(m--){
        int op,x,y;
        ll z;
        cin>>op>>x;
        if(op==1){
            cin>>y>>z;
            addchain(x,y,z%MOD);
        }
        if(op==2){
            cin>>y;
            cout<<querychain(x,y)%MOD<<'\n';
        }
        if(op==3){
            cin>>z;
            addchild(x,z);
        }
        if(op==4){
            cout<<querychild(x)%MOD<<'\n';
        }
    }
    return 0;
}

1.1 例题

CF1555F:

有一含 n 个点的带权无向图。
一个简单环被定义为图上一没有重复顶点的环。令这样的一个环的权重为它环上所有边的权值的异或和。
若一个图中全部简单环的权重都是 1 ，那么我们称这个图为好图，而一个图若不是好图，那么这个图则是坏图。
最开始，图是空的。接着会有 q 个询问。每个询问为以下格式：
u v x — 若不会使图变成坏图，则在点 u 与点 v 间加一条权值为 x 的边。
对于每一个询问输出到底加不加这条边。

这个不是图论吗？和树上路径有什么关系？

针对环的问题我们有一个套路就是：离线造生成树。

环用并查集判断联通性。

我们考虑什么边能加进来，第一类就是生成树本来的边是可以加；第二类就是这条非树边加入所构成的环不与其他的任何环相交，并且路径异或和为1即可。

非树边的加入我们可以考虑转化成线段树最大值/和来维护，我们把在环上的边赋值为1，不再的赋值为0，可以加入的条件就是路径上所有边权值都是0，考虑树剖。路径异或和为1考虑树上前缀异或和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
#include<bits/stdc++.h>
using namespace std;
const int MN=5e5+15,MQ=5e5+15;
int n,m,cnt,id[MN],sum[MN],hson[MN],pre[MN],top[MN],dep[MN],siz[MN],fa[MN];
bool isok[MN];
struct qedge{
    int u,v,w;
}q[MQ];
struct edge{
    int v,w;
};
vector<edge> adj[MN];

struct segtree{
    #define ls p<<1
    #define rs p<<1|1
    struct{
        int l,r,val,cov;
    }t[MN<<2];

    void pushup(int p){
        t[p].val=max(t[ls].val,t[rs].val);
    }

    void build(int p,int l,int r){
        t[p].l=l;
        t[p].r=r;
        t[p].cov=-1;
        if(l==r){
            t[p].val=0;
            return;
        }
        int mid=(l+r)>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
        pushup(p);
    }

    void pushdown(int p){
        if(t[p].cov!=-1){
            t[ls].val=t[ls].cov=t[rs].val=t[rs].cov=t[p].cov;
            t[p].cov=-1;
        }
    }

    void update(int p,int fl,int fr,int k){
        if(t[p].l>=fl&&t[p].r<=fr){
            t[p].val=t[p].cov=k;
            return;
        }
        pushdown(p);
        int mid=(t[p].l+t[p].r)>>1;
        if(mid>=fl) update(ls,fl,fr,k);
        if(mid<fr) update(rs,fl,fr,k);
        pushup(p);
    }

    int queryone(int p,int fl,int fr){
        if(t[p].l>=fl&&t[p].r<=fr){
            return t[p].val;
        }
        pushdown(p);
        int mid=(t[p].l+t[p].r>>1);
        if(mid>=fl&&queryone(ls,fl,fr)) return 1;
        if(mid<fr&&queryone(rs,fl,fr)) return 1;
        return 0;
    }

    #undef ls
    #undef rs
}sg;

void initpre(){
    for(int i=1;i<=n;i++) pre[i]=i;
}

void dfs1(int u,int pree){
    dep[u]=dep[pree]+1;
    siz[u]=1;
    fa[u]=pree;
    int maxp=-1;
    for(auto e:adj[u]){
        int v=e.v,w=e.w;
        if(v==pree) continue;
        sum[v]=sum[u]^w;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(maxp<siz[v]){
            maxp=siz[v];
            hson[u]=v;
        }
    }
}

void dfs2(int u,int ltop){
    id[u]=++cnt;
    top[u]=ltop;
    if(!hson[u]) return;
    dfs2(hson[u],ltop);
    for(auto e:adj[u]){
        int v=e.v,w=e.w;
        if(v==hson[u]||v==fa[u]) continue;
        dfs2(v,v);
    }
}

int root(int x){
    if(pre[x]==x) return x;
    else return pre[x]=root(pre[x]);
}

int ask(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        if(sg.queryone(1,id[top[x]],id[x])) return 1;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    if(id[x]+1<=id[y]&&sg.queryone(1,id[x]+1,id[y])) return 1;
    return 0;
}

void modify(int x,int y,int k){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        sg.update(1,id[top[x]],id[x],1);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    if(id[x]+1<=id[y])sg.update(1,id[x]+1,id[y],k);
}

int main(){
    //freopen("ans.in","r",stdin);
    cin>>n>>m;
    sg.build(1,1,MQ);
    initpre();
    for(int i=1;i<=m;i++){
        cin>>q[i].u>>q[i].v>>q[i].w;
        int ru=root(q[i].u),rv=root(q[i].v);
        if(ru!=rv){
            isok[i]=1;
            // cout<<q[i].u<<" "<<q[i].v<<" "<<q[i].w<<'\n';
            adj[q[i].u].push_back({q[i].v,q[i].w});
            adj[q[i].v].push_back({q[i].u,q[i].w});
            pre[rv]=ru;
        }
    }
    for(int i=1;i<=n;i++){
        if(!dep[i]){
            dfs1(i,0);
            dfs2(i,i);
        }
    }
    //cout<<cnt<<'\n';
    for(int i=1;i<=m;i++){
        if(isok[i]) cout<<"YES\n";
        else{
            if(!(sum[q[i].u]^sum[q[i].v]^q[i].w)) cout<<"NO\n";
            else{
                if(ask(q[i].u,q[i].v)){
                    cout<<"NO\n";
                }else{
                    modify(q[i].u,q[i].v,1);
                    cout<<"YES\n";
                }
            }
        }
    }
    return 0;
}

1.2 LCA

根据我们上面说的求就可以了，这里给出一个模板。

时间复杂度预处理O(n)O(n)，查询O(log⁡n)O(\log n)，常数小，代码简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
constexpr int MN=5e5+15;
int n,m,s;
int hson[MN],dep[MN],top[MN],fa[MN],siz[MN];
vector<int> adj[MN];

void dfs1(int u,int pre){
    siz[u]=1;
    fa[u]=pre;
    dep[u]=dep[pre]+1;
    int maxp=-1;
    for(auto v:adj[u]){
        if(v==pre) continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(maxp<siz[v]){
            hson[u]=v;
            maxp=siz[v];
        }
    }
}

void dfs2(int u,int ltop){
    top[u]=ltop;
    if(!hson[u]) return;
    dfs2(hson[u],ltop);
    for(auto v:adj[u]){
        if(v==fa[u]||v==hson[u]){
            continue;
        }
        dfs2(v,v);
    }
}

int lca(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]){
            swap(x,y);
        }
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}

int main(){
    cin>>n>>m>>s;
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs1(s,0);
    dfs2(s,s);
    for(int i=1;i<=m;i++){
        int u,v;
        cin>>u>>v;
        cout<<lca(u,v)<<'\n';
    }
    return 0;
}

2.长链剖分

2.1 介绍

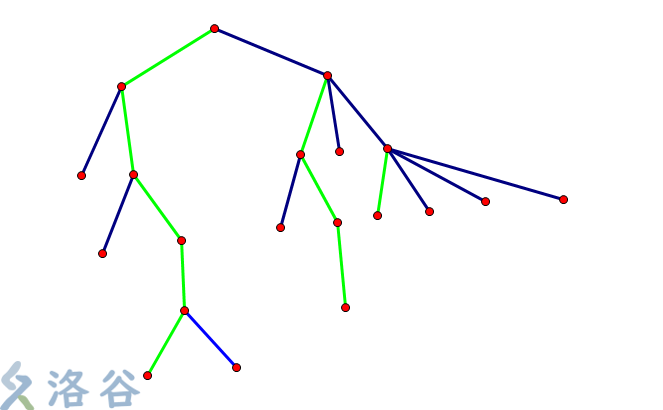
长链剖分和重链剖分不一样的一点，前者以子树深度最大的儿子为重儿子，而后者以子树大小最大的儿子为重儿子。

举个例子，例如下面这棵树，绿色的边就是长链：

我们定义一个节点和它的长儿子节点相连的边（就是上图绿色的边）为实边，其他为虚边。

以下是代码实现，和重链剖分差不太多：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
namespace Tree{
    int dep[MN],fa[MN],mxdep[MN],htop[MN],len[MN],hson[MN];
    void dfs1(int u,int pre){
        fa[u]=pre;
        dep[u]=mxdep[u]=dep[pre]+1;
        for(int i=hd[u];i;i=nxt[i]){
            int v=to[i];
            if(v==pre) continue;
            dfs1(v,u);
            if(mxdep[u]<mxdep[v]) mxdep[u]=mxdep[v],hson[u]=v;
        }
        len[u]=mxdep[u]-dep[u]+1;
    }
    void dfs2(int u,int ltop){
        htop[u]=ltop;
        if(!hson[u]){return;}
        dfs2(hson[u],ltop);
        for(int i=hd[u];i;i=nxt[i]){
            int v=to[i];
            if(v==fa[u]||v==hson[u]) continue;
            dfs2(v,v);
        }
    }
}using namespace Tree;

2.2 长链剖分的性质

长链剖分有如下的性质：

  • 从根节点到任意叶子结点经过的轻边条数不超过n\sqrt{n}，比重链剖分的log⁡n\log n 有点劣。
  • 一个节点的kk 级祖先所在长链长度一定不小于kk。
  • 每个节点所在长链末端为其子树内最深节点。
  • 选一个节点能覆盖它到根的所有节点。选kk 个节点，覆盖的最多节点数就是前kk 条长链长度之和，选择的节点即kk 条长链末端。

2.3 应用

2.3.1 树上 k 级祖先

首先O(nlog⁡n)O(n\log n) 的倍增预处理求出每个节点uu 的2k2^k 级祖先，以及对于每一条长链，从长链向上向下ii 步分别能走到哪个节点，其中ii 不超过长链深度。此外预处理每个数在二进制下的最高位（即⌊log⁡2i⌋\lfloor \log_2 i \rfloor，不想预处理的可以用 __lg 函数）lgilg_i。预处理为O(nlog⁡n)+O(n)+O(n)O(n \log n)+O(n)+O(n)。

一次查询(u,k)(u,k)，首先跳到uu 的2lgk2^{lg_k} 级祖先fafa，由于我们与处理了从fafa 所在长链顶端tt 向上/下走不超过链长步分别到哪个节点，故不难直接查询，故查询时间复杂度为O(1)O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<bits/stdc++.h>
#define ui unsigned int
using namespace std;
constexpr int MN=1e6+15;
int n,q,rt,hb[MN];
ui s;
long long ans;
vector<int> adj[MN];

namespace Tree{
    int dep[MN],mxdep[MN],fa[21][MN],hson[MN],htop[MN];
    vector<int> up[MN],dw[MN];

    void dfs1(int u,int pree){
        dep[u]=mxdep[u]=dep[pree]+1;
        fa[0][u]=pree;
        for(int i=1;i<=20;i++){
            fa[i][u]=fa[i-1][fa[i-1][u]];
        }
        for(auto v:adj[u]){
            if(v==pree) continue;
            dfs1(v,u);
            if(mxdep[v]>mxdep[u]){
                mxdep[u]=mxdep[v];
                hson[u]=v;
            }
        }
    }

    void dfs2(int u,int ltop){
        htop[u]=ltop;
        if(u==ltop){
            for(int i=0,it=u;i<=mxdep[u]-dep[u];i++){
                up[u].push_back(it),it=fa[0][it];
            }
            for(int i=0,it=u;i<=mxdep[u]-dep[u];i++){
                dw[u].push_back(it),it=hson[it];
            }
        }
        if(hson[u]) dfs2(hson[u],ltop);
        for(auto v:adj[u]){
            if(v==fa[0][u]||v==hson[u]) continue;
            dfs2(v,v);
        }
    }

    int query(int x,int k){
        if(!k) return x;
        x=fa[__lg(k)][x];
        k-=1<<(__lg(k));
        k-=dep[x]-dep[htop[x]];
        x=htop[x];
        return k>=0?up[x][k]:dw[x][-k];
    }

}using namespace Tree;

ui get(ui x){
	x ^= x << 13;
	x ^= x >> 17;
	x ^= x << 5;
	return s = x; 
}

signed main(){
    read(n,q,s);
    for(int i=1;i<=n;i++){
        int faa;
        read(faa);
        if(!faa){
            rt=i;
            continue;
        }
        adj[faa].push_back(i);
        adj[i].push_back(faa);
    }
    dfs1(rt,0);
    dfs2(rt,rt);
    int lst=0;
    for(int i=1;i<=q;i++){
        int x,k;
        x=(get(s)^lst)%n+1;
        k=(get(s)^lst)%dep[x];
        lst=query(x,k);
        ans^=1ll*i*(lst);
    }
    cout<<ans;
    return 0;
}

2.3.2 长链剖分优化 DP

长链剖分的价值主要体现在于能够优化树上有关深度的 DP，如果子树内每个深度仅对应一个信息，我们就可以用长链剖分优化。

一般形式为：f(i,j)f(i,j) 表示以ii 为根的子树内，深度为jj 节点的贡献。

下面以一道例题来看：

CF1009F

先考虑dd 怎么求，有一个显然的转移方程：

d(i,j)=∑x∈son(i)d(x,j−1)d(i,j)=\sum_{x\in son(i)} d(x,j-1)

初始化f(i,0)=1f(i,0)=1。

然而是O(n2)O(n^2) 的，无法承受，注意到这个信息子树深度有且仅对应顶点个数这一个信息而非具体是哪些顶点，因此子树内深度相同的点等价。考虑长链剖分优化 DP。

具体的，类似于 DSU on Tree，我们直接继承重儿子的答案，让后将所有轻儿子的答案合并过来，因为每个点uu 最多合并一次，即合并uu 所在重链顶端toptop 的父亲fafa 与tt 时，uu 所包含的信息就和dfad_{fa} 在depu−depfadep_u -dep_{fa} 处的信息融为了一体，相当于点uu 直接消失了，时间复杂时优秀的O(n)O(n)。

具体实现上，如何继承重儿子的 DP 值，一个解决方案就是用指针申请内存，对于一条重链，共用一个大小为其长度的数组。这同时解决了上述两个问题。实现时需要特别注意开足空间，并弄清转移方向。

另一个方法就是 vector，不过通用性没那么好，这里就不再赘述了。

2.4 例题

CF1009F

提交记录

P4292 重建计划

直接 01 分数规划上来就是一个二分答案，让后将减掉midmid 后问题转化为求一个长度在[L,U][L,U] 之间且边权非负的路径。考虑 DP，设f(i,j)f(i,j) 表示ii 子树内深度为jj 的最大路径权值和，转移是显然的，也容易看出来我们求的是最大值，每一个长度只会贡献唯一一个信息。

考虑长链剖分优化 DP，合并子树的时先遍历轻儿子的答案，这个需要我们求重链的一段区间 dp 值的最大值，若轻儿子对应位置比重儿子更大就修改，所以我们还需要区间单点修改，考虑线段树维护。线段树上我们可以通过给每一个节点赋一个 dfs 序，那么线段树上对应的位置就是(dfn[x]+j)(dfn[x]+j)（jj 为 dp 里面的），时间复杂度O(nlog⁡2n)O(n \log^2 n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
#include<bits/stdc++.h>
#define double long double
#define int long long
using namespace std;
constexpr int MN=1e5+15;
constexpr double eps=1e-6;
struct Edge{
    int v,w;
};
int n,L,R;
double tmp[MN],V;
vector<Edge> adj[MN];

struct Segment{
#define ls p<<1
#define rs p<<1|1

    struct Node{
        int l,r;
        double val;
    }t[MN<<2];

    void pushup(int p){
        t[p].val=max(t[ls].val,t[rs].val);
    }

    void build(int p,int l,int r){
        t[p].l=l;
        t[p].r=r;
        t[p].val=-1e18;
        if(l==r) return;
        int mid=(l+r)>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
    }

    void modify(int p,int pos,double k){
        if(t[p].l==t[p].r){
            t[p].val=max(t[p].val,k);
            return;
        }
        int mid=(t[p].l+t[p].r)>>1;
        if(mid>=pos) modify(ls,pos,k);
        else modify(rs,pos,k);
        pushup(p);
    }

    double query(int p,int fl,int fr){
        if(fl>fr) return -1e18;
        if(t[p].l>=fl&&t[p].r<=fr){
            return t[p].val;
        }
        int mid=(t[p].l+t[p].r)>>1;
        double ret=-1e18;
        if(mid>=fl) ret=query(ls,fl,fr);
        if(mid<fr) ret=max(ret,query(rs,fl,fr));
        return ret;
    }
#undef ls
#undef rs
}sg;

namespace Tree{
    int htop[MN],hson[MN],dep[MN],mxdep[MN],val[MN],len[MN],fa[MN],dfn[MN],dtot;
    double dis[MN],ret;

    void dfs1(int u,int pre){
        fa[u]=pre;
        dep[u]=mxdep[u]=dep[pre]+1;
        for(auto e:adj[u]){
            int v=e.v,w=e.w;
            if(v==pre) continue;
            dfs1(v,u);
            if(mxdep[u]<mxdep[v]){
                mxdep[u]=mxdep[v];
                hson[u]=v;
                val[v]=w;
            }
        }
        len[u]=mxdep[u]-dep[u];
    }

    void dfs2(int u,int ltop){
        dfn[u]=++dtot;
        if(hson[u]) dfs2(hson[u],ltop);
        for(auto e:adj[u]){
            int v=e.v,w=e.w;
            if(v==fa[u]||v==hson[u]) continue;
            dfs2(v,v);
        }
    }

    void dfs3(int u,int pre){
        sg.modify(1,dfn[u],dis[u]);
        if(hson[u]){
            dis[hson[u]]=dis[u]+val[hson[u]]-V;
            dfs3(hson[u],u);
        }
        for(auto e:adj[u]){
            int v=e.v,w=e.w;
            if(v==fa[u]||v==hson[u]) continue;
            dis[v]=dis[u]+e.w-V;
            dfs3(v,u);
            for(int i=1;i<=len[v]+1;i++){
                tmp[i]=sg.query(1,dfn[v]+i-1,dfn[v]+i-1);
            }
            for(int i=1;i<=min(len[v]+1,R);i++){
                ret=max(ret,tmp[i]+sg.query(1,dfn[u]+L-i,min(dfn[u]+R-i,dfn[u]+len[u]))-2*dis[u]);
            }
            for(int i=1;i<=len[v]+1;i++){
                sg.modify(1,dfn[u]+i,tmp[i]);
            }
        }
        ret=max(ret,sg.query(1,dfn[u]+L,min(dfn[u]+R,dfn[u]+len[u]))-dis[u]);
    }
}using namespace Tree;

bool check(double x){
    sg.build(1,1,n);
    V=x,ret=-1e18;
    dfs3(1,0);
    return ret>=0;
}

signed main(){
    cin>>n>>L>>R;
    for(int i=1;i<n;i++){
        int u,v,w;
        cin>>u>>v>>w;
        adj[u].push_back({v,w});
        adj[v].push_back({u,w});
    }
    dfs1(1,0);
    dfs2(1,1);
    double l=0,r=1e7;
    while(r-l>eps){
        double mid=(l+r)/2;
        if(check(mid)) l=mid;
        else r=mid;
    }
    cout<<fixed<<setprecision(3)<<l;

    return 0;
}

P5904 HOT-Hotels

手摸样例启示我们在三个点的 LCA 处统计贡献，直接统计的话虽然解决了三个点到 LCA 距离相等的情况，但是没有统计一个点离 LCA 远，另外两个点离 LCA 距离近一点的形态。考虑用 DP 统计答案，设f(i,j)f(i,j) 表示ii 子树内，距离为jj 的节点个数，让后再来一个转台处理离远一点的信息，设g(i,j)g(i,j) 表示ii 子树内来一个长度为jj 的链凑成 3 元组的数量。ff 的转移时显然的，而gg 不太好从儿子转移过来。

遇到这种不太好从儿子转移到父亲的节点的 DP 我们可以考虑合并儿子和父亲子树的信息。有如下分类讨论：

g(i,j)←∑x,y∈son(u),x≠yf(x,j−1)×f(y,j−1)g(i,j)\leftarrow \sum_{x,y \in son(u),x\neq y} f(x,j-1)\times f(y,j-1)

g(i,j)←∑x∈son(u)f(x,j−1)g(i,j)\leftarrow \sum_{x\in son(u)} f(x,j-1)

统计答案也需要分类讨论：

ans←g(i,0)ans\leftarrow g(i,0)

ans←∑x,y∈son(u),x≠yf(x,j−1)×g(y,j+1)ans\leftarrow \sum_{x,y \in son(u),x\neq y} f(x,j-1)\times g(y,j+1)

时间复杂度经优化后达到O(n)O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int MN=3e6+15;
int n;
ll buf[MN],ans,*f[MN],*g[MN],*now;
vector<int> adj[MN];

namespace Tree{
    int dep[MN],mxdep[MN],len[MN],fa[MN],hson[MN];

    void dfs1(int u,int pre){
        fa[u]=pre;
        dep[u]=mxdep[u]=dep[pre]+1;
        for(auto v:adj[u]){
            if(v==pre) continue;
            dfs1(v,u);
            if(mxdep[u]<mxdep[v]){
                mxdep[u]=mxdep[v];
                hson[u]=v;
            }
        }
        len[u]=mxdep[u]-dep[u]+1;
    }

    void dfs3(int u,int pre){
        if(hson[u]){
            f[hson[u]]=f[u]+1;
            g[hson[u]]=g[u]-1;
            dfs3(hson[u],u);
        }
        f[u][0]=1;
        ans+=g[u][0];
        for(auto v:adj[u]){
            if(v==pre||v==hson[u]) continue;
            f[v]=now;
            now+=len[v]<<1;
            g[v]=now;
            now+=len[v]<<1;
            dfs3(v,u);
            for(int i=0;i<len[v];i++){
                if(i){
                    ans+=f[u][i-1]*g[v][i];
                }
                ans+=g[u][i+1]*f[v][i];
            }
            for(int i=0;i<len[v];i++){
                g[u][i+1]+=f[u][i+1]*f[v][i];
                if(i) g[u][i-1]+=g[v][i];
                f[u][i+1]+=f[v][i];
            }
        }
    }

}using namespace Tree;

int main(){
    cin>>n;
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs1(1,0);
    now=buf;
    f[1]=now;
    now+=len[1]<<1;
    g[1]=now;
    now+=len[1]<<1;
    dfs3(1,0);
    cout<<ans;

    return 0;
}

P3441 [POI2006]MET-Subway

形式化题面如下：

给定一棵有nn 个节点的无向树和一个整数kk，选出最多kk 条不分叉的路径（即简单链），使得这些路径覆盖的不同节点数尽可能多。输出最多能覆盖的节点数。

DP 显然不太好，考虑贪心，那么贪心尽量让链长。考虑直径一定作为答案的一部分出现，而剩下的就是直径上的分支，分支跨直径配对成路径。考虑这个如何配对，其实就是不同链的叶子两两配对，考虑以直径一端点为根，长链剖分加排序（链长大到小）取2L−12L-1 个叶子即可。

实现丑了会卡常，请大家注意常数和空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<bits/stdc++.h>
#define pir pair<int,int>
using namespace std;
constexpr int MN=1e6+1520;
int n,L,rt,ftot,ans;
pir lvf[MN];
bool vis[MN];
int hd[MN],nxt[MN<<1],to[MN<<1],tot;
void add(int u,int v){to[++tot]=v,nxt[tot]=hd[u],hd[u]=tot;}

namespace ZJTree{
    struct Node{int u,fa,len;};
    int bfs(int st){
        queue<Node> q;
        int ans1=-1e9,ans2=1;
        q.push({st,0,0});
        while(!q.empty()){
            auto [u,fa,w]=q.front();q.pop();
            if(w>ans1) ans1=w,ans2=u;
            for(int i=hd[u];i;i=nxt[i]){
                int v=to[i];
                if(v==fa) continue;
                q.push({v,u,w+1});
            }
        }
        return ans2;
    }
}

namespace Tree{
    int dep[MN],fa[MN],mxdep[MN],htop[MN],len[MN],hson[MN];
    void dfs1(int u,int pre){
        fa[u]=pre;
        dep[u]=mxdep[u]=dep[pre]+1;
        for(int i=hd[u];i;i=nxt[i]){
            int v=to[i];
            if(v==pre) continue;
            dfs1(v,u);
            if(mxdep[u]<mxdep[v]) mxdep[u]=mxdep[v],hson[u]=v;
        }
        len[u]=mxdep[u]-dep[u]+1;
    }
    void dfs2(int u,int ltop){
        htop[u]=ltop;
        if(!hson[u]){lvf[++ftot]=pir(len[htop[u]],u);return;}
        dfs2(hson[u],ltop);
        for(int i=hd[u];i;i=nxt[i]){
            int v=to[i];
            if(v==fa[u]||v==hson[u]) continue;
            dfs2(v,v);
        }
    }
}using namespace Tree;

bool cmp(pir x,pir y){return x.first>y.first;}

int main(){
    read(n,L);
    for(int i=1,u,v;i<n;i++) read(u,v),add(u,v),add(v,u);
    rt=ZJTree::bfs(1);
    dfs1(rt,0);
    dfs2(rt,rt);
    sort(lvf+1,lvf+1+ftot,cmp);
    for(int i=1;i<=(L<<1)-1;i++){
        if(i==1) vis[rt]=1,ans+=len[rt];
        else{
            int p=lvf[i].second;
            while(!vis[htop[p]]) vis[htop[p]]=1,ans+=len[htop[p]],p=fa[htop[p]];
        }
    }
    put(ans);
    return 0;
}