Kruskal重构树学习笔记
1.算法简介
我们回忆一下 Kruskal 求最小生成树的过程,可以表述为以下:
- 将边按照边权从小到大进行排序。
- 若当前边 两端不连通,我们就在生成树的边集中加入这条边并连接,关于连通性显然我们可以考虑利用冰茶几维护。
有的时候,我们可能想要求得信息就和边权的大小关系有关,例如路径上的最大边权和最小边权,你可能会想到使用最小生成树,但是问题在于最小生成树上的边权是乱序的,但是我们发现在构建的最小生成树的过程就可以解决这个路径上最大边权和最小边权问题。
如果能用某种结构描述每条边被连接的先后顺序就很好了,因为越往后加入的边权就越大,就可以快速刻画边权有限制的图连通性了。
于是我们就有了 Kruskal 重构树!它在 Kruskal 的过程上进行了一些改进:
- 将边按照边权进行排序。
- 若当前边 两端不连通,连接 的时候找到 的代表元。新建节点,将并查集中 的父亲设为 ,并在图上连边 和 。注意 可能不是原树节点。
- 通常将 的权值 设置为边的边权,为虚点设置权值方便解题,巧妙设置点权对解题有极大帮助。
如果图是联通的,如上操作将会得到一颗大小为 且以 为根的二叉树,这个就是 kruskal 重构树。
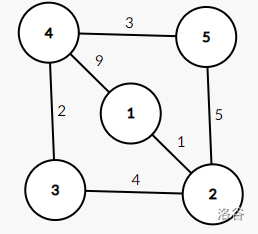
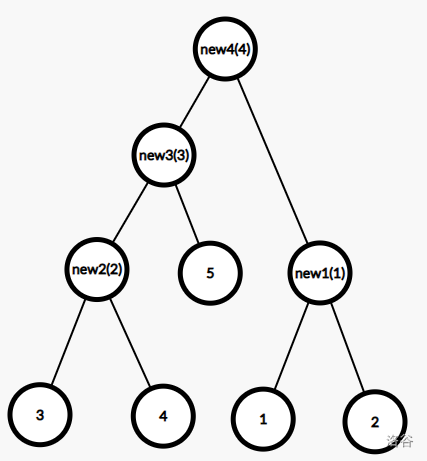
以下为例子,原图:
Kruskal 重构树:
以下为构建代码:
1 | struct Edge{ |
Kruskal 重构树有一些优秀的性质:
- 重构树是一颗二叉树。
- 原图 中所有叶子是重构树 的叶子,原节点和重构树叶子节点本质相同。
- 对于任意新节点 及其祖先,满足,默认叶子。
第三个性质是十分重要,我们在做题的时候将会重复利用该性质,它的推论:原节点 在原图上经过权值 的边可到达的所有点就是它在重构树上,最浅的祖先 满足权值 的子树内所有叶子节点。翻译下就是从一个叶子节点 倍增找到满足权值 的最浅祖先,那么 子树内所有叶子就是原图仅保留边权 的边时 所在连通块的所有点。
进一步的,原图中两个点间所有路径上的边最大权值的最小值 = 最小生成树上两点简单路径的边最大权值 = Kruskal 重构树上两点 LCA 的点权。
综上我们可以总结出一个套路,当题目限制涉及只经过权值不大于某个值的点或边的时候,我们可以从 Kruskal 的角度入手。如果我们想要利用这个刻画图连通性,我们可以通过利用可持久化冰茶几来实现动态图连通性的刻画,我们会在例题中详细说明其应用。
2. 例题
最小瓶颈路
建立 Kruskal 重构树,那么答案就是 A 点与 B 点 LCA 的点权,因为至少要满足图联通必须从 LCA 开始往上,显然不可能再往上走不然点权会更大,所以必定是 LCA。
P4197 Peaks
上面性质的拓展应用,先建立 Kruskal 重构树,每次询问找到 祖先中点权 的最浅祖先,那么答案就是子树中叶子节点点权第 大,用主席树维护即可。
[AGC002D] Stamp Rally
翻译全部错误 666.
最大编号尽可能小,考虑二分。问题转化为求经过边编号 的 路径上点数量,将边权设置为边的编号,那么命题关系求两点路径最大权值最小值,容易想到 Kruskal 重构树,且这题限制了经过点的个数要恰好为 ,不能大也不能小,所以二分是一个比较好的解决方案。时间复杂度。
P3684 [CERC2016] 机棚障碍 Hangar Hurdles
先考虑我们初始点最大能放多少,由于是一个正方形,我们考虑前缀和预处理这个网格图,然后二分求出最大长度。这样我们就能得出每一个点所能容纳的最大正方形长度。利用这个 我们对于正方形每一个点向四周连边,边权设置为,那么命题转化为求起点到终点的路径上边的权值最小值的最大值,用 Kruskal 重构树即可解决,但是为题在于连边过多,我们考虑对于 相同的点缩点即可,时间复杂度。在实现细节方面,我们注意到,由于障碍的存在,所以可能最后得到的是森林而不是一棵树。考虑到树与树之间是不连通的,所以我们完全可以新建一个节点连向这些树,并把点权设为 0,就可以直接按照普通一棵树的情况来做了。
码力题不写。
AT_arc098_d [ARC098F] Donation
牛牛牛
首先不难发现一个性质就是如果我们在某个地方给塞钱了之后我们肯定之后就不回来这里。同时发现答案必定,考虑到给钱很难想,正难则反考虑倒着走领钱,设,不难发现题目的条件就是要求满足到达点 的时候满足,如果不满足就补充即可。如果是第一次经过令。
这玩意怎么做?考虑最小生成树,令边权为,表示经过这条边当前钱数的最小值。但是我们发现这玩意很难搞,因为边权是乱序的,如果暴力枚举起点走的话是 的,但是我们发现我们肯定是贪心的走边权最小的。考虑这玩意我们可以在建树的时候求得,考虑 Kruskal 重构树表述建树这一过程。然后再树上 DP,设 表示 子树内都经过后最小领到的前,叶子节点即为,对于非叶子节点枚举从哪里最后进入出来即可,有。其中 表示 为根的子树内节点的,由于重构树显然是二叉树可以直接展开,但是如果你写多叉树那我没啥好说的,时间复杂度。
借助 Kruskal 重构树,通过合理的赋值边权我们可以满足题目中的限制,难点就是在于我们如何发掘边权所表示的意义。
CF1628E Groceries in Meteor Town
首先看到简单路径上求经过边权最大值不难想到利用 Kruskal 重构树,查询操作就转化成了重构树上, 点与所有关键点的 lca 的权值。
那么现在为题转化为如何求一个点集合的 LCA,如果你做过树上查询你可能会以为是区间 LCA 直接一个一个维护,但是显然不是这样的,这是点集不是区间。答案是点集中 dfn 最大点和 dfn 最小点的 lca,所以直接维护区间最大最小 DFN 即可。
P4899 [IOI 2018] werewolf 狼人
我做这个题的时候那一天是血月。
上下界重构树,我们考虑建两颗重构树,A 树非根节点大于父节点,B 树非根节点小于父节点。
那么我们考虑利用性质,首先再 A 树种找到,倍增跳到 满足最浅祖先。则 可以只通过编号 的点所能到的点的集合是 的子树内所有点的集合,令为。同理我们可以得到 只经过编号 的点所能到的点的集合,问题转化为求是否有解即为这两个集合是否公共点,用 DFN 主席树求解交集即可。