卡特兰数与反射容斥

0. 前言

本文章介绍内容难度不超过提高组难度，属于笔者提高组复习计划的一部分。

1. 卡特兰数

1.1 介绍

卡特兰数作为广泛出现在OI中的一类特殊数列，第$i$ 项改为$C_{i}$，其拥有广泛的意义。数列的前几项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862。

这些特殊的数字，在信息学竞赛里许多题目都有这个数列的存在，可以在打表找规律时激发灵感。

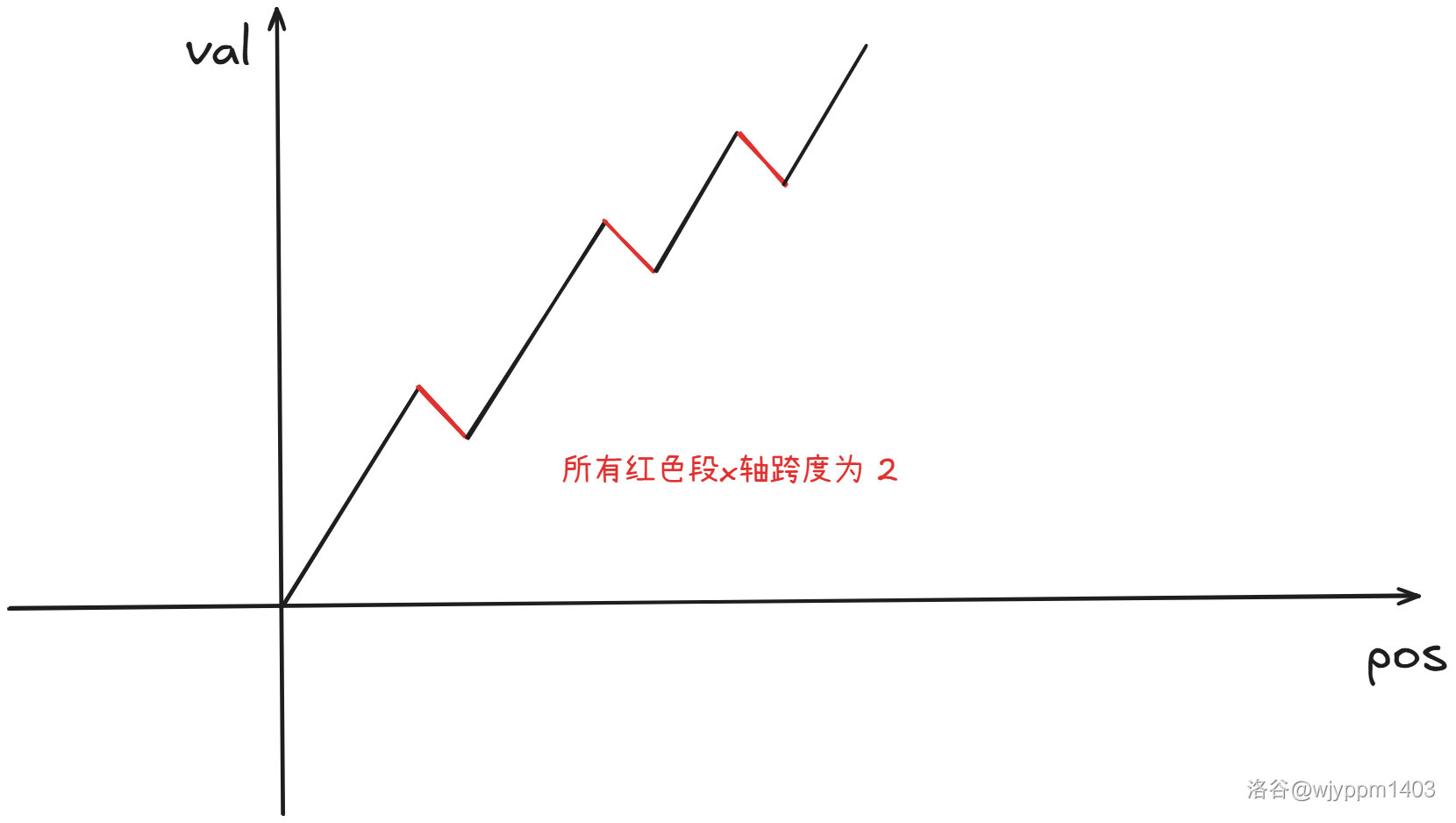
我们通过一个经典例子来说明，即折线问题，如下图：

在平面上从$(0,0)$ 走到$(n,n)$，每次只能向上或者向右走，不穿过 $y=x$ 这条直线有多少种方案。

1.2 朴素解法

我们考虑枚举最后一个$y=x$ 上的点$(i,i)$，可以把问题规模缩小。

我们强制钦定最后一段不碰到$y=x$，我们在$(i,i)$ 继续向终点走去的过程中，第一步只能向右走，到$(n,n)$ 的最后一步只能向上走，中间的问题我们可以视作从$(i,i+1)\to (n,n-1)$ 不穿过$y=(x-1)$ 的直线方案数，平移有：

中间这段答案就是$C_{n-i-1}$，故可以求出$C_{n}=\sum\limits_{i=0}^{n-1} C_{i}C_{n-i-1}$。
在众多卡特兰数所对应的题目如出栈顺序，括号匹配中，缩小问题规模是一个很经典的做法。

但是这样的时间复杂度为$O(n^2)$，我们考虑能否得到一个$O(n)$ 或者$O(1)$ 的过程。

1.3 容斥解法

本解法请仔细理解，因为会涉及到第二章的讲解。

正难则反，我们考虑用所有路径数减去不合法路径的数量。总的是$\dbinom{2n}{n}$，我们思考不合法路径的数量，考虑把一条不合法路径进行操作： 把一条不合法路径在第一次触碰到$y=x+1$ 的这条线的点设为$p$，我们在 $p$ 右侧的在$y=x+1$ 以下的部分全部沿 对称到上方，我们发现这样翻转之后，所有可能出现的不合法路径，和$(0,0)\to (n-1,n+1)$ 的路径产生了一一映射的关系。

所以我们就有$C_{n}=\dbinom{2n}{n}-\dbinom{2n}{n-1}=\dfrac{1}{n+1}\dbinom{2n}{n}$。

1.4 总结与经典应用

$C_{n}$ 共两个公式，一个$C_{n}=\sum\limits_{i=0}^{n-1} C_{i}C_{n-i-1}$，一个$C_{n}=\dbinom{2n}{n}-\dbinom{2n}{n-1}=\dfrac{1}{n+1}\dbinom{2n}{n}$。

一些等价模型：

• 由$n$ 对左右括号构成的合法的括号序列数。
• 栈（无穷大）的进栈序列$\{1,2,\dots,n-1,n\}$ 由多少个不同的出栈顺序。
• $n$ 个$1$ 和$n$ 个$-1$ 构成$2n$ 项$a_1,a_2,\dots,a_{n}$ 的任意前缀和$\ge 0$ 的序列数量个数。
• $n$ 个节点可以构造出多少个不同的二叉树。
• 圆上选择$2n$ 个点，将这些点成对连接起来使得所得到的$n$ 条线段不相交的方法数？

有经验的不难发现前四个性质是完全一致的，而最后一个可以进一步推论。

而卡特兰数计数的本质，是任何前缀中总存在某种约束的不可逆平衡（如左括号数$\ge$ 右括号数）。

1.5 例题

例题是多的，这里举例几个经典应用。

P2532 [AHOI2012] 树屋阶梯

我们思考要求强制使用$n$ 个举行有没有什么特殊性质，我们发现一个矩形，其左下角这个矩形，一定右上角是某个拐点，否则我们会发现，我们需要额外使用一个矩形去覆盖这个拐点。

那么我们可以缩小问题规模，每次对这个阶梯状物，进行一个枚举覆盖左下角这个矩形的右上角是哪一个拐点，不妨设为第$x$ 个拐点，那么上面就是一个$x-1$ 的子问题，下面为$n-x-1$ 的子问题，不难发现答案就是$C_{n}=\sum\limits_{i=0}^{n-1} C_{i}C_{n-i-1}$，即卡特兰数。

P3978 [TJOI2015] 概率论

期望是困难的，我们直接考虑统计$n$ 个点可能的二叉树数量$f_{n}$ 和其叶子总数$g_{n}$。注意到$f_n$ 就是卡特兰数，而$g_{n}$ 如何计算呢？打表发现$g_{n}=nf_{n-1}$，证明太长了不想过多证明（逃）。

答案就是$\dfrac{g_n}{f_n}=\dfrac{n(n+1)}{4n-2}$。

P4769 [NOI2018] 冒泡排序

众所周知的是，冒泡排序的交换次数就是排列的逆序对数。

首先不考虑字典序（即特殊性质），我们如何计算有多少个排列满足逆序对数等于$\dfrac{1}{2} \sum\limits_{i=1}^n |i-p_{i}|$。我们考虑原式子为$cnt=\dfrac{1}{2} \sum\limits_{i=1}^n |i-p_{i}|$，变形有$2\cdot cnt=\sum\limits_{i=1}^n |i-p_{i}|$，其中后面的式子我们考虑用图论刻画，即$i\to p_{i}$ 进行连边，那么$|i-p_{i}|$ 就表示跨过的距离，那么合法当且仅当每条边穿过的格子正好对应它参与的逆序对的个数，即所有逆序对两两配对成边的端点，且没有多余交叉。

也就是说，逆序对必须两两配对，不可能出现一个位置被两个人抢走配对的情况。

等价的转化提议，即不存在三元即以上的序列满足$i<j<k$ 使$p_{i}>p_{j}>p_{k}$。即不存在三元即以上的下降子序列。

那么这样如何刻画呢？我们发现这玩意由于没有一元子序列这一说法，那么必定为二元下降子序列，我们用图来表示合法序列数变化这一过程：

我们发现拐点必然是当前时刻序列的最大值然后接一个较小值，然后再继续上升。

故有一个 DP，设$f(i,j)$ 表示前$i$ 个数构成的排列最大值为$j$ 的方案数，转移为$f(i,j)=f(i-1,j)+f(i,j-1)$，要求$j\le i$。这玩意是搞笑的$O(n^2)$，但是不难发现这玩意就是格路计数但是有$j\le i$ 的限制，可以转化为卡特兰数，可以$O(1)$ 计算，或者公式为$\dbinom{i+j}{i}-\dbinom{i+j}{j+1}$。

现在考虑有字典序的限制，这个限制我们可以转化为至少一个位置满足$p_{i}> q_{i}$，其余任意。我们考虑枚举法确定这个位置什么，我们钦定一个位置$i$，前面的和$q_{i}$ 一致，第$i$ 个必须大于$p_{i}$。令$mx=\max_{j=1}^{i-1} q_{j}$，$mn$ 为最小可以填的数。

由于我们强制钦定之后从$(1,1) \to (n,n)$ 的$f$ 的计算就不再适用了，我们将其定义为从$(i,j)$ 走到$(n,n)$ 的方案数。

接下来我们考虑如何计算方案数，考虑分类讨论：

• 若$p_{i}=mn$，那么我们显然只能填写$x>mx$ 的方案，即$f(i,mx+1)$。
• 若$mn<p_{i}<mx$，显然只能填写$x>mx$，但是显然这样构成不合法排列了，故无解。
• 若$p_{i}\ge mx$，只需要填写一个$x>p_{i}$ 的数就可以了，即$f(i,p_{i}+1)$。

时间复杂度$O(n)$。

2. 反射容斥

2.1 反射法介绍与卡特兰三角

有些人会将反射法叫做映射法，这里本文章称作反射法。

回看 1.3 的解法，我们通过构造$y=x+1$ 的直线，然后将终点进行对称构造双射。我们将这种通过构造直线然后对称构造的类似方案,把每一条第一次越界的坏对象反射为一个更容易计数的对象，从而用总数减去反射得到的坏数得到合法对象数。我们称作反射法。

我们来介绍一个经典应用，当然不是卡特兰数因为介绍过了，我们介绍卡特兰三角。

定义$C(n,k)$ 表示由$n$ 个$1$，$k$ 个$-1$ 构成的序列中，前缀和不小于零的序列数。说人话就是还有$y=x$ 的限制，但是是从$(0,0)$ 走到$(n,k)$。

通过上面 1.3 的方法我们当然可以构造一个直线$y=x-1$ 来构造双射：

那么原命题类似的，可以转化为从$(0,0)\to (k-1,n+1)$ 的自由路双射，原命题即为$\dbinom{n+k}{k}-\dbinom{n+k}{k-1}$。

同时不难有性质：$C(n,k)=\sum\limits_{i=0}^k C(n-1,i)=\sum\limits_{i=k}^n C(i,k-1)$。

例题：P1641 [SCOI2010] 生成字符串

2.2 双线反射容斥

而多数时候，限制条件不仅仅想卡特兰数中$y=x$ 一条直线的约数，可能是多重约数。例如纵坐标必须限定在$[0,m]$ 的范围内。换句话说，也就是不仅仅由一条死线的限制，可能有多个死线的限制，在 OI 中一般涉及到的是两个死线的问题。以下我们令两条线分别为$A:y=x+a$ 和$B:y=x+b$，默认$b<a$ 即 A 在 B 上方。

简单一点，如果限制只有一个形如$y=x+a$，终点是$(n,m)$ 那么如何满足，当然还是用我们的反射法，第一次触碰开始反转，终点就是变成关于$y=x+a$ 对称的点$(m-a,n+a)$。那么直接求解自由路即可。

简化问题做完了，我们原命题如何做，对于一条线的容斥，我们相当于去掉了所有包含 A 的串和包含 B 的串。 所以如果对两条线分别跑一次容斥，包含 AB 和 BA 这些串会被去掉两次。

我们要再把先触碰 A 再触碰 B 的方案数加回来，再把先触碰 B 再触碰 A 的方案数加回来。 然后此时包含 ABA 和 BAB 的串又被多加了一次，以此类推。显然碰线的上限次数是确定的，只需要展开有限项即可。

但是难点在于两个都经过的方案，我们考虑两个都经过的方案数怎么算

我们思考能否类似于上面的反射法，将路线反射呢，我们考虑，如果先对$y=x+a$ 翻折，然后对$y=x+(2a-b)$ 进行翻折，这个$y=x+(2a-b)$ 表示 B 直线通过 A 翻折上去后的直线，会变成：

那么方案数就可以通过组合数进行计算了。通过上述我们容斥的过程不断计算即可。注意到每一次反射至少减少一个坐标。所以我们可以在$O(\dfrac{n+m}{a+b})$ 的时间复杂度内完成这一操作。

请注意这个特殊的复杂度，这个复杂度可以和一个神秘知识点叫做根号分治结合考察。

2.3 例题

P3266 [JLOI2015] 骗我呢

骗你呢。

省流：

$f(1,0/1/2/\dots/m)=1$，$f(i,j)=\sum\limits_{k=0}^{j-1}f(i-1,k)$。
求$\sum\limits_{i=0}^m f(n,i)$，其中$n,m\le 10^6$。

先考虑改写 DP 式子，不难改写为$f(i,j)=f(i,j-1)+f(i-1,j+1)$，当$j=0$ 时$f(i,j)=f(i-1,j)+f(i-1,j+1)$。时间复杂度$O(n^2)$。

这种方程是典型的格路计数类方程，考虑将转移图画出来，发现两个移动方向，一个往左上，一个往右。坐标轴一侧变为向上和向右。考虑到左上很难搞，考虑拉伸坐标轴，将左上方向拉伸为和正上方，变为：

把左边的箭头改一改，改成往上后往右即可，根据 DP 性质不难发现两个不能经过的线：$y=x+2$ 和$y=x-(m+1)$，直接反射 DP 即可，以下为参考：

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=5e6+15,MOD=1e9+7;
int n,m,x,y,pw[MN],inv[MN],ans;

int ksm(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=ret*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return ret;
}

void flipa(){
    swap(x,y);
    x--;
    y++;
}

void flipb(){
    swap(x,y);
    x+=m+2;
    y-=m+2;
}

void initpw(){
    pw[0]=1;
    for(int i=1;i<MN;i++){
        pw[i]=pw[i-1]*i%MOD;
    }
    inv[MN-1]=ksm(pw[MN-1],MOD-2);
    for(int i=MN-2;i>=0;i--){
        inv[i]=inv[i+1]*(i+1)%MOD;
    }
}

int getC(int a,int b){
    if(a<b||b<0) return 0;
    return pw[a]*inv[b]%MOD*inv[a-b]%MOD;
}

int calc(int x,int y){
    if(x<0||y<0) return 0;
    return getC(x+y,x);
}

signed main(){
    initpw();
    cin>>n>>m;
    x=n+m+1,y=n;
    ans=calc(x,y);
    while(x>=0&&y>=0){
        flipa();
        ans=(ans-calc(x,y)+MOD)%MOD;
        flipb();
        ans=(ans+calc(x,y))%MOD;
    }
    x=n+m+1,y=n;
    while(x>=0&&y>=0){
        flipb();
        ans=(ans-calc(x,y)+MOD)%MOD;
        flipa();
        ans=(ans+calc(x,y))%MOD;
    }
    cout<<ans;
    return 0;
}

Gym 104053J

首先$i=1$ 的时候容易有$a_{1}=1$，对于$i>1$ 有：

$$\begin{aligned} 4S_{i} & =a_{i}^2+2a_{i}+1 \\ 4S_{i-1}+4a_{i}&=a_{i}^2+2a_{i}+1 \\ 4S_{i-1}&=a_{i}^2-2a_{i}+1 \\ 4S_{i-1}&=(a_{i}-1)^2 \\ \therefore a_{i}&=1\pm 2\sqrt{S_{i-1}} \end{aligned}$$

注意到$S_{i}=S_{i-1}+a_{i}=S_{i-1}\pm 2\sqrt{S_{i-1}}+1=(\sqrt{S_{i-1}}\pm 1)^2$。设$x_{i}=\sqrt{S_{i}}$，那么拆括号后会变号，那么$b_{1}=1$，$b_i=b_{i-1}=\pm 1$。

考虑值域限制：

• 若$b_{i}=b_{i-1}+1$，那么要求$a_{i}=1+2b_{i-1}=2b_{i}-1$，即$b_{i}\le \dfrac{m+1}{2}$。
• 若$b_{i}=b_{i-1}-1$，那么显然$b_{i}\ge 0$。

相当于在平面直角坐标系上每一次向右上或右下走一步，初始在$(1,1)$，走$n-1$ 步后要求纵坐标在$[0,\dfrac{m+1}{2}]$ 范围内的方案数，反射容斥即可。

CF1967E1 Again Counting Arrays

先考虑发掘一些性质：

• 每一列至多一个障碍。
• 障碍会导致方向出现三种选择情况：上下、只上、只下。不可能出现无法选择的情况，因为每一列至多一个障碍。
• 当我们走到$y=m$ 的时候无敌，因为$a_{i}\in [1,m]$，可以一直往上走。

我们考虑给定障碍的点，即给定$a$ 我们应该如何判定是否合法，有一个想法就是我们贪心的能往上走就尽量往上走到$y=m$ 的位置。因为根据性质 2 障碍只可能限制至多一个方向的前进，分类讨论不难有往上走是最优解。

我们现在有了决策，现在我们考虑如何计数上述合法的$a$。考虑 DP，注意到决策只与当前所处的最后一个位置纵坐标有关，故设$f(i,j)$ 表示决策到第$i$ 个数，最后一个的位置纵坐标为$j$ 的$a$ 方案数，转移分类讨论有：

• $f(i+1,j+1)\leftarrow (m+1)f(i,j)$；
• $f(i+1,j-1)\leftarrow f(i,j)$，当且仅当$j<m$。
• $f(i+1,m)\leftarrow f(i,m)\cdot m$。

转移是$O(nm)$ 的就很难泵，考虑优化，发现这玩意是一个$O(1)$ 递推式子，而且发现这玩意及其类似格路计数问题。考虑转化问题，我们从$(0,b_{0})$ 开始走，每次可以选择右上和右下走，我们有两个限制，一个是碰到$y=-1$ 就寄了，一个是碰到$y=m$ 的时候就结束了。显然我们不难发现这是双线限制问题，可以考虑反射容斥，但是问题在于反射容斥双线是死线是不能碰，这里出现的是一个死线一个活线。

我们可以考虑枚举结束位置$(i,m)$，在这个位置之前都不能碰到$y=m$ 不然就非法，这样就能套上反射容斥了。特别的，枚举$(n,i)$ 作为结束位置，这个时候$y=m$ 就全部都是死线。然后就可以做了，具体实现由于我不会右上右下的反射容斥，我们可以考虑反向旋转 45 度给回归到往右走和往上走，这样就可以套上 P3266 的做法了。

等会！我们还没有处理 DP 中的系数呢，首先将$(i,m)$ 和$(n,i)$ 旋转之后变为$(\frac{i-m+b_{0}}{2},\frac{i+m-b_{0}}{2}-1)$ 和$(\frac{n-i}{2},\frac{n+i}{2})$。对于$(i,m)$ 求解的我们乘上$(m-1)^{\frac{i+m-b_{0}}{2}}m^{n-i}$ 的系数，后面乘上$(m-1)^{\frac{n+i}{2}}$即可。

搞笑的，这玩意是$O(\dfrac{n^2}{m}+n)$ 的，但是注意到我们有两个做法，一个是$O(nm)$，一个是$O(\dfrac{n^2}{m}+n)$ 的，直接考虑根号分治，设定阈值$B$，满足$m\le B$ 用 DP，否则用计数，时间复杂度$O(n\sqrt{n})$。

番外：CatPTG 告诉我说不能用 P3266 的维护方法给我了个直接维护右上右下。我真信了，我调不出来然后我去自己写旋转坐标系的出来了搞笑了。

#include<bits/stdc++.h>
#define int long long
#define pir pair<int,int>
using namespace std;
constexpr int MN=5e6+15,MM=2e5+15,MOD=998244353;
int pw[MN],inv[MN],n,m,b0,ppm[MN],ppm1[MN];

int ksm(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=ret*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return ret;
}

void initpw(){
    pw[0]=1;
    for(int i=1;i<MN;i++){
        pw[i]=pw[i-1]*i%MOD;
    }
    inv[MN-1]=ksm(pw[MN-1],MOD-2);
    for(int i=MN-2;i>=0;i--){
        inv[i]=inv[i+1]*(i+1)%MOD;
    }
}

int getC(int a,int b){
    if(a<b||b<0) return 0;
    return pw[a]*inv[b]%MOD*inv[a-b]%MOD;
}

namespace SUB1{ //dp 要开滚动数组
    constexpr int MQ=3520;
    int f[2][MQ],ret;

    void init(){
        ret=0;
        for(int i=0;i<=m;i++){
            f[0][i]=0;
        }
    }

    void initdp(int f[]){
        for(int i=0;i<=m;i++) f[i]=0;
    }

    int solve(){
        init();
        f[0][b0]=1;
        int now=0,nxt=1;
        for(int i=0;i<n;i++,nxt^=1,now^=1){
            initdp(f[nxt]);
            for(int j=0;j<m;j++){
                if(!f[now][j]) continue;
                if(j){
                    f[nxt][j-1]=(f[nxt][j-1]+f[now][j])%MOD;
                }
                if(j+1<m){
                    f[nxt][j+1]=(f[nxt][j+1]+f[now][j])%MOD;
                }else ret=(ret+f[now][j]%MOD*(m-1)%MOD*ppm[n-i-1]%MOD*ppm1[(i+j-b0)/2]%MOD)%MOD;//这里应该时 ppm[n-i] ppm1[(i+j-b0-1)]，但是因为 i 从 0 开始枚举的搞笑了
            }
        }
        for(int i=0;i<m;i++){
            if(f[now][i]){
                ret=(ret+f[now][i]*ppm1[(i+n-b0)/2]%MOD)%MOD;// 同理
            }
        }
        return ret;
    }

}

namespace SUB2{ // rong chi

    void flip(pir &x,int k){
        swap(x.first,x.second);
        x.first-=k;
        x.second+=k;
    }

    int calc(pir x){
        if(x.first<0||x.second<0) return 0;
        return getC(x.first+x.second,x.first);
    }

    int sol(int x,int y,int fl,int fr){ 
        // from (0,0) to (x,y),y must in [fl,fr]
        // maybe fl>fr,But this is reflective inclusion-exclusion,I don't care ¯\_(ツ)_/¯
        pir pos=pir(x,y);
        int ret=calc(pos);
        while(pos.first>=0&&pos.second>=0){
            flip(pos,fl);
            ret=(ret-calc(pos)+MOD)%MOD;
            flip(pos,fr);
            ret=(ret+calc(pos))%MOD;
        }
        pos=pir(x,y);
        while(pos.first>=0&&pos.second>=0){
            flip(pos,fr);
            ret=(ret-calc(pos)+MOD)%MOD;
            flip(pos,fl);
            ret=(ret+calc(pos))%MOD;
        }
        return ret;
    }

    int solve(){
        int x=b0,y=0,ret=ksm(m,n);
        for(int i=b0;i<n;i+=2,x++,y++){
            ret=(ret-sol(x,y,m-b0,-1-b0)*ppm[n-i-1]%MOD*ppm1[y]%MOD+MOD)%MOD;
        }
        return ret;
    }

}

void init(){
    ppm[0]=ppm1[0]=1;
    for(int i=1;i<=n;i++){
        ppm[i]=ppm[i-1]*m%MOD;
        ppm1[i]=ppm1[i-1]*(m-1)%MOD;
    }
}

void solve(){
    cin>>n>>m>>b0;
    if(b0>=m){
        cout<<ksm(m,n)<<'\n';
        return;
    }
    init();
    if(m*m<=n){
        cout<<SUB1::solve()<<'\n';
    }else cout<<SUB2::solve()<<'\n';
}

signed main(){
    initpw();
    int T;
    cin>>T;
    while(T--){
        solve();
    }


    return 0;
}

2.4 一点小感想

反射容斥源于卡特兰数的组合意义技巧，即我们一开始说的反射法。是反射法和容斥法的有机结合，更多地运用了容斥思想，用满足部分条件的集合的交并刻画我们 需要的集合。

在遇到有限制的格路计数问题中，我们可以通过反射容斥来进行操作。

至于 Dyck 路，先咕咕咕吧。

3. 参考

图源：

• 第一章图出处：浅谈卡特兰数 - fhq_treap 和我。
• 2.1 图出处：StayAlone 的文章。
• 2.2 图出处：格路计数和反射容斥 - OIer某罗

参考：

• 浅谈卡特兰数 - fhq_treap。
• StayAlone 的文章。
• 格路计数和反射容斥 - OIer某罗
• 格路计数与反射容斥 - yzy4090