CF573D题解
好题。
有一个显然的想法就就是二分图带权最大匹配，但是时间复杂度是 及其难受，考虑 DP 但直接 DP 十分困难，考虑发掘一些性质。
利用贪心思想，先对 和 进行从小到大的排序，一个基本思想就是对应位置的相乘，用调整法不难证明这是最优决策，但是本题目中存在第 个人不能骑自己的马，所以最优解可能不会取到。
考虑到这个限制只是限制自己不能骑自己的马，合理猜测 位置匹配马的决策是一个范围，有结论：匹配范围为。证明考虑反证法，设 的禁止匹配位置为。那么反证法，假设如果在这个以外的范围选，那么最多向前会造成两次 无法匹配，自行画图发现这种情况最劣情况下也只会在 的情况形成匹配。
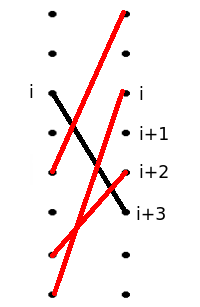
借用 _sys的图：
完美匹配至少有三个红线和黑线相交整法不难证明如果两条线相交那么交换这两个匹配会得到更优的解。
让后考虑交换的过程，我们如果前 个人和前 匹马匹配完全，那么存在， 这区间内的人和马匹配，可以用反证法证明。
故，设 表示前 个人和前 匹马完成匹配的最大全职，所以从 转移过来即可，同时改成矩阵方式维护 DP 做动态 DP 即可，时间复杂度，其中 是矩阵带来的常数。
相关推荐
2025-08-10
2025-8-10提高组模拟赛
被诈骗的一集。 话说你是打得好才记吗，下次打的不好更应该记录反思的好吧。 T1 CF1295D Same GCDs - 洛谷 暴力肯定是不行的，考虑如何对这个 xxx 计数，考虑算术唯一分解定理，对于 gcd\gcdgcd 来说就是所有质数上指数取 min\minmin，那么对 gcd(a+x,m)=gcd(a,m)\gcd(a+x,m)=\gcd(a,m)gcd(a+x,m)=gcd(a,m) 可以把 xxx 以质因数分解的形式看待的话，就是加上 xxx 之后取 min\minmin 的值不变，可以分析出几个性质： xxx 不会添加新的质数，质数取集只在 a,ma,ma,m 之间。 xxx 不会改变 aaa 取到 min\minmin 指数的质数贡献。 那么有 gcd(x,m)=gcd(a,m)\gcd(x,m)=\gcd(a,m)gcd(x,m)=gcd(a,m)，除掉 gcd(a,m)\gcd(a,m)gcd(a,m)，gcd(xgcd(a,m),mgcd(a,m))=1\gcd(\frac{x}{\gcd(a,m)},\frac{m}{\gc...
2025-08-16
2025.8.16模拟赛
T1 8 数码问题简化版，O(7!)O(7!)O(7!) 爆搜 BFS，没了。 T2 ∑i=0m+1(n+1i)=∑i=0m(ni)+(n−1i)\sum\limits_{i=0}^{m+1}\binom{n+1}{i}=\sum\limits_{i=0}^{m}\binom{n}{i}+\binom{n-1}{i} i=0∑m+1(in+1)=i=0∑m(in)+(in−1) ∑i=0m+1(ni)=∑i=0m(ni)+(nm+1)\sum\limits_{i=0}^{m+1}\binom{n}{i}=\sum\limits_{i=0}^m \binom{n}{i}+\binom{n}{m+1} i=0∑m+1(in)=i=0∑m(in)+(m+1n) 时间复杂度为 O(n)O(n)O(n)，瓶颈在预处理组合数。 T3 Subtask 1 暴力枚举排列，逆序对也可以暴力统计，时间复杂度 O(7!)O(7!)O(7!)。 Subtask 2 注意到暴力枚举排列不行，但是注意到这个只和排列奇偶性有关。本质上就是求行列式。具体的就是照题目的把矩阵 [...
2025-08-14
20250814模拟赛
前言 省流：300 分。 T1 考虑 DP，设 f(i,0/1/2)f(i,0/1/2)f(i,0/1/2) 表示处理到第 iii 个数，当前是往左，不动，往右，方案是否合法，转移如下： f[i][0]=f[i−1][0]⋅[xi−xi−1=1]+f[i−1][1]⋅[xi−(xi−1−1)=1]+f[i−1][2]⋅[xi−(xi−1+1)=1],f[i][1]=f[i−1][0]⋅[xi−1−xi−1=1]+f[i−1][1]⋅[xi−1−(xi−1−1)=1]+f[i−1][2]⋅[xi−1−(xi−1+1)=1],f[i][2]=f[i−1][0]⋅[xi+1−xi−1=1]+f[i−1][1]⋅[xi+1−(xi−1−1)=1]+f[i−1][2]⋅[xi+1−(xi−1+1)=1],\begin{aligned} f[i][0] &= f[i-1][0] \cdot [x_i - x_{i-1} = 1] + f[i-1][1] \cdot [x_i - (x_{i-1} - 1) = 1] + f[i-1][2] \c...
2025-06-10
ABC236G题解
推销自己的矩阵优化文章：矩阵快速幂优化DP 注意到点数及其小，边数也算小，而 LLL 极大，有一股浓烈的矩阵快速幂优化的味道。 首先这个问题肯定是一个 DP 的题，我们有一个暴力的想法，我们对于每一个操作，利用 Floyd 的 DP 思想，邻接矩表示图两点之间经过 111 条边的路径数量这个特点，对于每一个操作我们更新邻接矩阵，让后在上面跑矩阵快速幂，幂 LLL 次后的邻接矩阵代表的就是经过 LLL 条边的信息，一次次更新答案判断可达性即可，时间复杂度 O(Tn3logL)O(T n^3 \log L)O(Tn3logL)，不能通过。 我们考虑如何优化，根据题意，每一次操作只会添加一条边，而要求的是求经过边中操作编号更靠后（也就是更大）的边。我们可以将这个操作编号绑到边权上，那么实际上我们就是要对经过的边的边权取 max\maxmax 操作。 那么我们有一个显而易见的状态，设 f(i,j,k)f(i,j,k)f(i,j,k) 表示在从 iii 到 jjj 节点，经过 kkk 条边的最大边权，转移如下： f(i,j,k)=min{maxp=1nf(i,p,k−1)+w(p...
2025-06-15
ABC410E题解
可能更洛谷的体验 有一个 O(n3)O(n^3)O(n3) 的 DP 是很显然的，就是设 f(i,j,k,0/1)f(i,j,k,0/1)f(i,j,k,0/1) 表示第 iii 只怪兽，用了 jjj 的体力，用了 kkk 的魔力，当前打怪兽用不用魔力的最大打怪兽数量，这显然不能通过。 我们考虑什么状态中信息是有用的。首先，既然我们是一个一个按顺序打的怪物，遇到每一个怪兽我们肯定都要打。那么实际上我们根本就不用存储打怪兽的数量，只需要存储当前魔力或体力的信息，通过这个我们来判断是否到现在能够打怪兽。 那么，我们只需要把体力或魔力任一维度丢到我们 DP 求解的答案即可，因为这里我们有一个是否使用魔力的状态决策，我们考虑把魔力丢进去。 设 f(i,j,0/1)f(i,j,0/1)f(i,j,0/1) 表示第 iii 只怪兽，用了 jjj 的体力，当前打怪兽用不用魔力的最小魔力使用。转移方程是显然的： f(i,j,0)=min{f(i−1,j+ai,0),f(i−1,j+ai,1)}f(i,j,1)=min{f(i−1,j,0),f(i−1,j,1)}+bi\begin{align...
2025-08-08
CF1474F题解
头脑风暴！ 注意到 xxx 对答案一点用都没有，因为我们求的是长度，光一个 ddd 就能够确定答案了。 发现最长严格上升子序列的性质不太好刻画，我们考虑这个添加数的操作过程能不能以一种形式来表现出来。注意到每一个数具体取值只和最后一个数的变化有关，而且变化是连续的，考虑给它拍到二维平面上，横轴按照每一次添加一个数划分时间，纵轴为最后一个值的具体取值，原操作在二维平面上表现的是斜率为 1 或 -1 的一堆直线，如下图，红点表示一次插入操作的： 最长严格上升子序列的性质就很好刻画了，因为根据图来看其实就是最低点和最高点的极差就是我们的长度（因为斜率为 ±1\pm 1±1）。让后我们考虑这个子序列个数怎么解决。发现直接 DP 求解答案十分困难，考虑发掘性质，首先不难发现一个性质：一个段不可能贡献超过一种答案，即一个点不可能成为最低点或最高点。 这个性质有什么用呢，也就是说，我们可以统计对段的答案进行贡献统计。然而注意到段数极小（数据范围 nnn），值域极大，有一个强烈的矩阵味道，但是我到现在连状态都没设计耶？ 最长严格上升子序列可能从任意值拼过来，考虑在状态中加上这一个，设 f(i,...
评论
