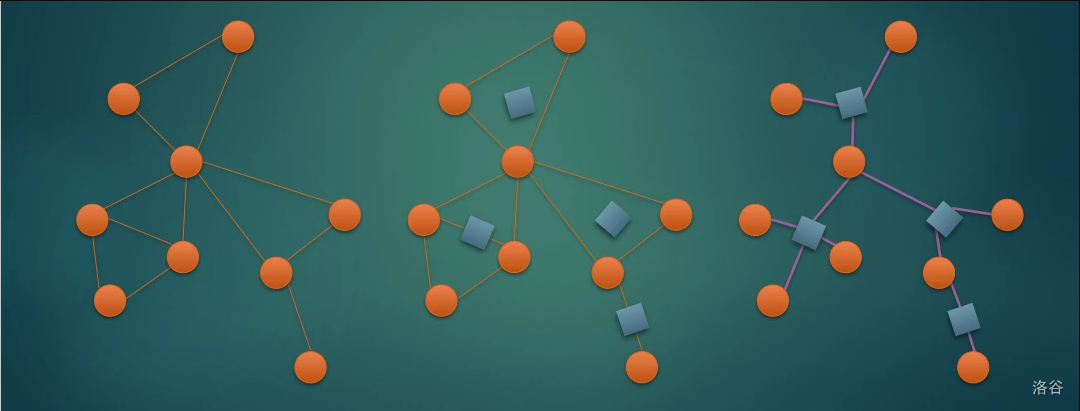
广义圆方树
0. 前言
我们主要讨论的就是广义的圆方树。
1. 介绍
广义圆方树是刻画图上点连通性的工具,是 Tarjan 算法的一个强有力拓展。广义圆方树能够述原图任意两点之间的所有割点,即路径 上所有必须经过的点。下面有一张图来举例:
图的问题我们不好处理,但是众所周知,树上问题是比普通的图论问题处理起来方便得多的。所以我们将图转化为圆方树的意义就是在于通过树上的算法简化问题。
广义圆方树中的节点分为两类:圆点和方点,在上图中所表示出来。圆点就是原本图上的点,而每个方点都代表了一个点双联通分量。将每个方点和所有在这个联通分量中的点连起来。
注意,只有原图联通的时候才能是一棵树,如果不连通的话那么会形成森林。
我们在求解点双的时候可以顺便建出圆方树,以下为代码, 为原图, 为圆方树。
1 |
|
2. 例题
在说明例题之前,完全有必要说明一个结论:
若在圆方树上 是 的必经点,则原图 是 的必经点,且为割点。
P4630
考虑两圆点在圆方树上的简单路径,与路径上经过的方点相邻的圆点的集合,即为原图此简单路径上的点集。
对于题目中三元组,考虑固定,求 的数量。答案就是 之间简单路径并集的数量减去 2。
我们考虑如何用圆方树实习这一过程,这里有一个圆方树的 Trick:在路径统计时,给点附上合适的点权。
本题中,我们方点赋权为点双大小,而圆点赋值为 -1,这样问题转化为了统计圆方树上两圆点之间简单路径权值和,时间复杂度是 的,无法通过,考虑优化。我们考虑把贡献分摊到每个点上,每个点对答案的贡献就是通过他的路径条数乘上它的权值,而路径条数围为: (所有以此点为根的树中每两个子树中圆点个数相乘再相加,再加上每个子树中圆点个数与不属于这个点的树的圆点个数相乘)。
也可以用换根 DP 解决,时间复杂度都是。
P4606 战略游戏
扣掉这个节点后 不能到达,说明该点为 路径上的一个必经点,转化一下题意就是割点。考虑建广义圆方树,那么原题转化为求点集 的虚树上不包含属于 的圆点数量。每次统计虚树上的点数即可,复杂度。
如果你不想建虚树,不妨考虑做树上距离前缀和即可。
P4334
考虑建广义圆方树。
- 第二问:即判断圆方树两点路径上是否存在点,可以用树剖解决。
- 具体的,我们在树刨求 的时候,跳深度大的点 的时候,若 和当前要跳的点 在一条链上并且深度比 小,那么存在。否则一直判断,直到 在同一链上的时候(仍令),判断 和 是否在一条链上并且 即可。
- 第一问:首先判断 是否为割边(对应到圆方树就是点双大小为 2),若是,则判断其对应的方点是否在路径上,问题转化为第二问。
时间复杂度。
P3225 矿场搭建
以下 为图的点数。
并非板子,考虑题目希望我们给出一种选择关键点的方式,满足删去任何一个点后形成的每个连通块内都存在至少一个关键点。
非割点是没有营养的,割点是十分有的,那么命题等价为删掉任意一个割点之后连通块存在关键点。
考虑最好情况,整个图是点双连通分量,那么答案就是。
考虑不是,那么注意到是和割点有关的信息,考虑建出广义圆方树。让后我们要对这个圆方树进行一些小操作,即把所有叶子都给删掉,即原图的非割点,我们得到了广义圆方树的由原图割点和点双方点构成的树。
我们在这颗树上搞事情,那么命题相当于在上面任意删掉一个圆点,连通块存在关键点。有一个方案就是将这颗树的叶子(即叶子方点)放一个关键点,证明这个方案是最少的。反证法可以证明。
那么令叶子对应点双大小为,那么若第一问答案为,第二问的答案就是。
CF487E
点赋权与树分治 Trick 应用。
在 的简单路径上当且仅当 和 某个方点相邻,令方点的权值为对应点双所有节点对应权值最小值,将圆方树树剖求路径最小值即可回答询问。
但是有修改哎,怎么办,修改点权时可能影响到很多方点权值,无法承受。我们可以考虑类似于树分治的思想,只维护儿子的信息,我们将方点维护一个 multiset,里面存所有与之相邻的圆点权值,然后权值就是 multiset 中的最小值,修改圆点权值时修改其父节点的 multiset 并更新其父节点权值。
同理求点权最小值即可,时间复杂度。
P8456
好题,但是做这个题的时候脑子特别困,浪费了这个题了呜呜呜。
先建出圆方树,那么原命题可以分类讨论成两种情况:在一个点双和不在一个点双。
- 在一个点双:如何点双里面所有颜色都相同那么就完蛋了。如果两种颜色都有的话,你可能和我一样点双内部点都合法,但是分析一下发现不是这样。例如一个二元环,但有
d和D的边,就炸杠了。考虑这个反例会对答案如何贡献,发现这个反例有且仅有一个,也就是说如果一个点双里有且只有两个点满足其既有 D 也有 d 的出边,那么其对答案的贡献就是,否则贡献的就是。 - 不在一个点双:我们把点双分类:全
d点双,全D点双,混合点双。论是如果两点在圆方树上的路径上全是黑点双,或者全是白点双的时候才不合法。证明见 Alex_weiのSolution
实现上我们容斥,不合法的首先有形如同色点双构成的极大同色连通块,可以通过圆方树上 dp 求解贡献,再对每个非同色点双看看是否要减去一对 u,v 的贡献即可。